2019-数据结构-数据结构7.0-排序
排序
1. 概述
- 排序:n个对象的序列R[0],R[1],R[2],…R[n-1] 按其关键码的大小,进行由小到大(非递减)或由大到小(非递增)的次序重新排序的。
- 关键码(key):进行排序的根据
- 两大类:
- 内排序:对内存中的n个对象进行排序。
- 外排序:内存放不下,还要使用外存的排序。(在本节中暂不考虑)
- 排序算法的稳定性:如果待排序的对象序列中,含有多个关键码值相等的对象,用某种方法排序后,这些对象的相对次序不变的,则是稳定的,否则为不稳定的。例: 35 81 20 15 82 28 81 82 15 20 28 35 稳定的
- 排序种类
- 内排序
- 插入排序,交换排序,选择排序,归并排序,基数排序
- 外排序:本章暂不讨论外排序
- 内排序
- 排序的算法分析
- 时间开销 — 比较次数,移动次数
- 所需的附加空间 - 空间开销
- 下面是静态排序过程中所用到的数据表类定义:

1.1. 排序算法类定义
1 | |
2. 插入排序
- 排好前面两个,然后在后面的部分进行插入排序。
- 思想:思想:V0,V1,…,i-1个对象已排好序,现要插入Vi到适当位置
- 例子:体育课迟到的人
- 方法:直接插入排序,链表插入排序,折半插入排序,希尔排序
2.1. 直接插入排序
2.1.1. 直接插入排序源码
1 | |
- 比较的时候是从后向前比较的。
- 合并后的插入排序
1 | |
1 | |
2.1.2. 算法复杂度分析

- 额外的两次移动来自于a[i]的取出和放回,除此以外在最坏的情况下会每一次比较都会进行比较。



2.1.3. 算法稳定性
稳定的
2.2. 折半插入排序(Binary Insert Sort)
- 又称为折半查找

2.2.1. 源码
1 | |
1 | |
2.2.2. 时间复杂度


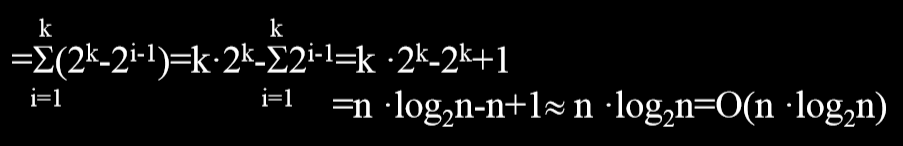
2.2.3. 折半插入排序稳定性
算法是稳定的
2.3. 希尔排序(Shell Sort)
- 又称缩小增量排序(diminishing - increament sort)
- 方法:
- 取一增量(间隔gap < n),按增量分组,对每组使用 直接插入排序或其他方法进行排序。
- 减少增量(分的组减少,但每组记录增多)。直至增量为1,即为一个组时。
- 例子:
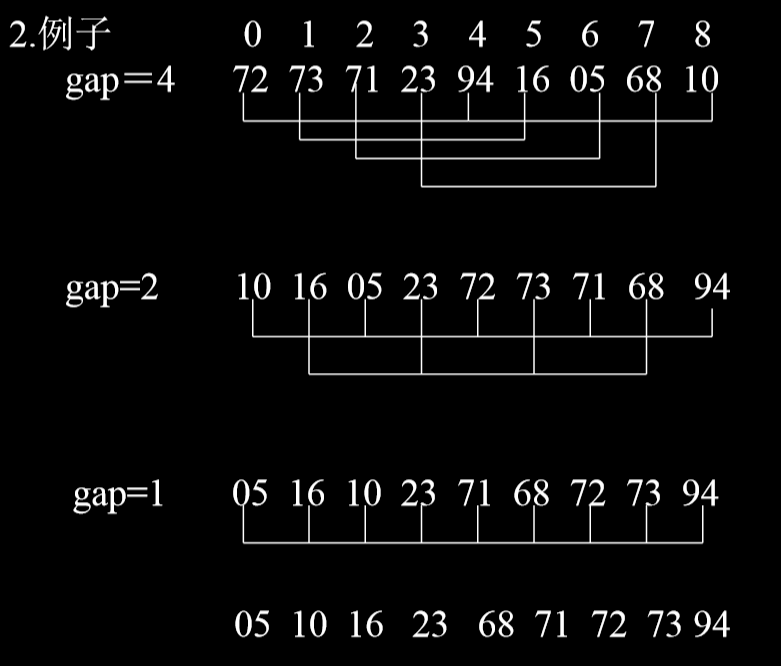
- 每次完成排序后,gap每次都取一半。
2.3.1. 希尔排序的代码实现
1 | |
1 | |
2.3.2. 希尔排序的稳定性
不稳定的
2.3.3. 希尔排序算法分析
- 与选择的缩小增量有关,但到目前还不知如何选择最好结果的缩小增量序列。
- 平均比较次数与移动次数大约n1.3左右
3. 交换排序(一类排序算法)
- 方法的本质:不断的交换反序的对偶,直到不再有反序的对偶为止。
- 两种方法:
- 冒泡排序(Bubble sort)
- 快速排序(Quick sort)
3.1. 冒泡排序
- 每次遍历一次数组,然后仅仅比较相邻的两个数字,最坏的情况时每次只能讲一个数字冒泡上去。
- 然后遍历n次
3.1.1. 源码
1 | |
1 | |
3.1.2. 冒泡排序算法分析
- 进行几次元素之间的比较?
- 从n-1开始往下比较
- 进行了几次元素之间的交换
- 不确定
3.1.3. 冒泡排序算法的稳定性
稳定的
3.1.4. 冒泡排序算法复杂度分析
- 最小比较次数
- 有序:n-1次比较,移动次数为0
- 最大比较次数
- 逆序:(n-1)+(n-2)+…+1=n(n-1)/2 约等于 O(n2) (比较次数)
移动次数 = 3*(1+2+3+…+n)=(3/2)n(n-1) i=1 (移动次数)
- 逆序:(n-1)+(n-2)+…+1=n(n-1)/2 约等于 O(n2) (比较次数)
3.2. 快速排序
3.2.1. 算法内容
- 在n个对象中,取一个对象(如第一个对象——基准pivot),按该对象的关键码
- 把所有小于等于该关键码的对象分划在它的左边。
- 大于该关键码的对象分划在它的右边。
- 对左边和右边(子序列)分别再用快速排序。
3.2.2. 例子

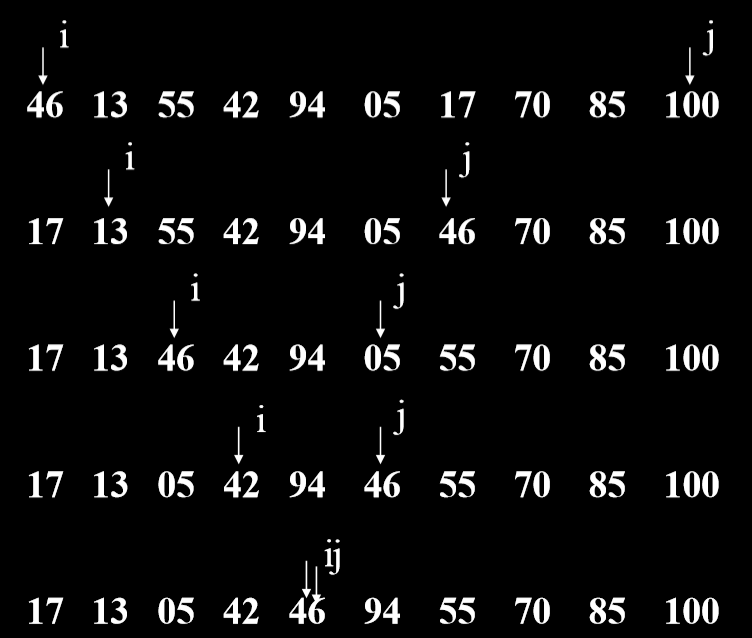
3.2.3. 算法实现
1 | |
java实现
1 | |
3.2.4. 快速排序算法的稳定性
不稳定的排序方法
3.2.5. 快速排序的时间复杂度
- 最差的情况(当选第一个对象为分划对象时) 如果原对象已按关键码排好序,此时为O(n2)
1 | |
- 最理想的情况:每次分划第一个对象定位在中间
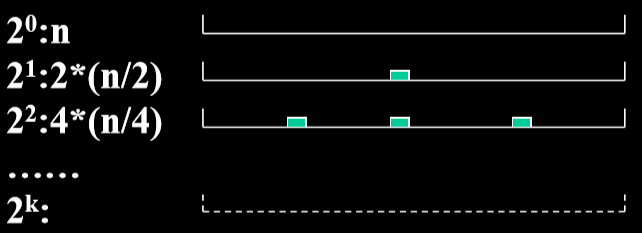
- 平均情况:设n=2k,一共做了K趟 K=log2n T(n) <= n+2T(n/2) <= n+2(n/2+2T(n/4))=2n+22T(n/22) <= 2n+22(n/22+2T(n/23))=3n+23T(n/23) <= … <= kn+2kT(n/2k)=nlog2n+nT(1)=O(nlog2n)
可以证明Quicksort的平均计算时间也是O(nlog2n)
3.2.6. 空间复杂度
- 以上讨论的是递归算法,也可用非递归算法来实现。 不管是递归(由编译程序来实现)还是非递归。第一次分划后,左部、右部要分别处理。
- 优先使用左侧小端部分,之后就可以释放
- 存放什么:左部或右部的上、下界的下标。
- 栈要多大:O(log2n)- O(n)(有序情况)
3.2.7. 快速排序避免有序情况
- 选取pivot(枢纽元)用第一个元素作pivot是不太好的。
- 方法1:随机选取pivot, 但随机数的生成一般是昂贵的。
- 方法2:三数中值分割法(Median-of-Three partitioning) N个数,最好选第(N/2)(向上取整)个最大数,这是最好的中值,但这是很困难的。一般选左端、右端和中心位置上的三个元素的中值作为枢纽元。
- 8, 1, 4, 9, 6, 3, 5, 2, 7, 0 (8, 6, 0)
- 具体实现时:将 8,6,0 先排序,即 0, 1, 4, 9, 6, 3, 5, 2 , 7, 8, 得到中值pivot为 6
- 分割策略:
- 将pivot与最后倒数第二个元素交换,使得pivot离开要被分割的数据段。然后,i 指向第一个元素,j 指向倒数第二个元素。
- 0, 1, 4, 9, 7, 3, 5, 2, 6, 8
- 然后进行分划
- 将pivot与最后倒数第二个元素交换,使得pivot离开要被分割的数据段。然后,i 指向第一个元素,j 指向倒数第二个元素。
- 三数中值分隔法
3.2.8. 参考
4. 选择排序
- 每次找到数组中的最小值找到然后放到前面,进行重复递归。
- 也可以将最大的数字找出来然后当放到后面。
4.1. 直接选择排序
- 思想:首先在n个记录中选出关键码最小(最大)的 记录,然后与第一个记录(最后第n个记录)交换位置,再在其余的n-1个记录中选关键码 最小(最大)的记录,然后与第二个记录(第n-1个记录)交换位置,直至选择了n-1个记录。
4.1.1. 源码
1 | |
1 | |
4.1.2. 直接排序算法内容分析

- 一次swap操作中包含3次子操作。
- 以上均是对于元素操作的统计
4.1.3. 直接排序时间复杂度

4.1.4. 直接排序稳定性
不稳定的
4.2. 锦标赛排序
- 直接选择排序存在重复做比较的情况,锦标赛 排序克服了这一缺点。
- 具体方法:
- n个对象的关键码两两比较得到(n/2)(向上取整)个 比较的优胜 者(关键码小者)保留下来, 再对这(n/2)(向上取整)个对象再进行关键码的两两比较, ……直至选出一个最小的关键码为止。如果n不是2的K次幂,则让叶结点数补足到满足 2k < n <= 2k个。
- 输出最小关键码。再进行调整:即把叶子结点上,该最小关键码改为最大值后,再进行 由底向上的比较,直至找到一个最小的关键码(即次小关 键码)为止。重复2,直至把关键码排好序。
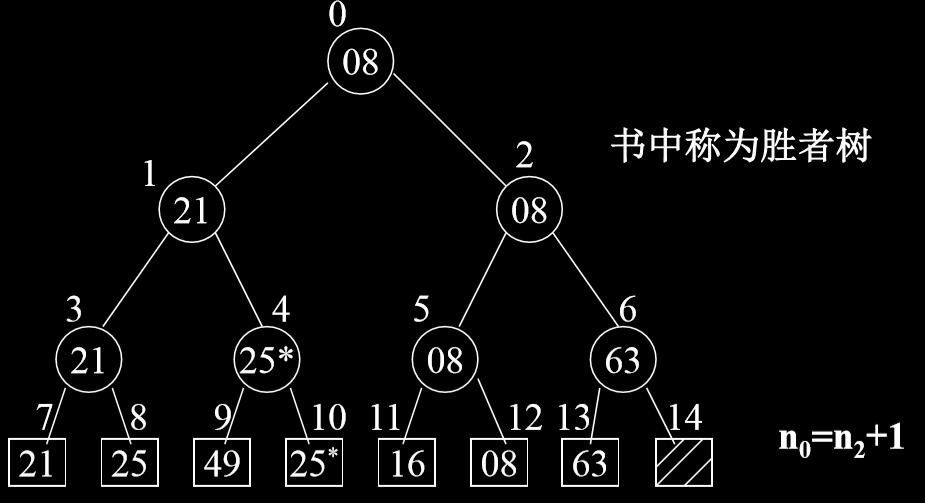
4.2.1. 锦标赛排序的算法分析

4.3. 堆排序
- 参考heap部分
- 是固定的算法,从小到大排序,所以一开始建立最大堆,最后调整为最小堆
- 不稳定的
4.3.1. 算法思想
- 第一步,建堆,根据初始输入数据,利用 堆的调整算法FilterDown(),形成初始堆。(形成最大堆)
- 第二步,一系列的对象交换和重新调整堆
4.3.2. 示例
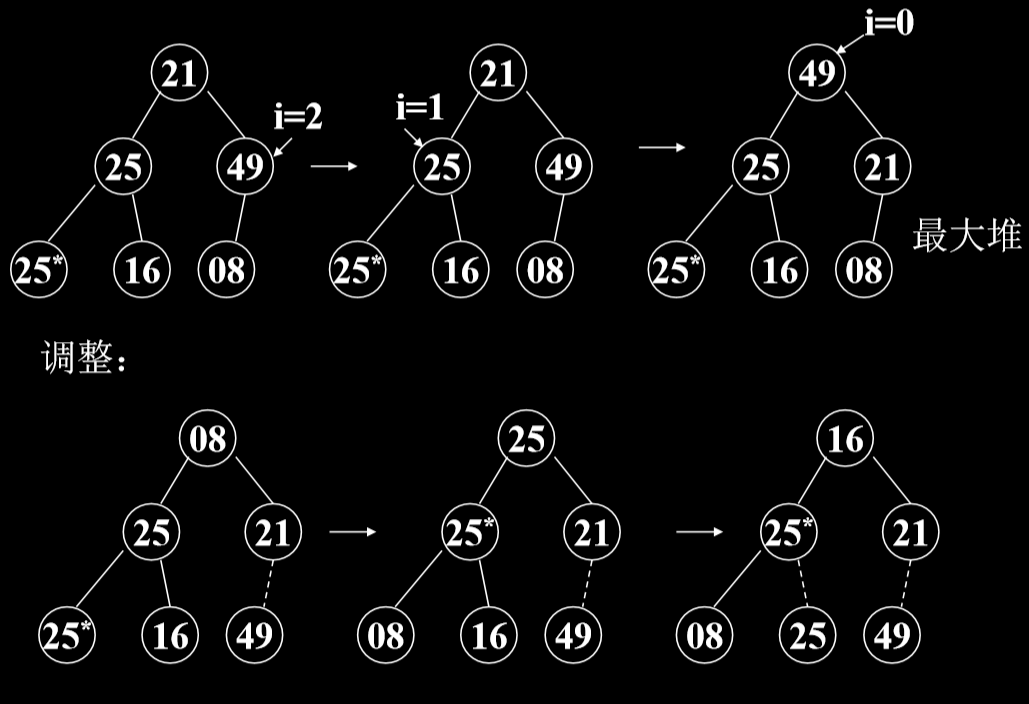
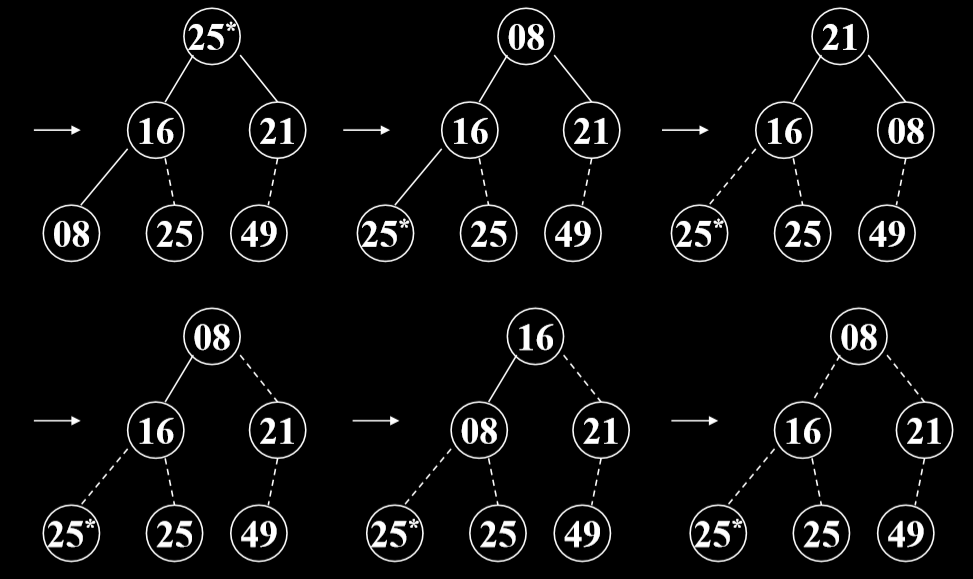
4.3.3. 代码实现
1 | |
- FilterDown()就是第6章中的,但要改一下:那里是 建最小堆,这里是建最大堆。
1 | |
4.3.4. 堆排序算法复杂度分析

5. 秩排序(Rank sort)
- 重新启用一个数组,用来记录相应的排名
5.1. 源码
1 | |
5.2. 秩排序算法性能分析
- a中元素的比较次数:1+…+n-1
- a中元素的交换次数:2(n-1-i)
- 由于while的迭代次数不定,所以很难从代码层面确定次数
- 从问题本身出发,最多调用2n次交换
6. 基数排序(Radix Sort)
- 先取个位数,按照个位数来放到十个桶里面。
- 根据先后次序进图桶
- 按照十位数,继续放入桶中,根据个位排序结果
- 重复上述操作,直到最高位。
- 原理:每次让这一位的从前往后排序。


7. 归并排序
- 归并:两个(多个)有序的文件组合成一个有序文件 方法:每次取出两个序列中的小的元素输出之;当一序列完,则输出另一序列的剩余部分

- 算法思想:分而治之(分治思想)
7.1. 代码实现
1 | |
7.2. 归并排序
- 方法
- n个长为1的对象两两合并,得n/2个长为2的文件
- n/2个长为 2………………….得n/4个长为4的文件…
- 2个长为n/2的对象两两合并,得1个长为n的文件
7.2.1. 例子

7.2.2. 非递归算法c++代码实现
1 | |
- 当两段均满len长时调用merge
- 当一长一短时也调用merge(但第二段的参数不同)
- 当只有一段时,则复抄
- 块合并算法实现
1 | |
- 算法分析:合并趟数log2n,每趟比较n次,所以为O(nlog2n)
- 稳定性:稳定。
7.2.3. 递归算法java实现
1 | |
7.2.4. 算法分析
- 合并趟数log2n,每趟比较n次,所以为O(nlog2n)
7.2.5. 算法稳定性
- 稳定性:稳定。
7.3. 递归的表归并排序
- 使用静态链表的方法来实现

7.3.1. 算法实现
- 主程序 mergesort(L)
- 子程序 divide(L,L1),将L划分成两个子表 3.合并两有序序列 merge(L,L1)
1 | |
7.3.2. 有序链表的merge算法
1 | |
7.3.3. 下面讨论divide(List&L1,ListL2)
- 将L1表分为两个长度几乎相等的表,L1.first指向前半部分,L2.first指向后半部分,要求被划分的表至少含有两个结点。

- 方法:设两个流动指针p,q指向表的结点 一般来讲让p前进一步,q前进二步,最后当q= NULL时,这时p 恰好指向前半张表的最后一个结点。
- Eg.如果有10个结点,p走5次,q走10次正好走到表末尾
1 | |
8. 总结
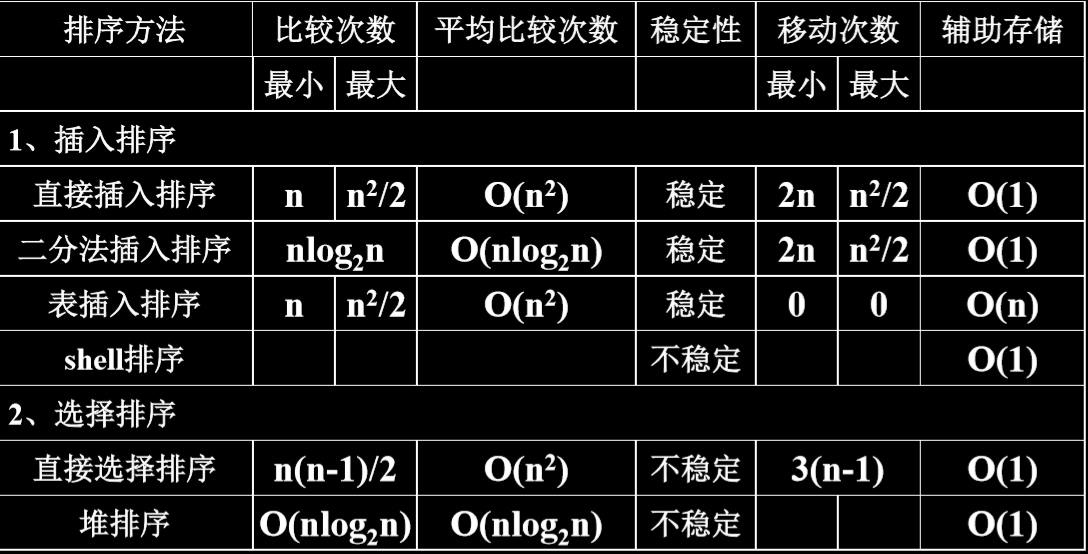

9. 例题
- 若数据元素序列 11, 12, 13, 7, 8, 9, 23, 4, 5 是采用下列排序方法之一得到的第二趟排序后的结果, 则该排序算法只能是 A. 起泡排序 B. 插入排序 C. 选择排序 D. 二路归并排序
- 首先不是冒泡排序:最大最小值上下,选择排序也是选择最大最小,答案是B
2019-数据结构-数据结构7.0-排序
https://spricoder.github.io/2020/01/17/2019-Data-Structure/2019-Data-Structure-%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%847.0-%E6%8E%92%E5%BA%8F/