2019-计算机组织与结构-lecture06

Floating-point Arithmetic

1. 对于浮点数而言，乘除是比较简单的，但是加减是困难。

1. Float类型变量的表示

1.1. 浮点数表示的定义

1.2. 浮点数的表示方法

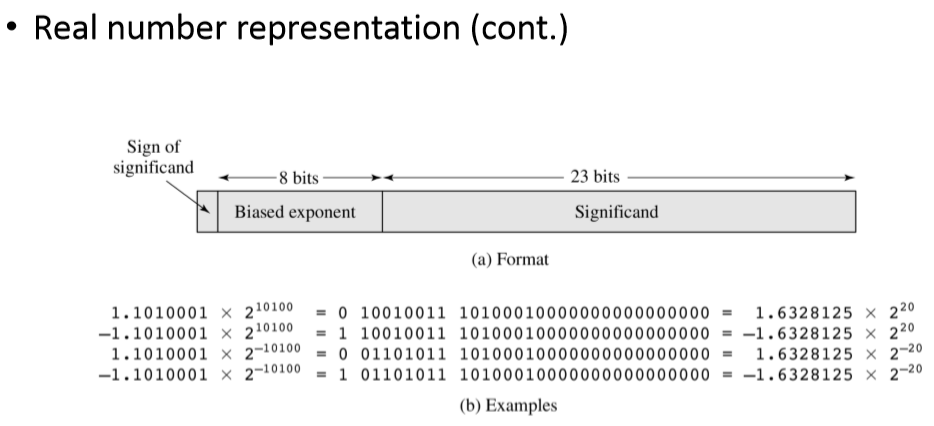
1.3. 浮点数的表示

1.4. 浮点数的表示范围

2. 加减运算

1. 加减首先要想办法把两个小数点对齐
2. 对齐方式:一定是小的向大的靠近，而不是大的向小的部分靠近。
   • 我们怕的是向大的调整会出现上溢。

2.1. 加减的过程

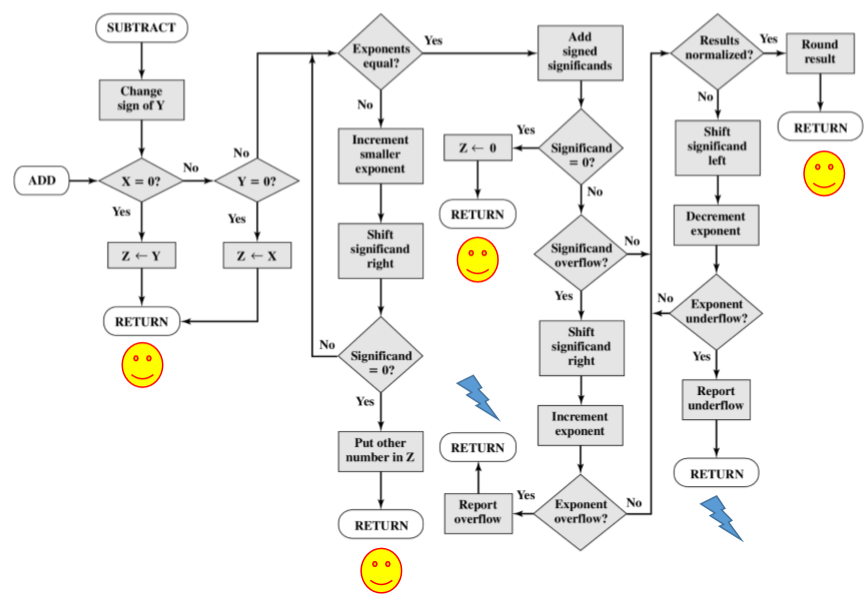
1. Add signed significands：表示需要根据正负号来进行运算，如果是正号那么直接加，如果是负号，那么进行减法。
   • 参与运算的尾数是64位，而不是32位。
2. 发现尾数是0，我们判断他是0，我们需要把它的指数设置为0，在进行加法运算后，如果是两个相反数相加，那么需要将指数位清0。
3. significand是尾数。

2.2. 问题出现

2.3. 尾数溢出

1. 如果1.00…0加上1.00…0进位，那么我们需要右移指数自加。

2.4. 指数溢出

1. 如果溢出，我们要把s设为全0,指数变化为全1(E=127,E是减去127后的)

2.5. 结果规格化

1. 将s左移，保证规格化(当两个数字很接近的时候)
   • 1.11111-1.11110
2. 问题出现:
   • 如果减法过于接近的话，结果可能降低到2^-127以下
   • 反规格化时，便表示过小，指数退1(-126和-127，也该是s/2)，也就是1.00…0转换成0.00…0这样子

2.6. 关键步骤:带符号的数字如何直接相加？

1. 加法的时候，我们只要把符号拿出来相加，然后后面相加即可
2. 减法的时候，我们可以先借位。(X-Y=X+2-Y-2)
   • 2 = 1.11…1 +0.00…1
   • 先借位2，然后如果产生进位，那么直接还掉2即可
   • 如果不够减，那么最后仍需要进行取反加一，然后在前面添加一个负号，和之前的(X-Y)整体外面的部分的符号作用。

2.6.1. 几个例子

1. 减法要借位，最后要确定能不能还上

2.7. 减法的例子

1. 符号不同
2. 第二个右移指数为变大，将缺省的数字添加起来
   • 1.00…00 + 0.11100…0
   • 绿色部分的第一个数字是缺省位

2.8. 加法的例子

1. 对齐后进行有符号整数的相加
2. 就是首先对齐指数位，下面变成0 111000…0,然后有符号整数相加，先取反加一为1 001000…0
3. 接下来可以之后，我们需要进行规格化，因为比较小。
4. 减法需要借位，最后进行判断。

3. 乘除运算

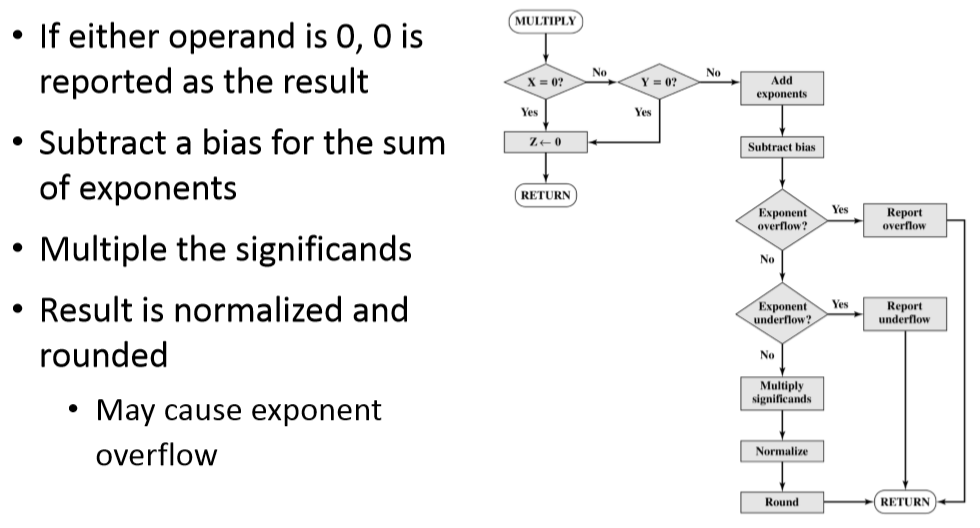
1. 首先我们进行异或运算
2. X*Y = (a₁异或a₂) s₁*s₂*2^e₁+e₂
   • e₁ = E₁ - 127
   • e₂ = E₂ - 127
   • E₁ + E₂ - 127 = E_* = e₁ + e₂ + 127

3. 接下来s₁*s₂
   • 小数点应该在第一个后面
   • 减去了127
4. 左侧是指数位运算，也就是指数一+指数二-127

4. 除法运算

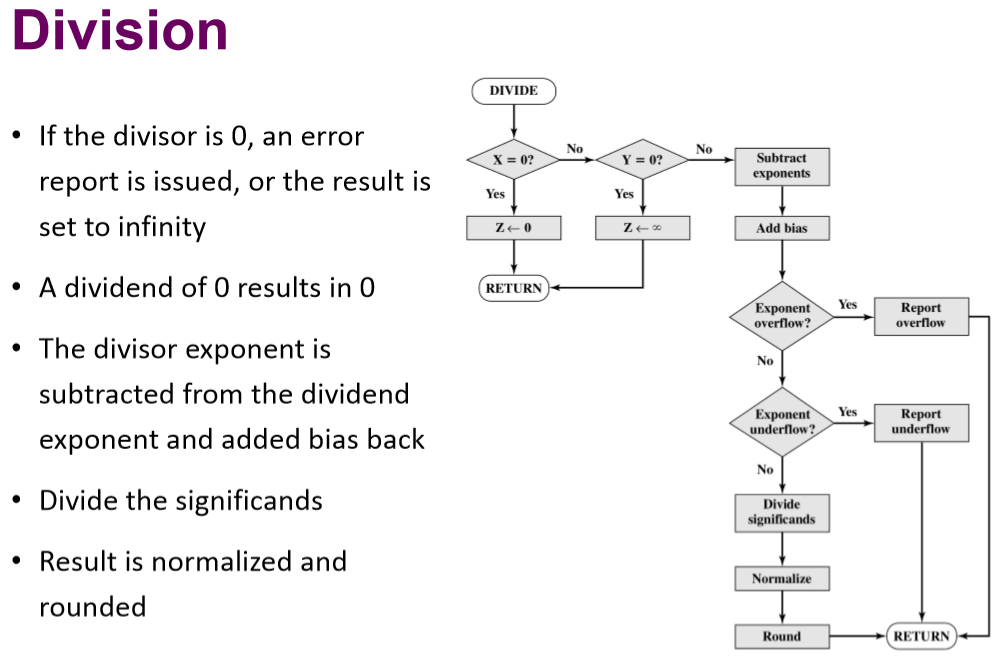
1. 同样127会被减去，所以需要加回来，在调整指数的时候

5. 浮点数的精度问题

1. 有一些数字是不能被准确正好的表示的。
2. y比x小2^-23。
3. 在运算过程中1会被丢掉
   • 首先对齐，那么y的整体会下移，然后最后一位的1被丢掉了
   • 相当于表示精度的位数刚好被丢掉了
4. 问题产生了，那么我们怎么去解决呢？我们使用guard bits也就是扩展到28位存储，防止精度丢失
   • guard bits:保护位

5.1. Rounding

1. 我们有了保护位，但是之后的保护位被舍去的时候，我们怎么处理保护位中仍存在的部分呢？
2. 我们可以直接截取:总体来说这个数字是向0靠近

5.1.1. 舍弃策略

1. 向正无穷:负数尾数全部截，正数尾数进位
2. 向负无穷:正数尾数全部截，负数尾数进位
3. 向0靠近
4. 四舍五入:
   1. 最后4位，如果第一位是0，那么直接截去。
   2. 最后4位。如果第一位是1，那么我们产生进位。

5.1.2. 问题来了:保护位用没有可能让你运算的结果更加不正确

5.2. 接下来我们进行分别计算

5.3. 加法

1. 保护位6位，因为一共16位，符号为1位，数字9位
2. 如果用四舍五入就没问题了
3. 为什么有了保护位，精度反而下降了？
   • 保护位保护的是652.0和7.4765625这里面的数字，而未必是原来数字的精度