2020-编译原理-Semantics1-概述

Semantics1-概述

1. 属性文法(Attribute Grammar)

属性文法(Attribute Grammar):为上下文无关文法赋予语义

1. 一对概念
2. 两类属性定义
3. 三种实现方式
4. 四大应用

1.1. 关键问题: 如何基于上下文无关文法做上下文相关分析?

语法分析树上的有序信息流动

1.2. 表达式求值

1. 类型系统(语义分析)
2. 抽象语法树
3. 后缀表达式(中间代码生成)

1.3. 语法制导定义(Syntax-Directed Definition; SDD)

1. SDD是一个上下文无关文法和属性及规则的结合。
2. 每个文法符号都可以关联多个属性

3. 每个产生式都可以关联一组规则
4. SDD唯一确定了语法分析树上每个非终结符节点的属性值
5. SDD没有规定以什么方式、什么顺序计算这些属性值
6. 计算使用SDT(Syntax-Directed Translation)

1.4. 注释(annotated)语法分析树

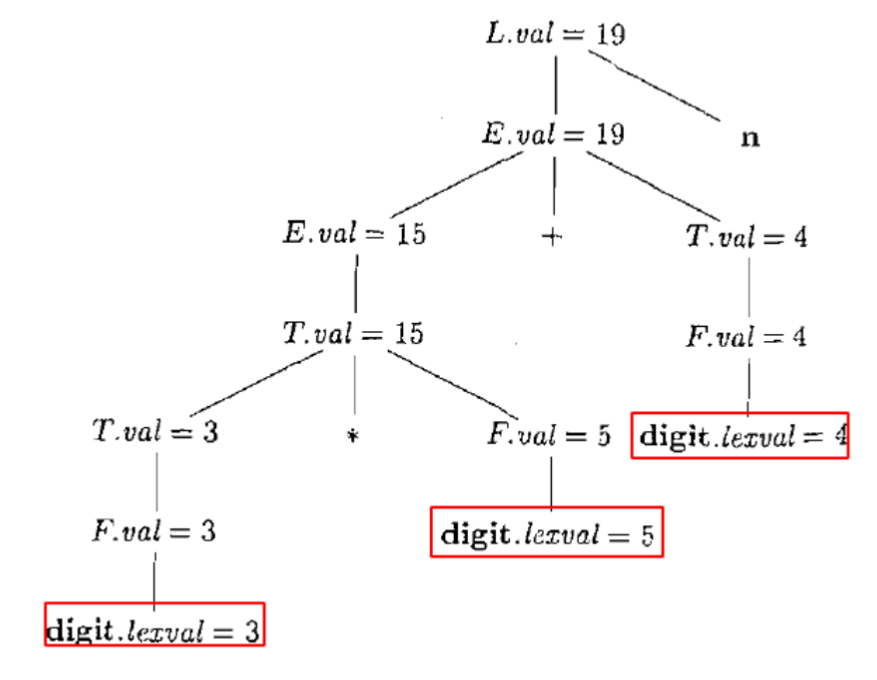
1. 显示了各个属性值的语法分析树：3 ∗ 5 + 4
2. 添加属性/值得到的就是注释语法分析树

1.5. Definition(综合属性(Synthesized Attribute))

1. 节点N上的综合属性只能通过N的子节点或N本身的属性来定义。
2. 直观上就是要么能被子节点计算得到，要么是自身持有。

1.6. Definition(S属性定义(S-Attributed Definition))

1. 如果一个SDD的每个属性都是综合属性,则它是S属性定义。

1.6.1. 依赖图用于确定一棵给定的语法分析树中各个属性实例之间的依赖关系

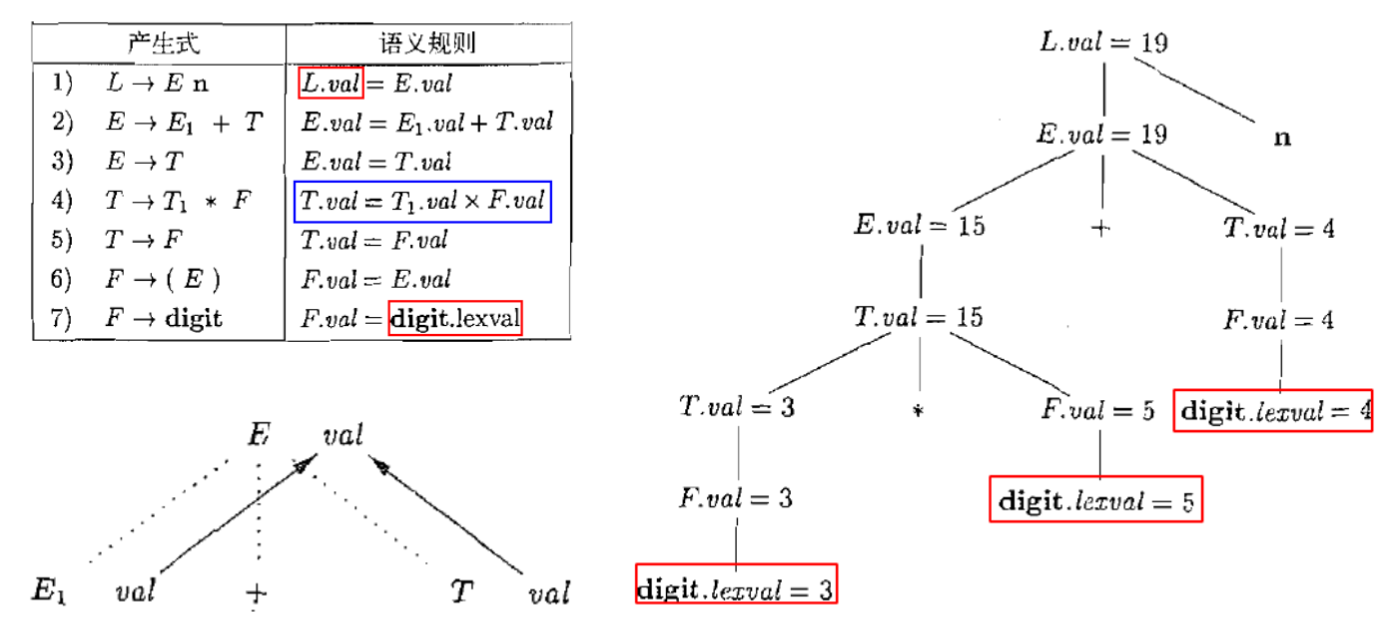
1. S属性定义的依赖图描述了属性实例之间自底向上的信息流。
2. 因此,此类属性值的计算可以自然地在自底向上的语法分析过程中实现
3. 当LR语法分析器进行归约时,计算相应节点的综合属性值
4. 此类属性值的计算也可以在自顶向下的语法分析过程中实现
5. 在LL语法分析器中,递归下降函数A返回时,计算相应节点A的综合属性值，逐渐计算即可。
6. 全部是综合属性的话，计算是冗余的

1.6.2. T’有一个综合属性syn与一个继承属性inh

红色边框的部分是集成属性，比如A?B:C

1.6.3. Definition (继承属性(Inherited Attribute))

1. 节点N上的继承属性只能通过N的父节点、N本身和N的兄弟节点上的属性来定义。

1.6.4. 继承属性T’.inh用于从左向右传递中间计算结果

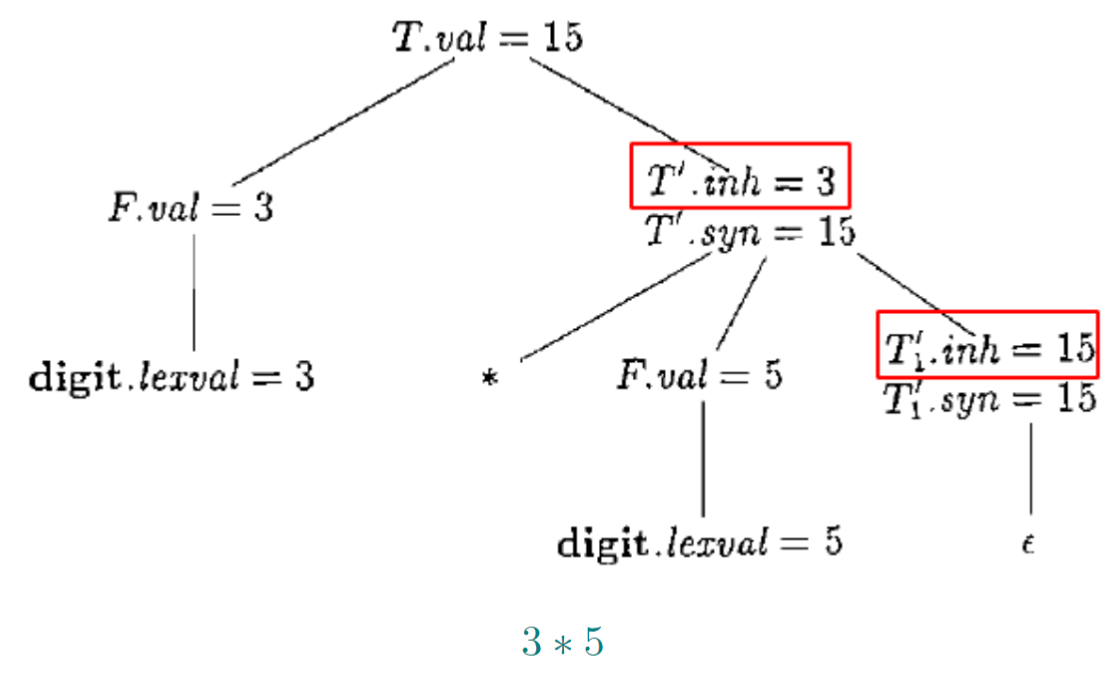
在右递归文法下实现了左结合

1.6.5. 依赖图用于确定一棵给定的语法分析树中各个属性实例之间的依赖关系

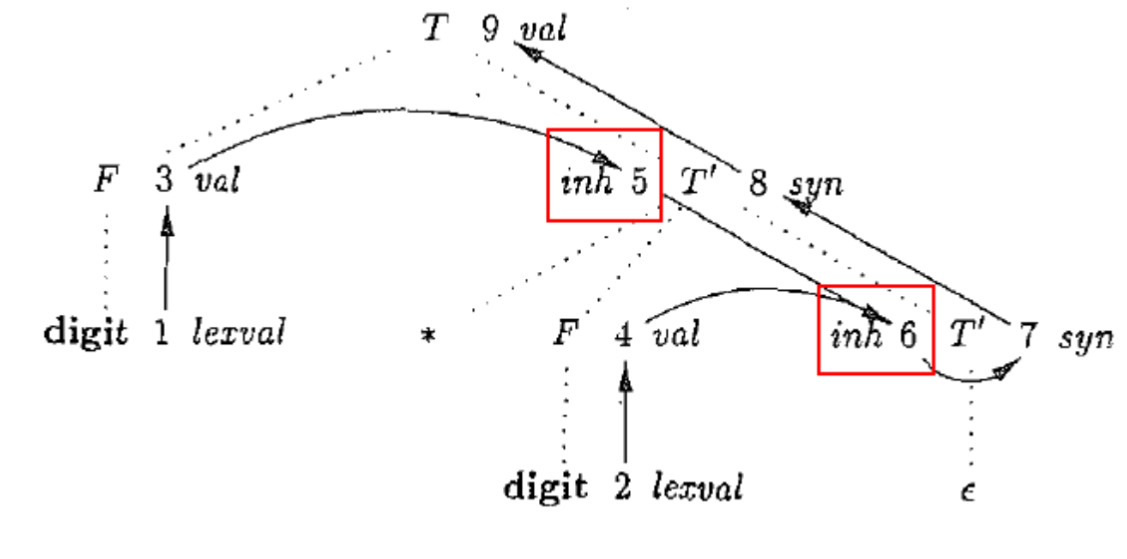
1. 信息流向:先从左向右、从上到下传递信息,再从下到上传递信息
2. 注意箭头的相关性
3. 为什么要传递：消除了左递归后的生成式所决定的
4. 右结合则不需要先计算：-、=、[]在c语言中是右结合运算符。

1.7. Definition (L属性定义(L-Attributed Definition))

1. 如果一个SDD的每个属性
   1. 要么是综合属性
   2. 要么是继承属性,但是它的规则满足如下限制:对于产生式$A \rightarrow X_1X_2...X_n$及其对应规则定义的继承属性$X_i.a$,则这个规则只能使用
      1. 和产生式头A关联的继承属性;
      2. 位于$X_i$左边的文法符号实例$X_1、X_2、...、X_{i−1}$相关的继承属性或综合属性;
      3. 和这个$X_i$的实例本身相关的继承属性或综合属性,但是在由这个$X_i$的全部属性组成的依赖图中不存在环。
2. 则它是L属性定义。
3. 只允许其依赖左侧的兄弟节点，避免出现环状结构。

1.8. 非L属性定义

$\begin{cases} 生成式 \\ A \Rightarrow B C \\ 语义规则 \\ A.s = B.b; \\ B.i = f(C.c, A.s) \\ \end{cases}$

作为继承属性,B.i依赖了右边的C.c属性与头部A.s综合属性
L属性文法:依赖图是无环的

• (左递归)S属性文法$\Rightarrow$(右递归)L属性文法

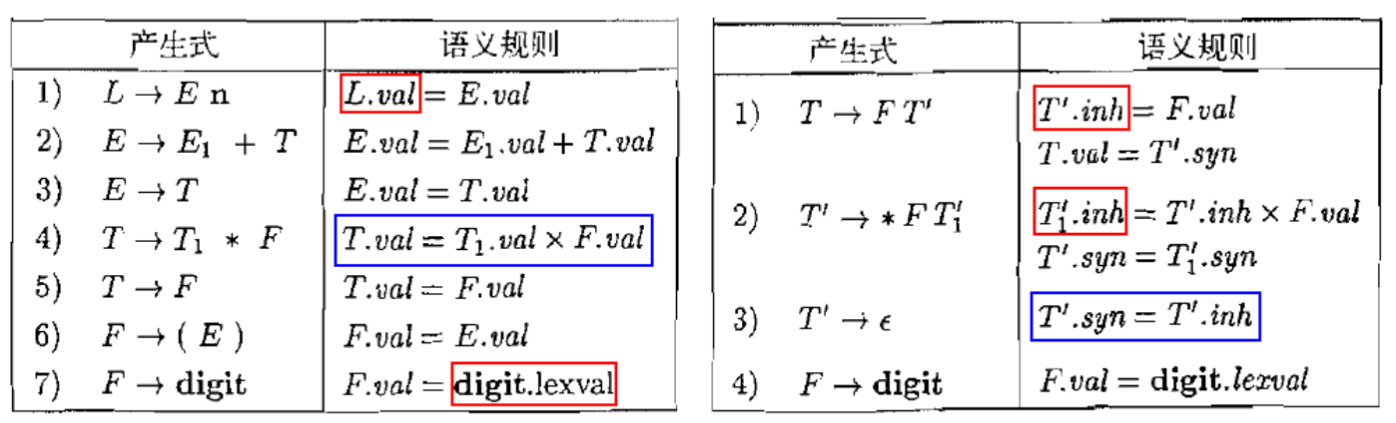
• 仍保持了操作的左结合性
• (左递归)S属性文法

$\begin{cases} A \rightarrow A_1Y & A.a = g(A_1.a, Y.y) \\ A \rightarrow X & A.a = f(X.x) \\ \end{cases}$

• (右递归)L属性文法

$\begin{cases} A \rightarrow XR & R.i = f(X.x); & A.a = R.s \\ R \rightarrow YR_1 & R_1.i = g(R.i, Y.y); & R.s = R_1.s \\ R \rightarrow \epsilon & R.s = R.i \\ \end{cases}$

1.9. 类型声明文法举例

1. 想要得到每一个变量的声明
2. L.inh将声明的类型沿着标识符列表向下传递,并被加入到相应的符号表条目

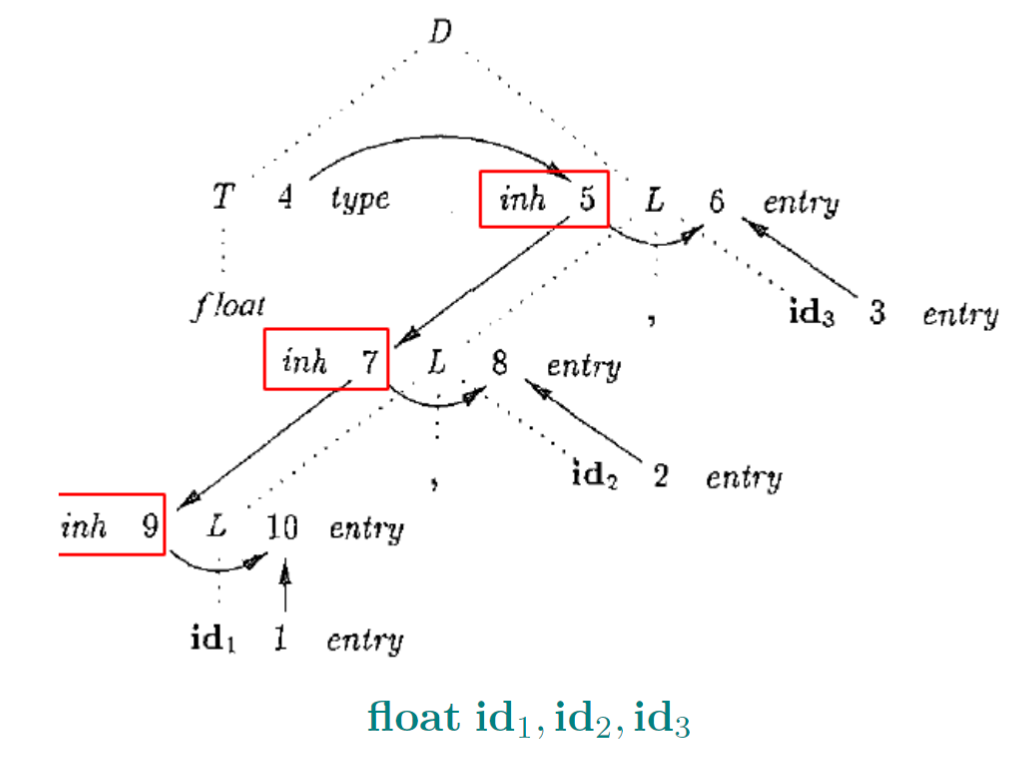
3. addType()是一种受控的副作用，可以理解为一种规则/动作，使用全局符号表，更易实现

1.10. 数组类型文法举例

1. 语义规则用以生成类型表达式array(2, array(3, integer))
2. 先检查继承属性，也就是基础信息
3. []是右结合的

1.10.1. 继承属性C.b将一个基本类型沿着树向下传播

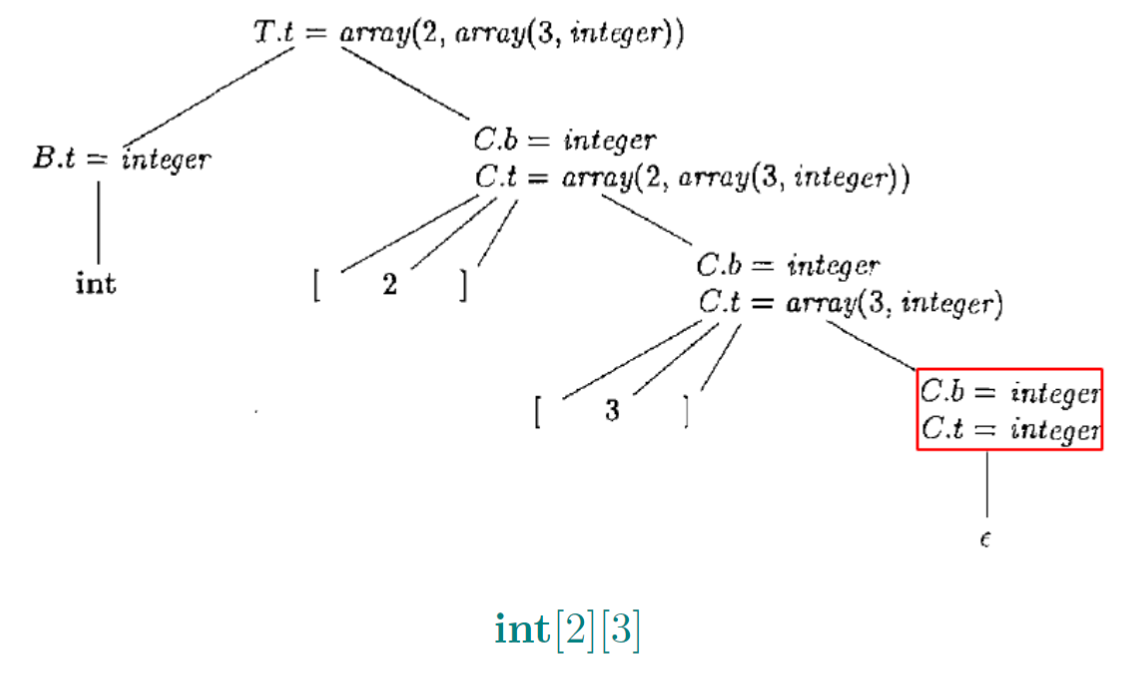
1. 综合属性C.t收集最终得到的类型表达式

1.11. 表达式的抽象语法树S属性定义

1. 没有消除左递归的表达式文法
2. 没有必要为()单独创造出节点

1.12. 抽象语法树:丢弃非本质的东西,仅保留重要结构信息

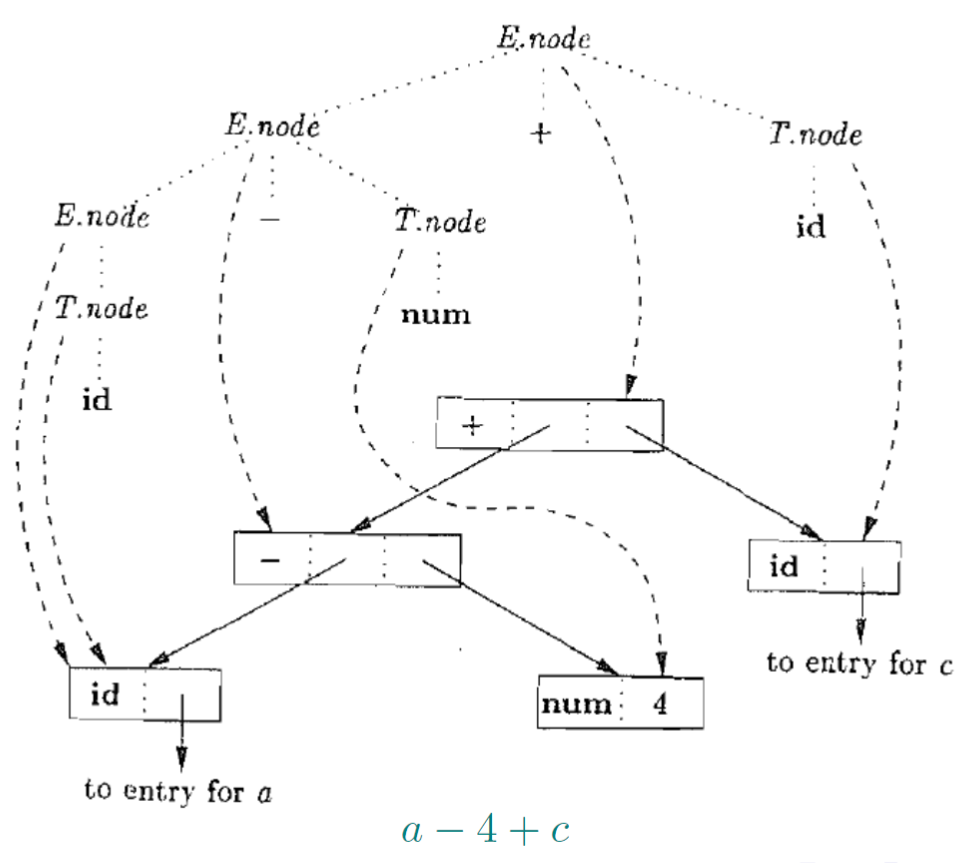
1. 点的部分显示出来的就是抽象语法树
2. 其实T.node和E.node都是使用一个节点来存储的
3. 其实本身()是在计算过程中除了优先级以外没有意义的
4. 抽象语法树比之前的语法树要简洁
5. 继承属性和综合属性之间如果没有其他节点，那么指向同一个节点

1.13. 表达式的抽象语法树L属性定义

1.14. Definition (后缀表示(Postfix Notation))

1. 如果E是一个变量或常量,则E的后缀表示是E本身;
2. 如果E是形如E1opE2的表达式,则E的后缀表示是E′1E′2op,这里E′1和E′2分别是E1与E2的后缀表达式;
3. 如果E是形如(E1)的表达式,则E的后缀表示是E1的后缀表示。

$(9−5)+2 \Rightarrow 95−2+ \\ 9−(5+2) \Rightarrow 952+− \\ 952+−3∗ \Rightarrow (9−(5+2))∗3 \\$

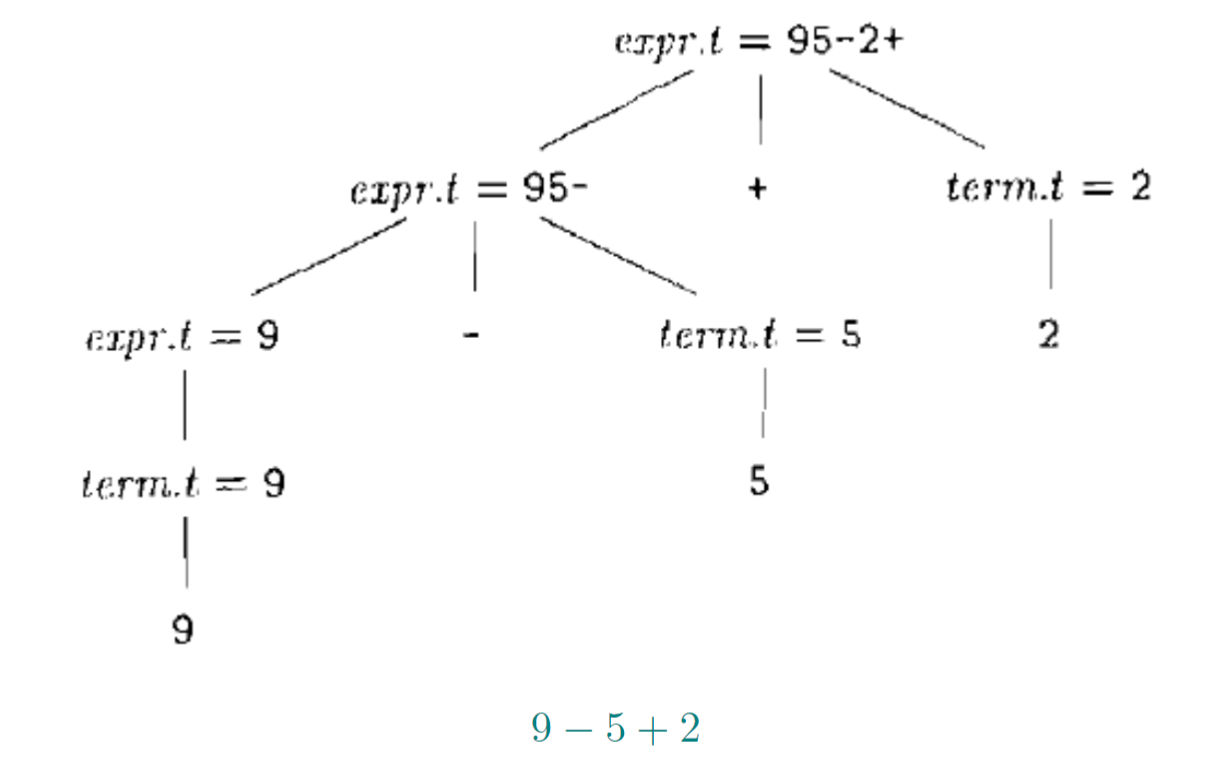
1.15. 后缀表达式S属性文法

"||"表示字符串的连接

1.16. 有符号二进制数文法

$-101_2 = -5_{10}$

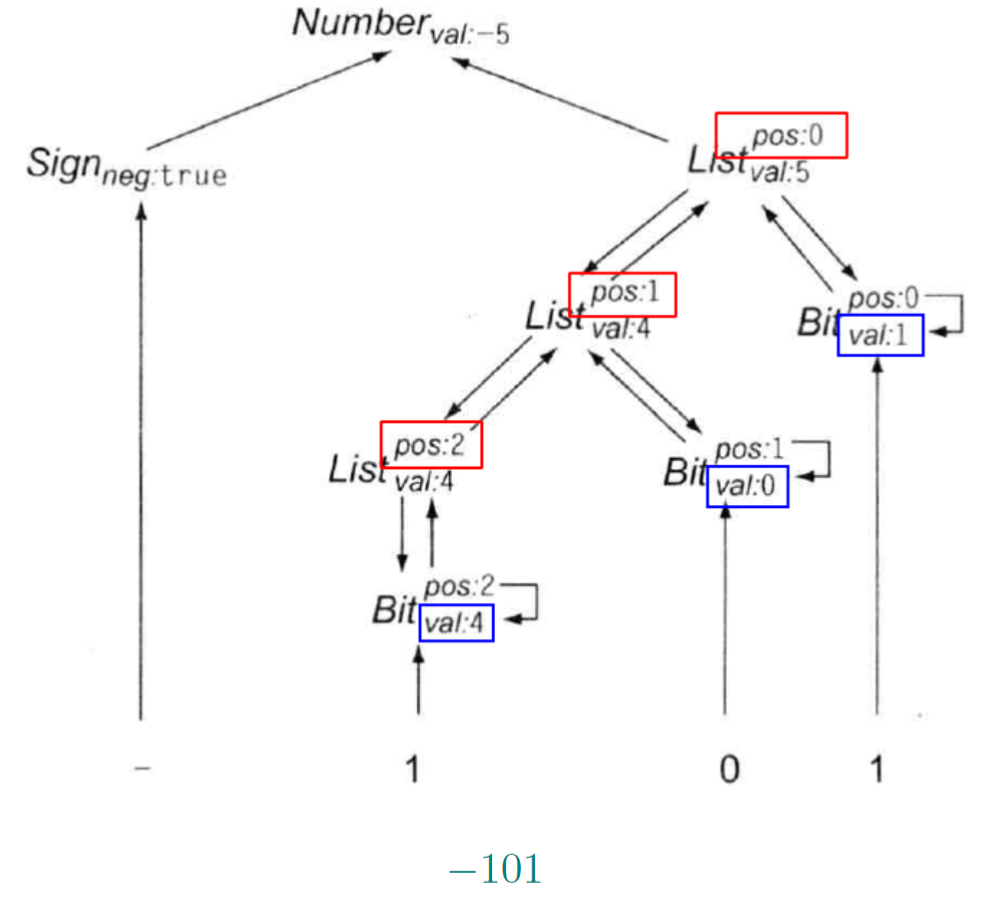
1.17. 有符号二进制数L属性定义

1. 是否可以去掉Bit.pos继承属性
2. 可以直接使用父节点list的pos值