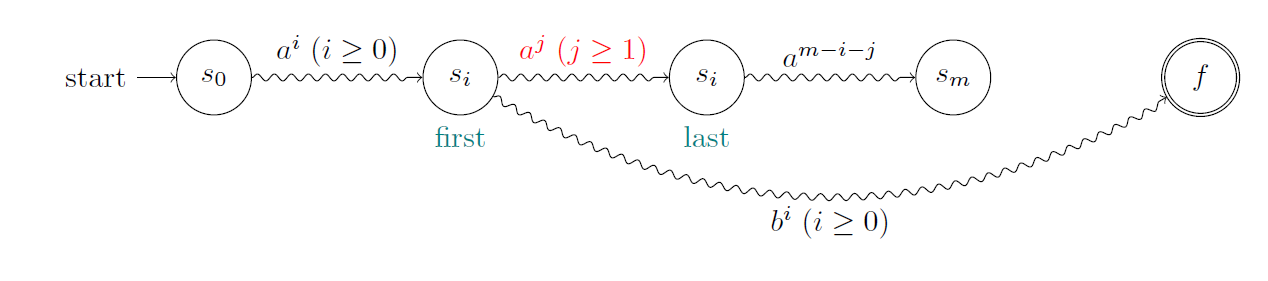上下文无关文法(CFG, Context-Free Grammer, 上下文无关文法)
- LL(1)可以完成手写分析器
- LR(1)可以更不容易出现细节问题
- Bison工具是本实验使用的工具。
1. 上下文无关文法(CFG)定义
- 上下文无关文法G是一个四元组G=(T,N,P,S):
- T是终结符号 Terminal集合, 对应于词法分析器产生的词法单元
- N是非终结符号 Non-terminal集合
- P是产生式 Production集合
A∈N→α∈(T∪N)∗
- 头部/左部(Head)A:
- 单个非终结符,必须只有一个,是命名为上下文无关文法的原因。
- 如果有多个则不符合上下文无关文法,会被成为上下文有关文法,但是几乎无法处理。
- 体部/右部(Body)α:
- 终结符与非终结符构成的串
- 也可以是空串ϵ
- S为开始(Start)符号
- 要求S∈N且唯一。
1.1. 上下文无关文法示例
- 一个符号要么是终结符号,要么是非终结符号
- 终结符号表示到此为止,无法再进行替换
G=({S},{(,)},P,S)S→SSS→(S)S→()
上面的文法表示任意嵌套的所有匹配好的括号串
G=({S},{a,b},P,S)S→aSbS→ϵ
可以有很多的情况
1.2. 条件语句文法
- 条件语句文法中包含悬空(Dangling)-else文法的问
- 这样的文法是有问题,我们进一步分析才可以,OTHER作为终结符。
1.3. 约定

约定: 如果没有明确指定, 第一个产生式的头部就是开始符号,用来避免写如上例子中的一些描述
1.4. 关于终结符号的约定
下述符号是终结符号:(通常的约定)
- 在字母表里排在前面的小写字母,比如a、b、c。
- 运算符号,比如+、*等。
- 标点符号,比如括号、逗号等。
- 数字,0、1、… 9。
- 黑体字符串,比如id或if。每个这样的字符串表示一个终结符号。
1.5. 关于非终结符号的约定
下述符号是非终结符号:
- 在字母表中排在前面的大写字母,比如A、B、C。
- 字母S。它出现时通常表示开始符号。
- 小写、斜体的名字,比如expr或stmt.
2. 语义
- 上下文无关文法G定义了一个语言L(G)
- 语言是串的集合
3. 推导(Derivation)的定义
3.1. 表达式文法
E→−E∣E+E∣E∗E∣(E)∣id
- 推导即是将某个产生式的左边替换成它的右边
- 每一步推导需要选择替换哪个非终结符号,以及使用哪个产生式
E⇒−E⇒−(E)⇒−(E+E)⇒−(id+E)⇒−(id+id)
E⇒−E:经过一步推导得出E+−(id+E):经过一步或多步推导得出E∗−(id+E):经过零步或多步推导得出
E⇒−E⇒−(E)⇒−(E+E)⇒−(E+id)⇒−(id+id)
如果S∗α,且α∈(T∪N)∗,则称α是文法G的一个句型(包含非终结符)
E→−E∣E+E∣E∗E∣(E)∣idE⇒−E⇒−(E)⇒−(E+E)⇒−(id+E)⇒−(id+id)
3.3. Definition (Sentence,句子)
- 如果S∗w,且w∈T∗,则称w是文法G的一个句子(没有非终结符了)
- 句子就是这个语言中的串
4. Definition (文法G生成的语言L(G))
文法F的语言L(G)是它能推导出的所有句子构成的集合。
w∈L(G)⇔S∗w
4.1. 关于文法G的两个基本问题
- Membership问题:给定字符串x∈T∗,x∈L(G)?字符串可不可以由文法推理得到
- L(G)究竟是什么?
4.1.1. 问题一:Membership问题
- 给定字符串x∈T∗,x∈L(G),(即检查x是否符合文法G)
- 这就是语法分析器的任务:为输入的词法单元流寻找推导、构建语法分析树, 或者报错
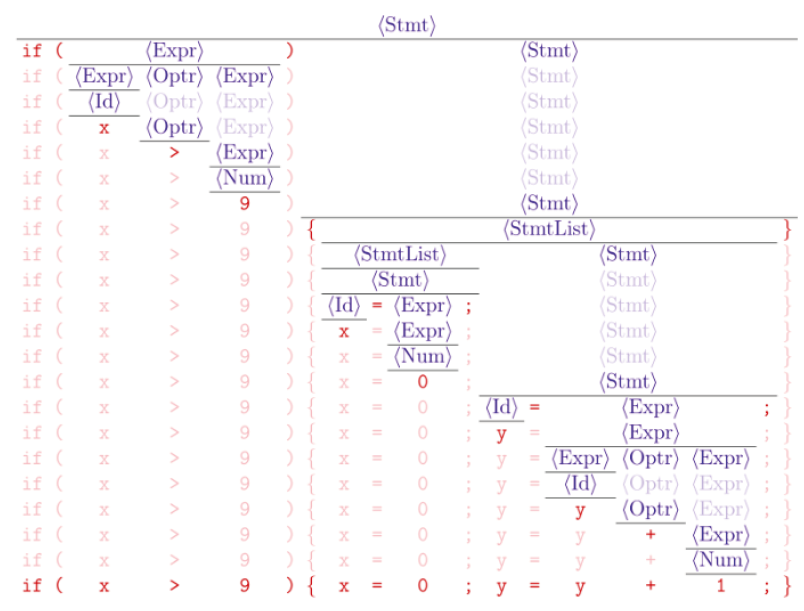
- 根节点是文法G的起始符号
- 叶子节点是输入的词法单元流
- 常用的语法分析器以自顶向下或自底向上的方式构建中间部分
4.1.2. 问题二:L(G) 是什么?
这是程序设计语言设计者需要考虑的问题
4.1.2.1. 根据文法G推导语言L(G)
例子一
S→SSS→(S)S→()S→ϵL(G)={良匹配括号串}
例子二
S→aSbS→ϵL(G)=anbn∣n≥0
4.1.2.2. 根据语言L(G)来推导文法G
- 目标生成:字母表∑=a,b上的所有回文串(Palindrome)构成的语言
S→aSaS→bSbS→aS→bS→ϵS→aSa∣bSb∣a∣b∣ϵ
- 目标生成:bnamb2n∣n≥0,m≥0
S→bSbb∣AA→aA∣ϵ
- 目标生成:{x∈{a,b}∗∣x中a,b个数相同}
- 证明:a可以是空串
- 证明:a以a开头,那么后面肯定能找到一个b保证被分为了aVbV并且V中的ab数量均相同,以b开头类似。
V→aVbV∣bVaV∣ϵ
- 目标生成:{x∈{a,b}∗∣x中a,b个数不同}
- T表示a多一个或者更多
- U表示b多一个或者更多
- UT不能同时出现,和V去组合即可
- 证明
S→T∣UT→VaT∣VaVU→VbU∣VbVV→aVbV∣bVaV∣ϵ
4.2. 顺序语句、条件语句、打印语句

上图中的L是顺序语句
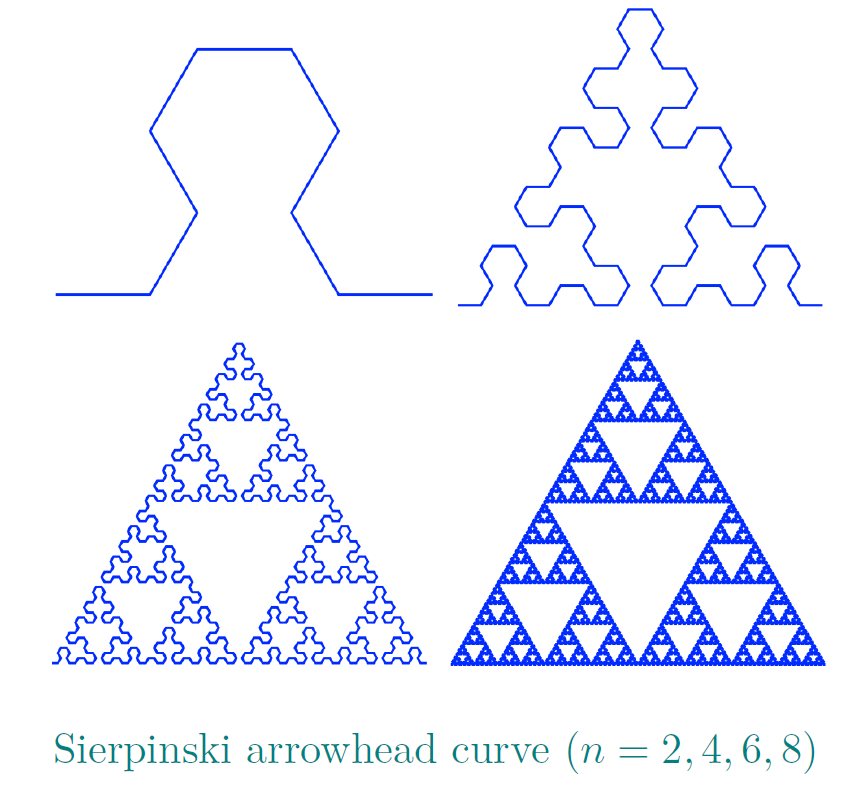
5. L-System(不考)
L-System:这不是上下文无关文法, 但精神高度一致
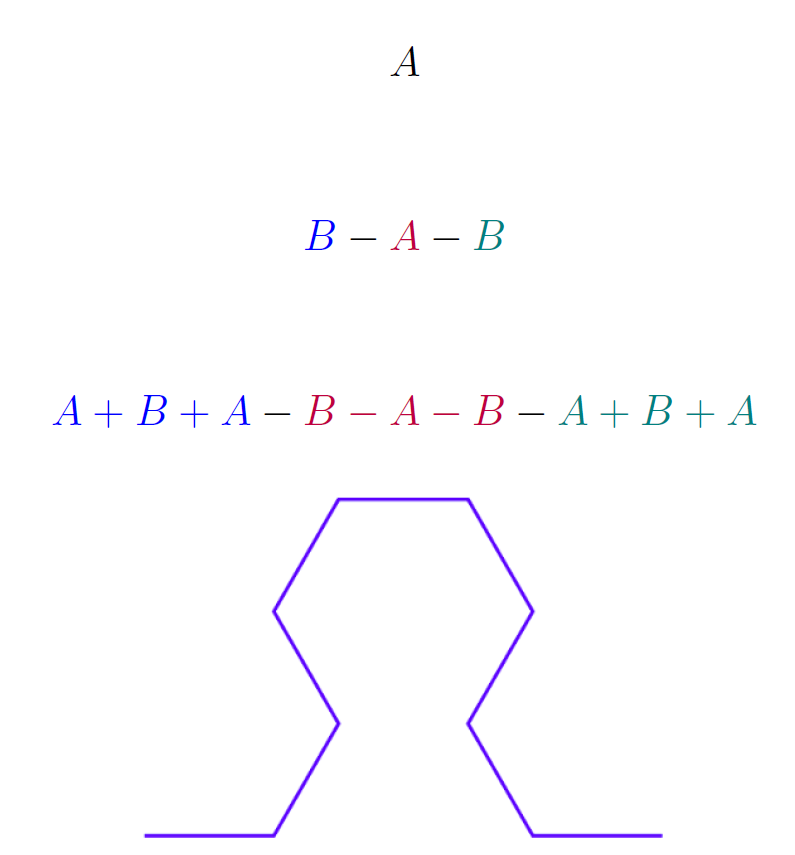
variables:ABconstants:+−start:Arules:(A→B−A−B),(B→A+B+A)angles:60′
- A,B:向前移动并画线
- +:左转
- -:右转
- 每一步都并行地应用所有规则
variables:XYconstants:F+−start:FXrules:(X→X+YF+),(Y→−FX−Y)angles:90′
- F:向前移动并画线
- +:右转
- -:左转
- X:仅用于展开,在作画时被忽略
- 每一步都并行地应用所有规则
6. 最左(leftmost) 推导与最右(rightmost) 推导
E→E+E∣E∗E∣(E)∣idElm−Elm−(E)lm−(E+E)lm−(id+E)lm−(id+id)
- Elm−E:经过一步最左推导得出
- E+lm−(id+E):经过一步或多步最左推导得出
- E∗lm−(id+E):经过零步或多步最左推导得出
- 最左推导是有非终结符优先选择最左侧的进行推导
- 最右推导是有非终结符有限选择最右侧的进行推导
Erm−Erm−(E)rm−(E+E)rm−(E+id)rm−(id+id)
- 如果S∗lmα, 并且α∈(T∪N)∗,则称α是文法G的一个最左句型。
Elm−Elm−(E)lm−(E+E)lm−(id+E)lm−(id+id)
- 如果S∗rmα, 并且α∈(T∪N)∗,则称α是文法G的一个最右句型。
Erm−Erm−(E)rm−(E+E)rm−(id+E)rm−(id+id)
7. 语法分析树
- 语法分析树是静态的, 它不关心动态的推导顺序
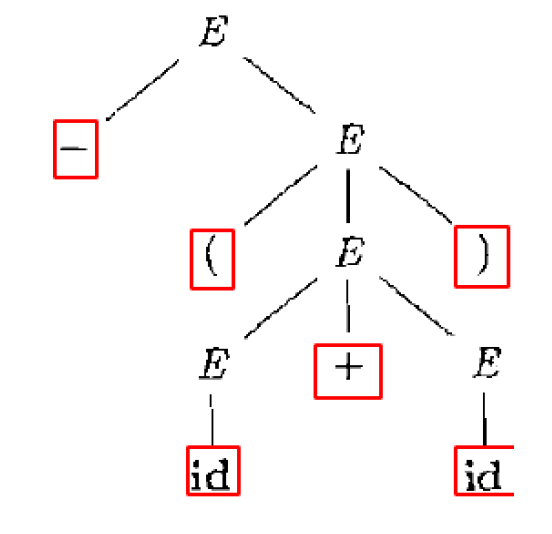
- 一棵语法分析树对应多个推导
- 但是, 一棵语法分析树与最左(最右) 推导一一对应
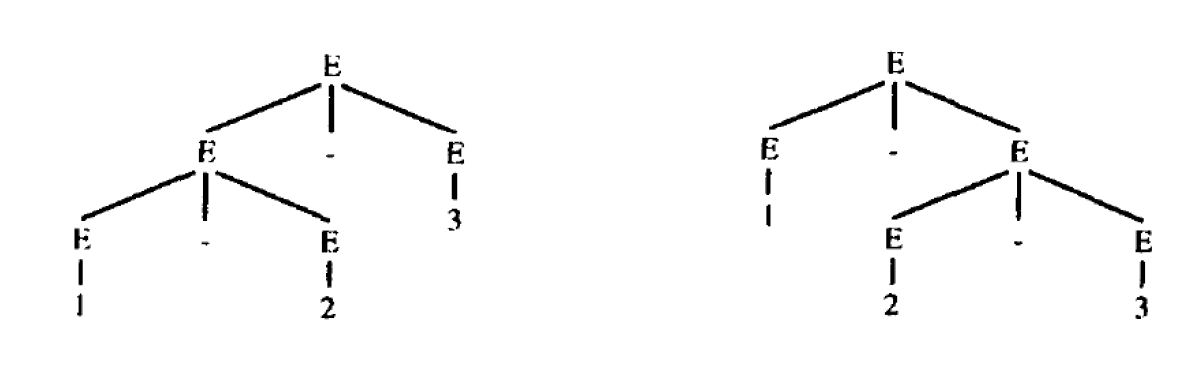
7.1. 二义性引入
- 1 - 2 - 3的语法树的两种不同表达形式
- 以下的两棵语法树是不同的,生成出来的目标代码也是不同的
- 这个文法是有问题的,这个文法具有二义性,我们需要通过修改文法避开二义性问题。
- 语法没有二义性的描述,L(G)本身只是一个串的集合。
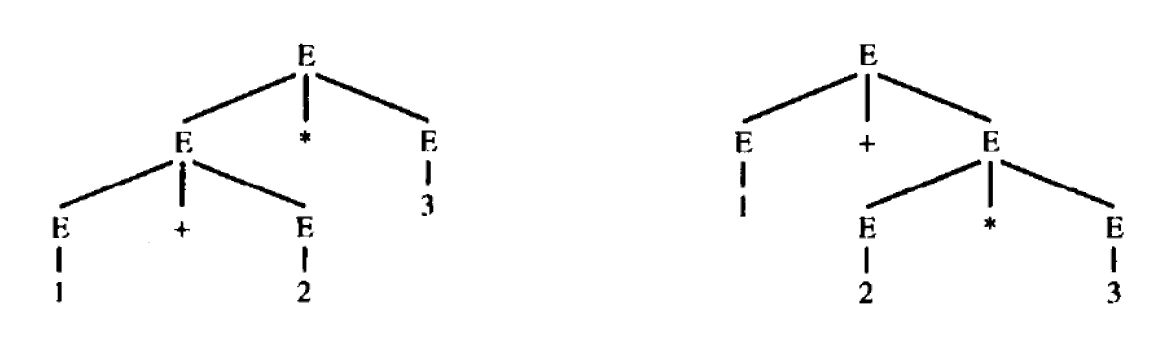
7.2. Definition (二义性(Ambiguous) 文法)
- 如果L(G) 中的某个句子有一个以上语法树/最左推导/最右推导,则文法G是二义性的。
- 1 + 2 * 3的语法树
7.3. 悬空-else
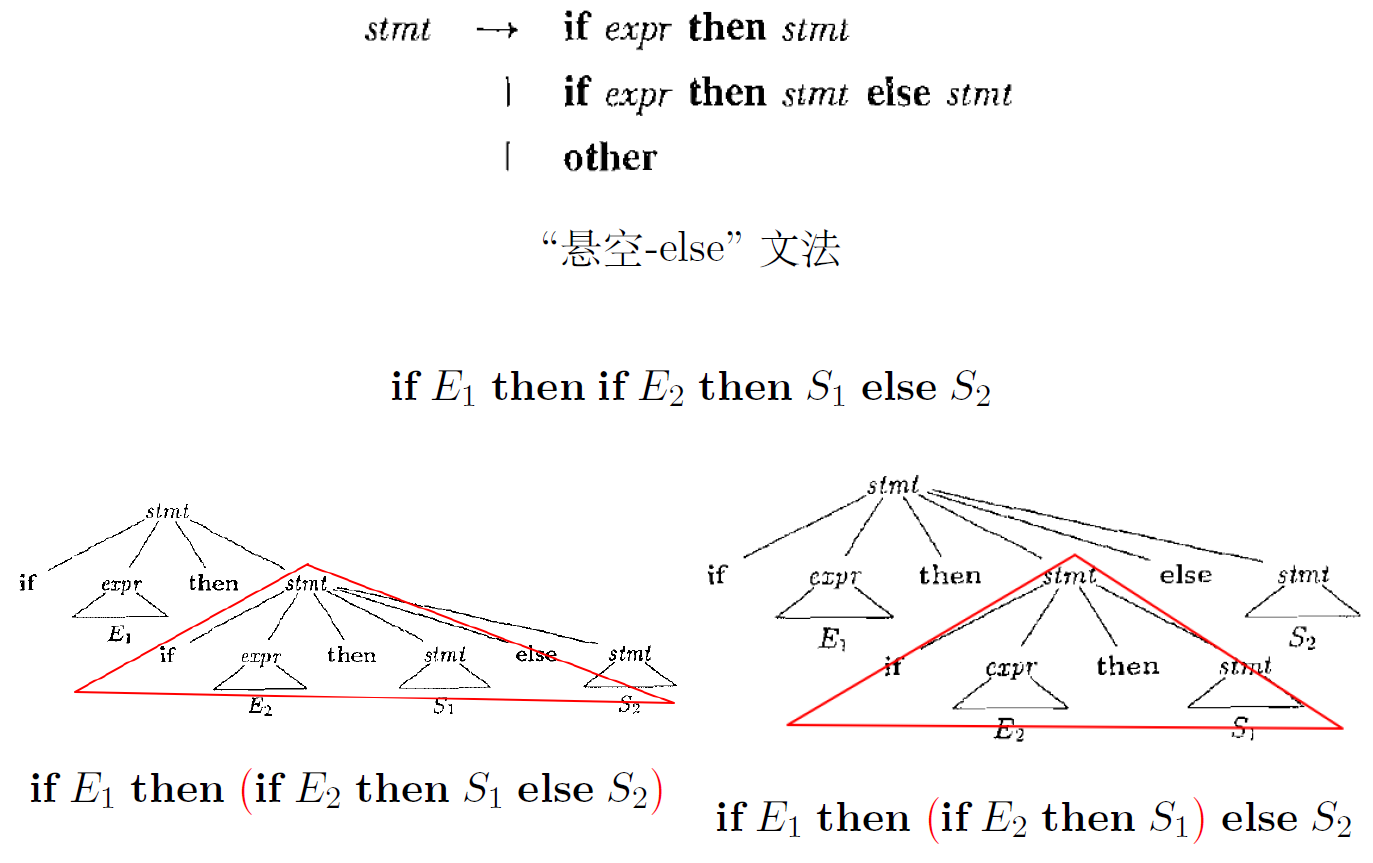
8. 二义性文法
- 不同的语法分析树产生不同的语义
- 所有语法分析器都要求文法是无二义性的
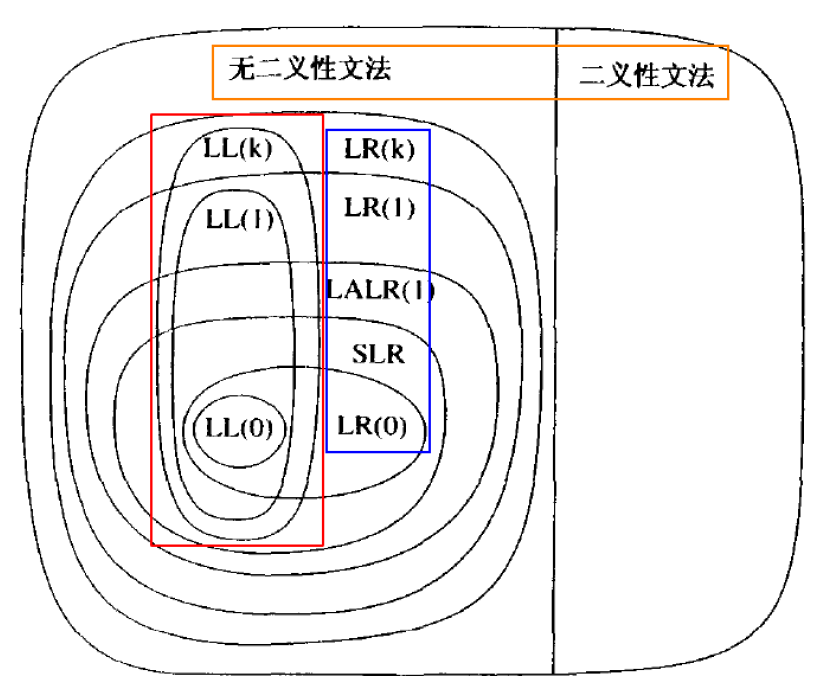
- Q:如何识别二义性文法?这是不可判定的问题,是指没有通用的算法,可以判断任意的文法G
- Q:如何消除文法的二义性?
8.1. 消除文法二义性
- 四则运算均是左结合的
- 优先级: 括号最先, 先乘除后加减
- 二义性表达式文法以相同的方式处理所有的算术运算符
- 要消除二义性, 需要区别对待不同的运算符
- 将运算的"先后" 顺序信息编码到语法树的"层次"结构中
E→E+E∣id
8.2. 左结合文法
E→E+TT→id
8.3. 右结合文法
E→T+ET→id
8.4. 使用左(右)递归实现左(右)结合
8.5. 括号最先, 先乘后加文法
乘号更靠近叶子节点
E→E+E∣E∗E∣(E)∣idE→E+T∣TT→T∗F∣FF→(E)∣id
8.6. Summary
E→E+E∣E−E∣E∗E∣E/E∣(E)∣id∣numberE→E+T∣E−T∣TT→T∗F∣T/F∣FF→(E)∣id∣number
- 无二义性的表达式文法
- E:表达式(expression)
- T:项(term)
- F:因子(factor)
- 将运算的"先后"顺序信息编码到语法树的"层次"结构中
8.7. IF-Then-Else问题
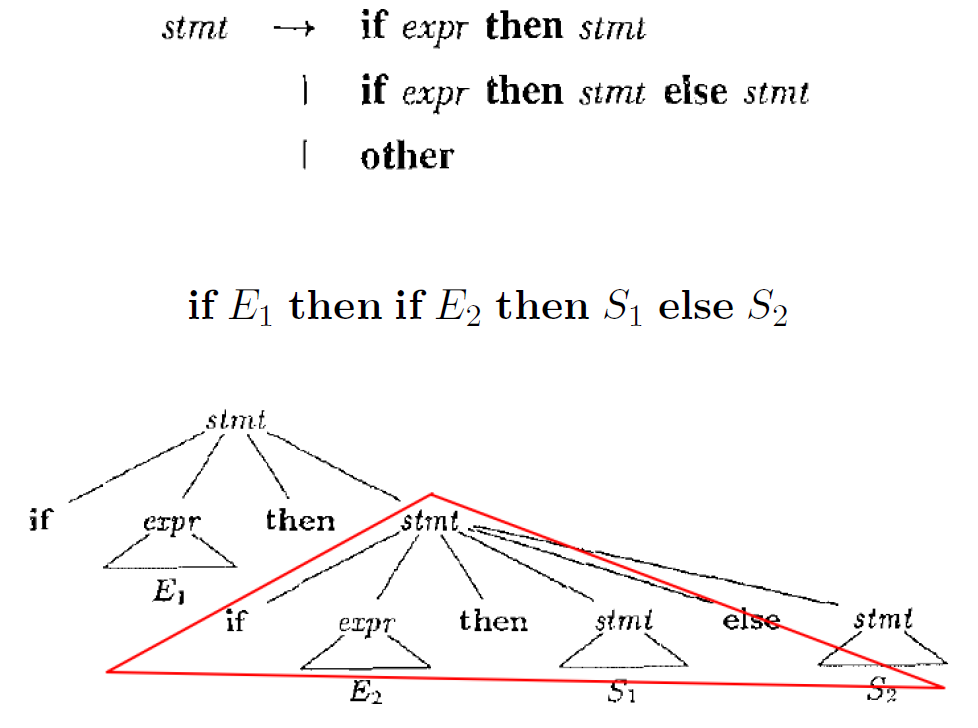
每个else与最近的尚未匹配的then匹配

- 基本思想: then与else之间的语句必须是"已匹配的"
- 证明两件事情:证明部分不作为重点
- L(G)=L(G′)
- G′是无二义性的
8.7.1. L(G)=L(G′)证明过程

L(G′)⊆L(G)简单容易证明
文法是递归的,我们可以使用数学归纳法,对推导步骤进行归纳
L(G)⊆L(G′)x∈L(G)→x∈L(G′)stmt→...→x
- 只要G中展开一步,G’中都有相应的对应即证明了L(G)⊆L(G′)
8.7.2. G′ 是无二义性的
- 每个句子对应的语法分析树是唯一的
- 只需证明: 每个非终结符的展开方式是唯一的
L(matched_stmt)∩L(open_stmt)=∅L(matched_stmt1)∩L(matched_stmt2)=∅L(open_stmt1)∩L(open_stmt2)=∅
上面的下标代表子句
- Q:为什么不使用优雅、强大的正则表达式描述程序设计语言的语法?
- A:正则表达式的表达能力严格弱于上下文无关文法
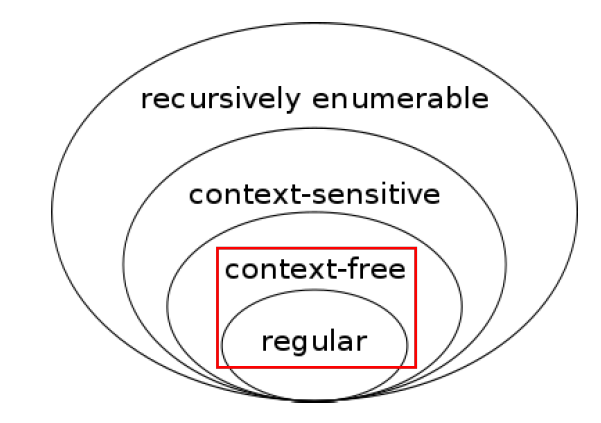
每个正则表达式r对应的语言L® 都可以使用上下文无关文法来描述
r=(a∣b)∗abb
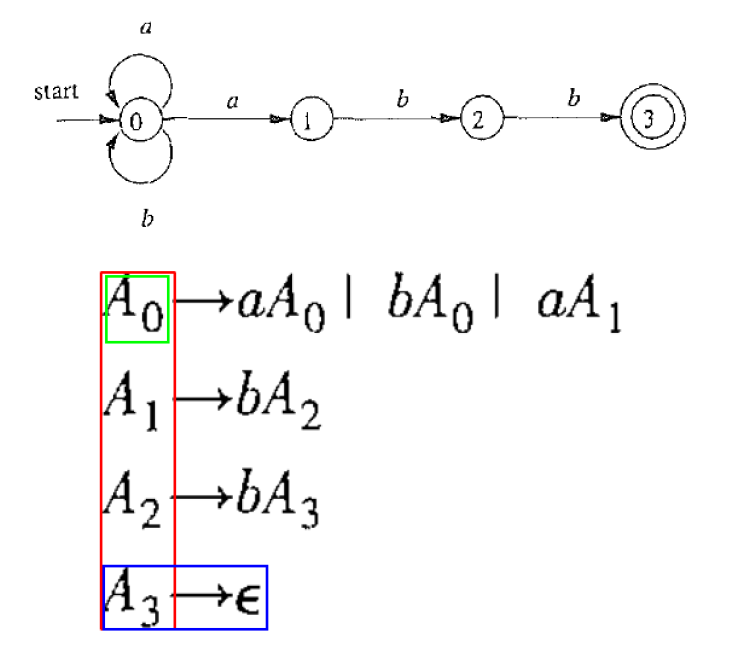
- 此外, 若δ(Ai,ϵ)=Aj,则添加Ai→Aj
S→aSbS→ϵL=anbn∣n≥0
- 该语言无法使用正则表达式来描述
- 定理:L={anbn∣n≥0} 无法使用正则表达式描述
- 反证法
- 假设存在正则表达式r:L(r)=L
- 则存在有限状态自动机D®:L(D(r))=L; 设其状态数为k
- 考虑输入am(m>k)
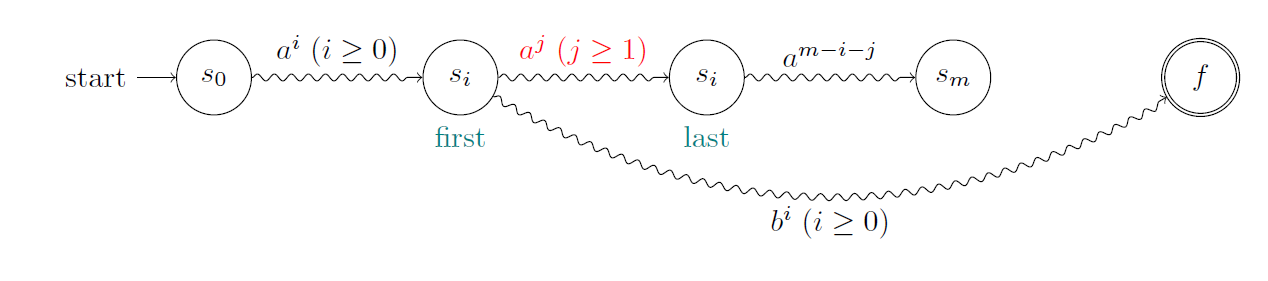
- D(r)也能接受a{i+j}bi,矛盾!
- Pumping Lemma for Regular Languages:L=anbn∣n≥0
- Pumping Lemma for Context-free Languages:L=anbncn∣n≥0
- 只考虑无二义性的文法这意味着,每个句子对应唯一的一棵语法分析树