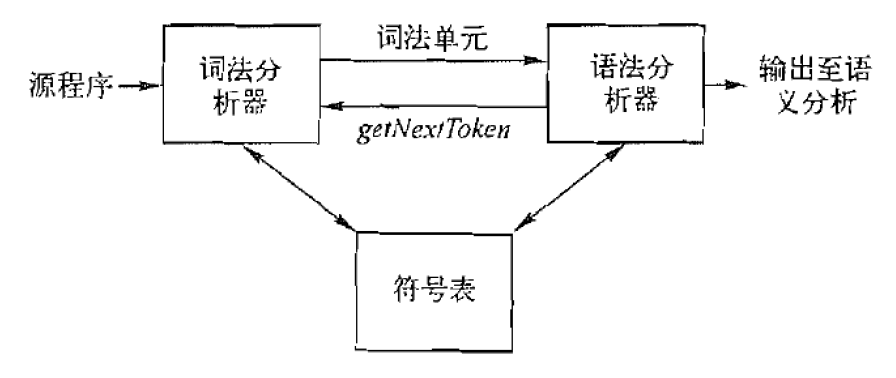
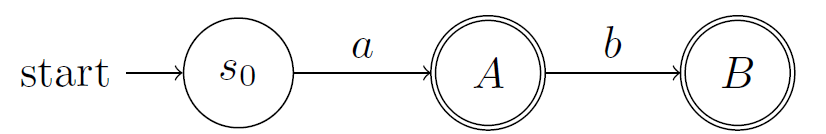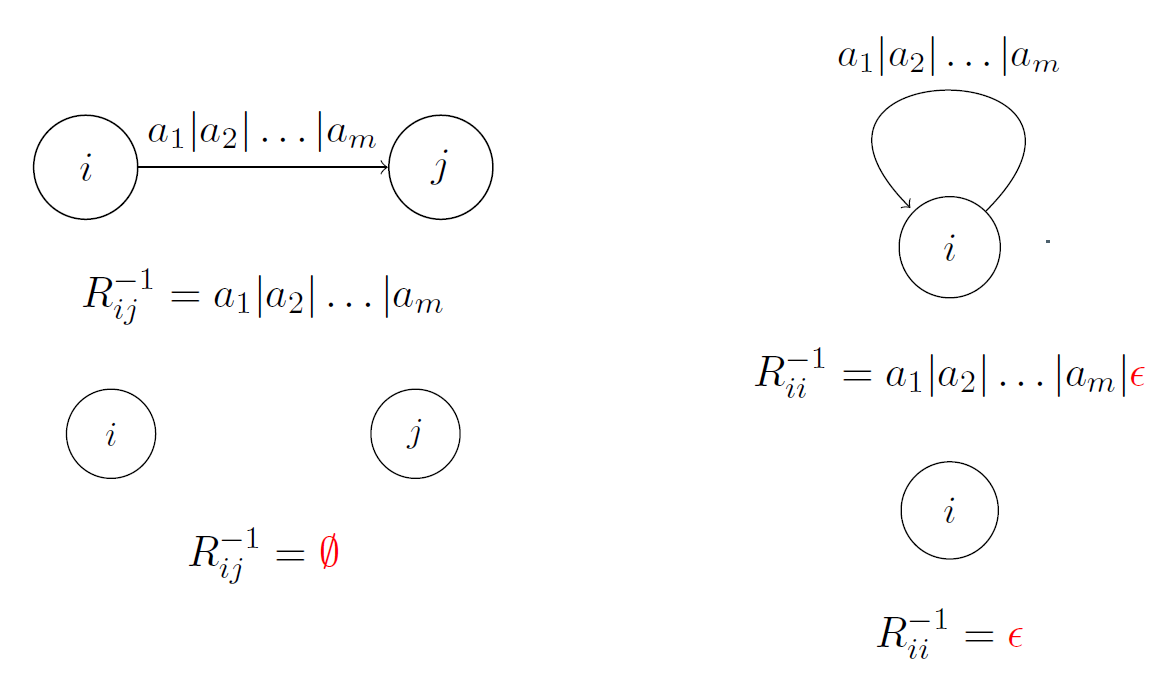词法分析
输入:程序文本/字符串s和词法单元(token)的规约
输出:词法单元流
token: <token-class, attribute-value>
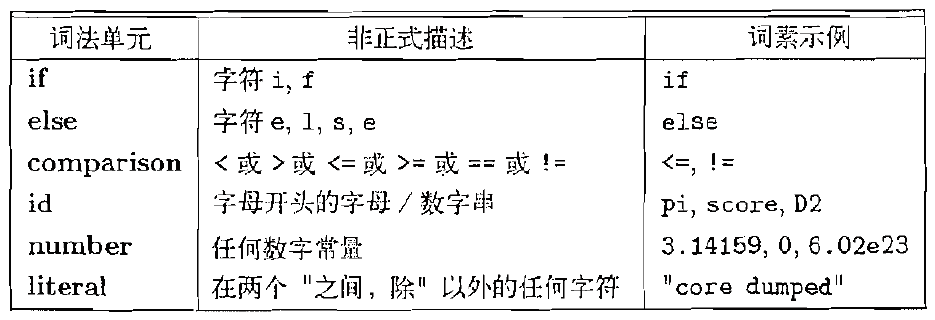
词法单元
非正式描述
词素示例
if
字符i、f
if
else
字符e、l、s、e
else
comparision
< 或 > 或 <= 或 >= 或 == 或 !=
<= , !=
id
字符开头的字母/字符串
pi, score, D2
number
任何字符常量
3.14
literal
在两个"之间,处理"以外的任何字符
“core dumped”
int/if:关键词
ws:空格、制表符、换行符
comment:"//" 开头的一行注释或者"/* */" 包围的多行注释
1 2 3 int main (void ) printf ("hello, world\n" )
词法分析的结果:本质上,就是一个**字符串(匹配/识别)**算法
1 2 3 4 int ws main/id LP void RP ws ws ws id LP literal RP SC ws
生产环境下的编译器(如gcc) 通常选择手写词法分析器
手写词法分析器
词法分析器的生成器
自动化词法分析器
flex是自动的词法分析器
词法分析器相对比较简单,手写词法分析器可以做一些人为的优化。
gcc中,c语言的lex是1400多行,而c++的lex则是4000多行代码,number是最复杂的,包含不同进制、字母等问题,课程与gcc有一定差异
识别字符串s中符合某种词法单元模式 的所有词素
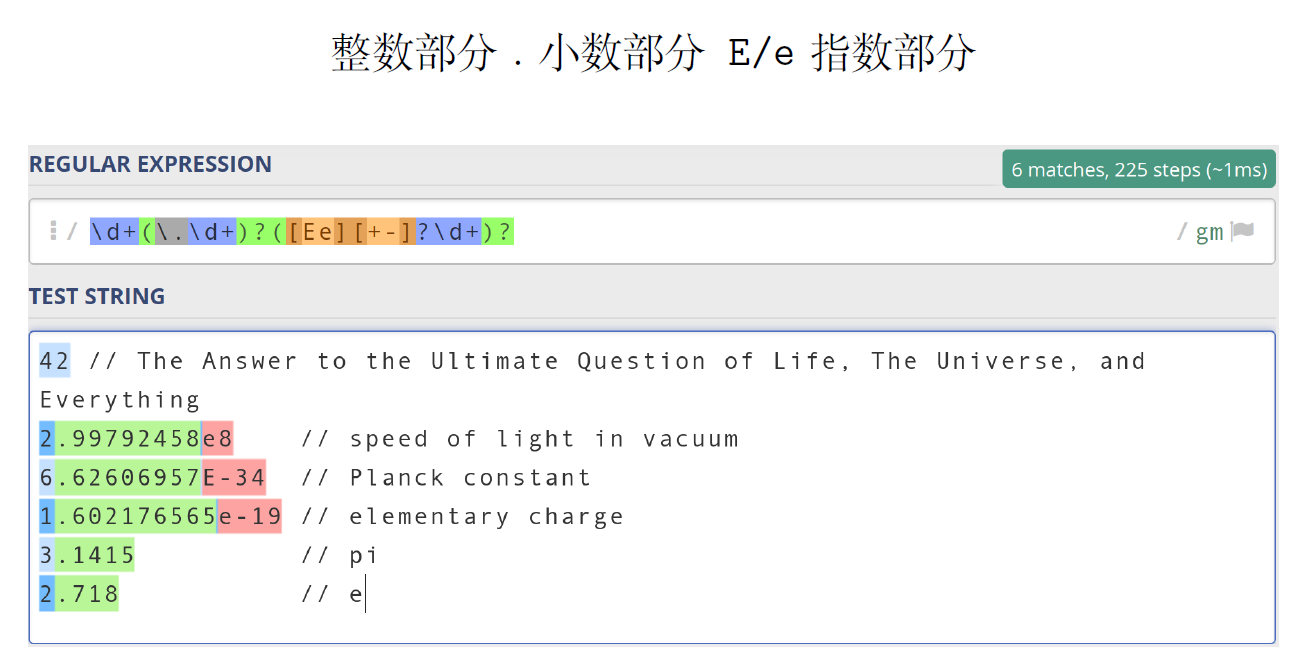
1 2 3 4 5 if ab42 >= 3.14 :2.99792458E8 else 2.718 1024
这里的分割不适宜使用空格,例如ab42>=42则空格分割不出来。
1 2 3 4 ws if else id integerrelop (关系运算符) sci (识别实数,带科学技术发和不带的)assign (:=)
识别字符串s中词素某种词法单元模式 的前缀词素
识别字符串s中符合特定词法单元模式 的前缀词素 (例如识别符合id的模式的开头的第一个词素)
注意:这里的第一个词素就只看第一个,而不是找到符合要求的第一个
最重要的是状态转移图
识别字符串s中符合特定词法单元模式的前缀词素
分支:先判断属于哪一类, 然后进入特定词法单元的前缀词素匹配流程
识别字符串s中符合某种词法单元模式的前缀词素
循环:返回当前识别出来的词法单元与词素, 继续识别下一个前缀词素
识别字符串s中符合某种词法单元模式的所有词素
1 2 3 4 先: ws if else id integer real sci
特定词法单元模式 的开头第一个词素 1 2 3 public int line = 1 ;private char peek = " " ;private Hashable words = new Hashtable ();
line:行号, 用于调试
peek:下一个向前看字符(Lookahead)
words:从词素到词法单元标识符或关键词的映射表
1 2 3 // 先将关键字方进去words .put ("if" , if )words .put ("else" , else )
1 2 3 4 5 6 7 8 public Token scan () throws IOException{for (;;peek=(char )System.in.read()){if (peek == " " || peek == "\t" ) continue ;else if (peek == "\n" ) line = line + 1 ;else break ;
1 2 3 4 5 6 peek = next input char acter ;while ( peek != null ) {char acter
char peek = " ":下一个向前看字符
例子:123abc,得到<number, 123>和<id, abc>
注意上文中123读取完了之后跳出的是a位置,不能入上面第二个部分,不然会丢东西。
上图数字没有含义
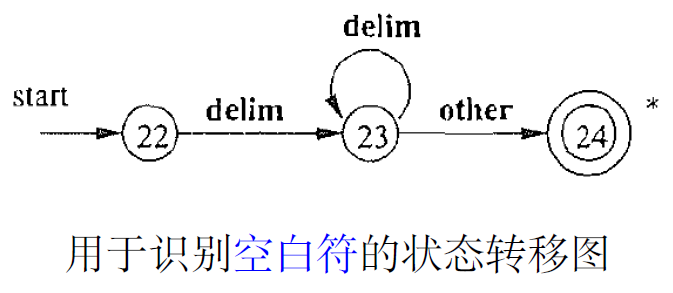
重要是,当前识别的出的空白符不包含 当前peek指向的字符
22:碰到other怎么办?
上图中的*表示,必须是当前的词开始。
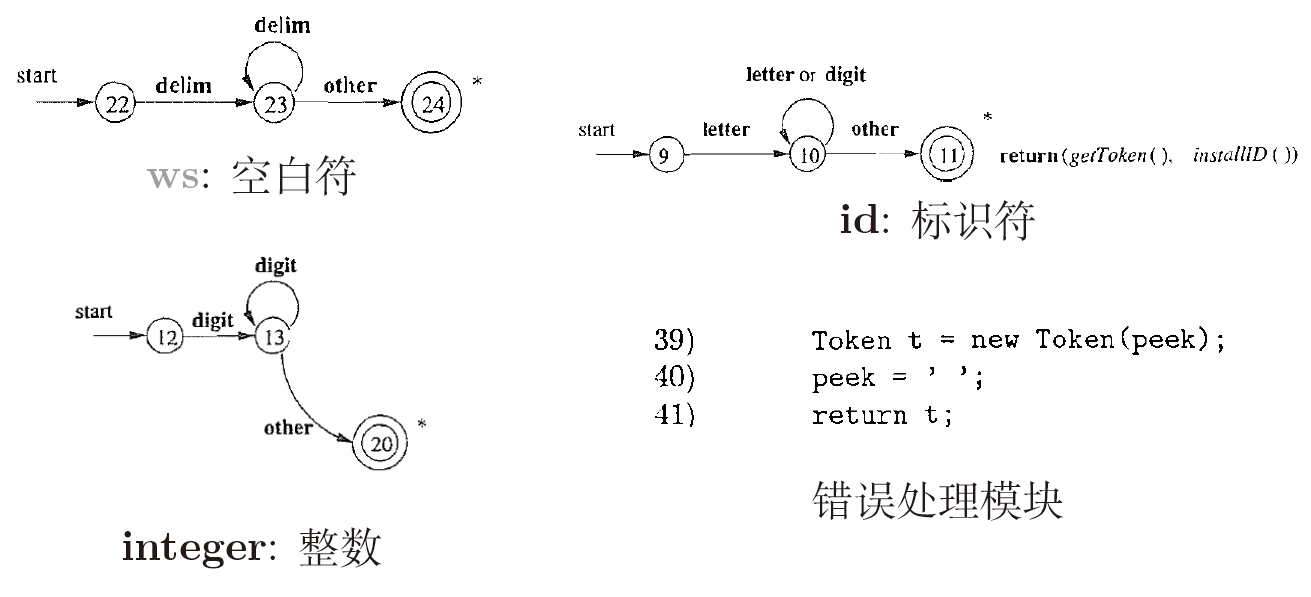
integer : 整数(允许以0开头)1 2 3 4 5 6 7 8 if ( Character.isDigit(peek) ) {int V = 0 ;do {10 * v + Character.digit(peek, 10 );char )System.in.read();while (Character.isDigit(peek));return new Num (v);
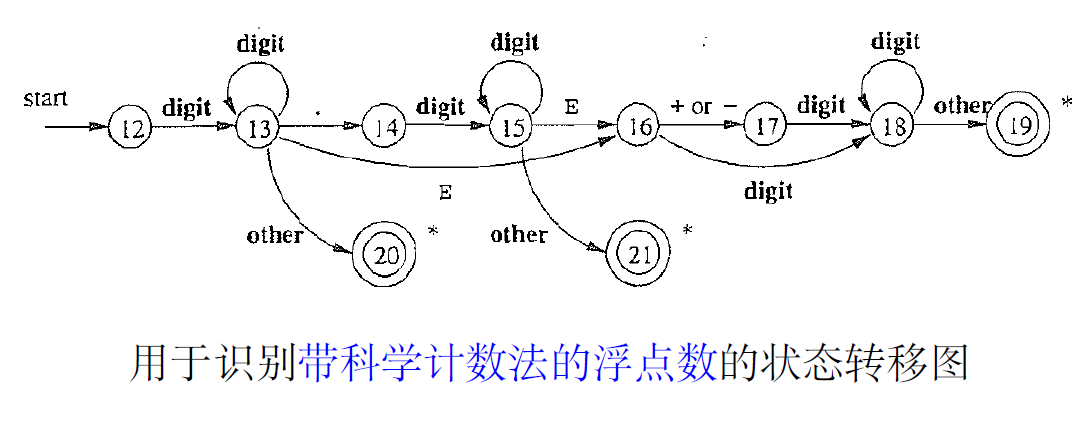
12:碰到other如何处理?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 if (Character.isLetter(peek) ) {StringBuffer b = new StringBuffer () ;do {char )System.in.read();while (Character.isLetter0rDigit(peek));String s = b.toString();Word W = (Word)words.get(s);|if (w != null ) return w;new Word (Tag.ID, s) ;return w;
识别词素、判断是否是预留的关键字或已识别的标识符 、保存该标识符
9:碰到other怎么处理?
1 2 3 Token t = new Token (peek);" " ;return t;
错误处理模块:出现词法错误 , 直接报告异常字符
关键点 :合并22, 12, 9, 根据下一个字符 即可判定词法单元的类型否则, 调用错误处理模块(对应other), 报告该字符有误 , 并忽略该字符
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 package lexer; import java.io.*;import java.util.*;public class Lexer {public lnt llne = 1 ;private char peek = " " ;private Hashtable words = new Hashtable ();void reserve (Word t) { words.put(t.lexeme, t);}public Lexer () {new Word (Tag.TRUE, "true" ));new Word (Tag.FALSE, "false" ));public Token scan () throws I0Exception {for (;; peek = (char )System.in.read()) {if ( peek == " " | | peek == '\t' ) continue ;else if ( peek == '\n' ) line = line + 1 ;else break ;if (Character.isDigit(peek)){int v=0 ;do {10 * v + Character.digit(peek, 10 ) ;char )System.in.read();while (Character.isDigit(peek));return new Num (v);if (Char acter.isLetter(peek)) {StringBuffer b = new StringBuffer ();do {char )System.in.read() ;while (Character.isLetter0rDigit(peek));String s = b.toString();Word w = (Word)words.get(s);if ( w != null ) return w;new Word (Tag.ID, s);return w;new Token (peek) ;" " ;return t;
外层循环 调用scan() (不考虑语法分析)
或者由语法分析器按需 调用scan() ,语法分析器每次从词法分析器中提取到下一个token,检查是不是自己想要的下一个词。
回溯之前的问题
relop: < > <= >= == <>
最长优先原则: 例如, 识别出<=, 而不是< 与=
注意:此处的=是判断是否相等的关系运算符。如果=表示赋值,而==表示判断,如何设置词法分析器
问题:0的时候遇到other如何处理?
关键点: 合并22, 12, 9, 0, 根据下一个字符 即可判定词法单元的类型
否则, 调用错误处理模块(对应other), 报告该字符有误 , 并忽略该字符
我们可以类似关系运算符来识别各种数字吗?比如将real、sci分开识别,然后合并会有什么问题?
ws if else id integer relop前一个词法分析器的前提如下(而现在并不满足这样子)
根据下一个字符 即可判定词法单元的类型
每个状态转移图的每个状态要么是接受状态 , 要么带有other 边
问题:如何同时识别real和sci
上图中主要展示了正确的流程
我们可以认识到,看任意个字符我们都无法确定到底进入哪一个,这也就解释了为什么我们不可以类似关系运算符来确定状态。
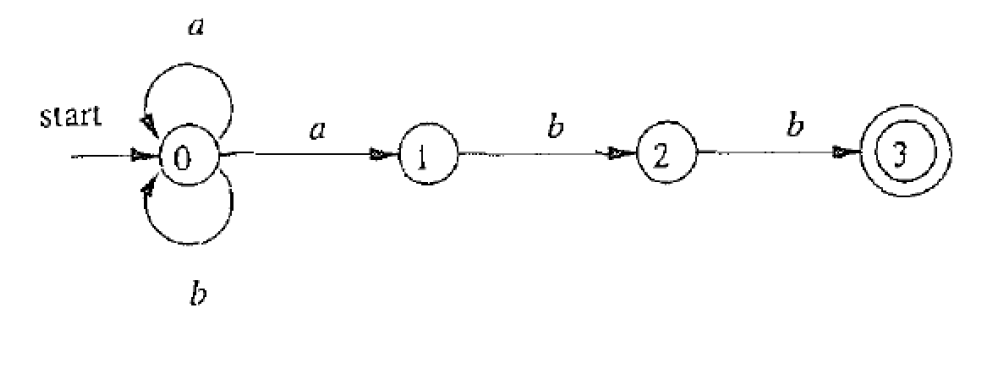
双圈表示接受状态
可以同时识别的real和sci的状态图
12 : 碰到other 怎么办?尝试其它词法单元或进入错误处理模块
14, 16, 17 : 碰到other 怎么办?回退, 寻找最长匹配,peek指针也要回退
我们允许合并后的状态转换图尽量读取输入,直到不存在下一个状态为止,然后类似上面所讨论的那样取最长的和某个模式匹配的最长词素。
例如1.2345E+a -> 1.2345 E + a,gcc会直接认为这个字符串是非法的,而我们的词法分析器在词法部分不这么认为(也就是完成划分),也就是在语法阶段拒绝。
关键点 : 合并22, 12, 9, 0, 根据下一个字符 即可判定词法单元的类型否则, 调用错误处理模块(对应other), 报告该字符有误 , 忽略该字符。
注意, 在sci中, 有时需要回退 , 寻找最长匹配。
Fast Lexical Analyzer Generator
输入 : 程序文本/字符串s & 词法单元的规约输出 : 词法单元流
输入 : 词法单元的规约输出 : 词法分析器比较关键的是.l文件
我们需要词法单元的形式化规约
我们需要词法单元的形式化 规约
id : 字母开头的字母/数字串id 定义了一个集合, 我们称之为语言(Language) ,C语言就是使用C语言写出来的所有语言它使用了字母与数字等符号集合, 我们称之为字母表(Alphabet)
该语言中的每个元素(即, 标识符) 称为串(String)
字母表Σ \Sigma Σ
字母表Σ \Sigma Σ Σ \Sigma Σ 有穷 序列。
空串:∣ ϵ ∣ = 0 |\epsilon| = 0 ∣ ϵ ∣ = 0
x = dog, y = house xy = doghouse
s ϵ = ϵ s = s s \epsilon = \epsilon s = s s ϵ = ϵ s = s
s 0 ≜ ϵ s^0 \triangleq ϵ s 0 ≜ ϵ s i ≜ s s i − 1 , i > 0 s^i \triangleq ss^{i-1}, i>0 s i ≜ s s i − 1 , i > 0
语言 是给定字母表Σ \Sigma Σ 可数 的串集合。
∅ ϵ i d : a , b , c , a 1 , a 2 , . . . w s : b l a n k , t a b , n e w l i n e i f : i f \emptyset \\
{\epsilon} \\
id : {a, b, c, a1, a2, . . . } \\
ws : {blank, tab, newline} \\
if : {if} \\
∅ ϵ i d : a , b , c , a 1 , a 2 , . . . w s : b l a n k , t a b , n e w l i n e i f : i f
语言是串的集合,所以所有和集合相关的都可以在语言上操作。
因此, 我们可以通过集合操作构造 新的语言。
后两项显著增强了语言的能力,Kleene闭包是L ∗ L* L ∗ L + L+ L +
L*允许我们构造无穷 集合
L = A , B , . . . , Z , a , b , . . . , z D = 0 , 1 , . . . , 9 L ∪ D 并 集 L D 520 个 元 素 L 4 长 度 为 4 的 字 母 串 L ∗ 所 有 子 母 串 D + 非 空 数 字 串 L ( L ∪ D ) ∗ 标 识 符 i d : L ( L ∪ D ) ∗ L = {A,B, . . . ,Z, a, b, . . . , z} \\
D = {0, 1, . . . , 9} \\
L\cup D 并集\\
LD 520个元素\\
L^4 长度为4的字母串\\
L^* 所有子母串\\
D^+ 非空数字串\\
L(L\cup D)^∗ 标识符 \\
id : L(L \cup D)^∗ \\
L = A , B , . . . , Z , a , b , . . . , z D = 0 , 1 , . . . , 9 L ∪ D 并 集 L D 5 2 0 个 元 素 L 4 长 度 为 4 的 字 母 串 L ∗ 所 有 子 母 串 D + 非 空 数 字 串 L ( L ∪ D ) ∗ 标 识 符 i d : L ( L ∪ D ) ∗
每个正则表达式r 对应一个正则语言L®
正则表达式是语法 , 正则语言是语义
给定字母表Σ \Sigma Σ Σ \Sigma Σ 由且仅由 以下规则定义:
ϵ \epsilon ϵ ∀ a ∈ Σ \forall a \in \Sigma ∀ a ∈ Σ 如果r是正则表达式, 则®是正则表达式;
如果r与s是正则表达式, 则r|s, rs, r∗ 也是正则表达式(这是语法部分)
运算优先级:( ) > ∗ > 连 接 > ∣ () > * > 连接 > | ( ) > ∗ > 连 接 > ∣
( a ) ∣ ( ( b ) ∗ ( c ) ) ≡ a ∣ b ∗ c (a)|((b)*(c))\equiv a|b*c ( a ) ∣ ( ( b ) ∗ ( c ) ) ≡ a ∣ b ∗ c 正则表达式对应的正则语言
L ( ϵ ) = ϵ ( 1 ) L ( a ) = a , ∀ a ∈ Σ ( 2 ) L ( ( r ) ) = L ( r ) ( 3 ) L ( r ∣ s ) = L ( r ) ∪ L ( s ) L ( r s ) = L ( r ) L ( s ) L ( r ∗ ) = ( L ( r ) ) ∗ ( 4 ) L(\epsilon) = {\epsilon} (1)\\
L(a) = {a}, \forall a \in \Sigma (2)\\
L((r)) = L(r) (3)\\
L(r|s) = L(r) \cup L(s) \ L(rs) = L(r)L(s) \ L(r*) =(L(r))* (4)\\
L ( ϵ ) = ϵ ( 1 ) L ( a ) = a , ∀ a ∈ Σ ( 2 ) L ( ( r ) ) = L ( r ) ( 3 ) L ( r ∣ s ) = L ( r ) ∪ L ( s ) L ( r s ) = L ( r ) L ( s ) L ( r ∗ ) = ( L ( r ) ) ∗ ( 4 )
示例
Σ = a , b L ( a ∣ b ) = a , b L ( ( a ∣ b ) ( a ∣ b ) ) = a a , a b , b a , b b L ( a ∗ ) = ( L ( a ) ) ∗ = a ∗ = ∅ , a , a a , . . . 前 一 个 ∗ 是 正 则 表 达 式 上 的 , 后 一 个 ∗ 是 闭 包 L ( ( a ∣ b ) ∗ ) = ( L ( a , b ) ) ∗ L ( a ∣ a ∗ b ) = a , b , a b , a a b , . . . \Sigma = {a, b} \\
L(a|b) = {a, b} \\
L((a|b)(a|b)) = {aa, ab, ba, bb} \\
L(a*) = (L(a))* = {a}* = {\emptyset, a , aa, ...}\\
前一个*是正则表达式上的,后一个*是闭包
L((a|b)*) = (L(a, b))*\\
L(a|a*b) = {a, b, ab, aab, ...}\\
Σ = a , b L ( a ∣ b ) = a , b L ( ( a ∣ b ) ( a ∣ b ) ) = a a , a b , b a , b b L ( a ∗ ) = ( L ( a ) ) ∗ = a ∗ = ∅ , a , a a , . . . 前 一 个 ∗ 是 正 则 表 达 式 上 的 , 后 一 个 ∗ 是 闭 包 L ( ( a ∣ b ) ∗ ) = ( L ( a , b ) ) ∗ L ( a ∣ a ∗ b ) = a , b , a b , a a b , . . .
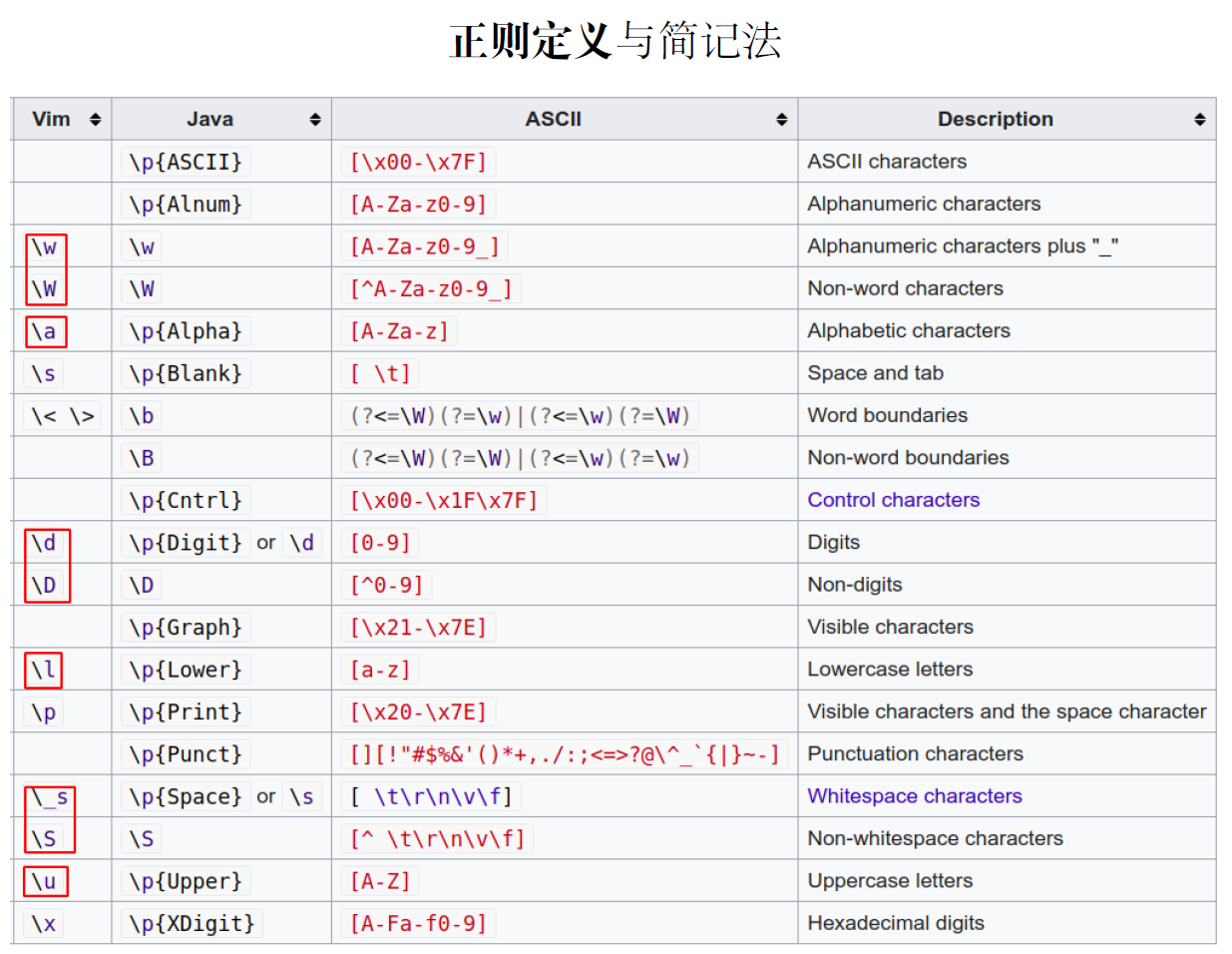
其他常用的:
[^s]:表示不在这个s中的任意一个字符^:外面的尖括号,表示行首$:表示结尾.:除了换行符以外的\c:字符自免租
( 0 ∣ 1 ( 01 ∗ 0 ) 1 ) ) ∗ (0|1(01*0)1))* ( 0 ∣ 1 ( 0 1 ∗ 0 ) 1 ) ) ∗ 正则表达式
声明部分 : 直接拷贝到.c 文件中转换规则 : 正则表达式{动作} 辅助函数 : 动作中使用的辅助函数
最上面我们使用的标准库(原封不动拷贝到lex.yy.c中)
第三部分没有用到
声明部分是可以互相引用的:通过{}来实现、
动作中调用的函数可以在辅助部分使用
yytext是哪里来的呢?flex背后做了很多的事情,需要告诉你做了什么,yytext是flex暴露的全局变量,表示获取到的词素。
1 2 3 flex lexical.l // 生成.yy.c文件
冲突解决 规则
最前优先匹配: 关键字vs. 标识符
最长优先匹配: >=, ifhappy, thenext, 1.23
接受状态可以选择不接受,继续向下匹配
两大要素: 状态集 S S S 状态转移函数 δ \delta δ
根据表达/计算能力 的强弱, 自动机可以分为不同层次:如上图所示,表达能力和计算能力是等价的,组合逻辑(数字逻辑电路)
自动机会对应用于一种语言L ( A ) L(A) L ( A )
L ( A ) ⊆ L ( A ′ ) L(A) \subseteq L(A')
L ( A ) ⊆ L ( A ′ )
无限网格,每一个网格有一个状态
1代表alive,0代表dead
状态转化:根据规则,比如周围八个邻居的当前状态会决定其本身的下一个状态
参考
元胞自动机Gif “生命游戏”(Game of Life) 史诗级巨作
R E ⇒ ϵ − N F A ⇒ N F A RE \Rightarrow \epsilon-NFA \Rightarrow NFA
R E ⇒ ϵ − N F A ⇒ N F A
终点固然令人向往, 这一路上的风景更是美不胜收
非确定性有穷自动A A A A = ( Σ , S , s 0 , δ , F ) A = (\Sigma, S, s_0, \delta, F) A = ( Σ , S , s 0 , δ , F )
字母表Σ ( ϵ ∉ Σ ) \Sigma (\epsilon \notin \Sigma) Σ ( ϵ ∈ / Σ )
有穷的状态集合S S S
唯一的初始状态s 0 ∈ S s_0 \in S s 0 ∈ S
状态转移函数δ \delta δ δ : S × ( Σ ∪ ϵ ) → 2 S \delta : S \times (\Sigma \cup {\epsilon}) \rightarrow 2^S δ : S × ( Σ ∪ ϵ ) → 2 S
接受状态集合F ⊆ S F \subseteq S F ⊆ S
约定: 所有没有对应出边的字符默认指向一个不存在的空状态 :∅ \emptyset ∅
P和NP:NP(Nondeterministic)
“which introduced the idea of nondeterministic machines , which has proved to be an enormously valuable concept.”
(非确定性) 有穷自动机是一类极其简单的计算 装置
它可以识别(接受/拒绝)Σ \Sigma Σ
(非确定性) 有穷自动机A A A x x x s 0 s_0 s 0 f ∈ F f\in F f ∈ F x x x
因此, A A A L ( A ) L(A) L ( A )
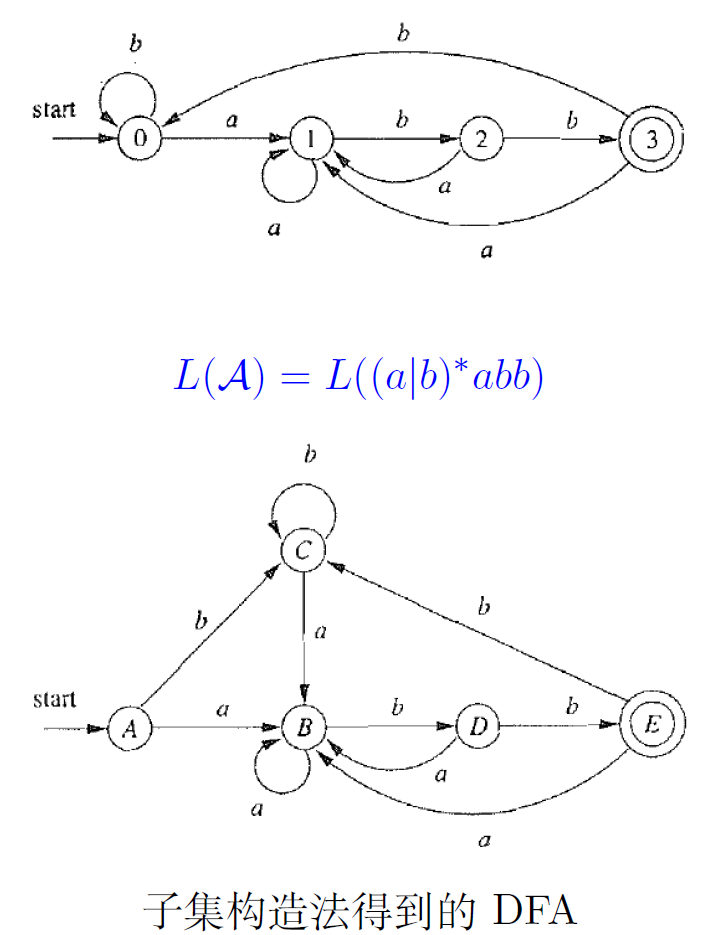
a a b b ∈ L ( A ) a b a b a b ∉ L ( A ) L ( A ) = L ( ( a ∣ b ) ∗ a b b ) aabb \in L(A) \\
ababab \notin L(A) \\
L(A) = L((a|b)^∗abb)
a a b b ∈ L ( A ) a b a b a b ∈ / L ( A ) L ( A ) = L ( ( a ∣ b ) ∗ a b b )
Membership 问题: 给定字符串x x x x ∈ L ( A ) x \in L(A) x ∈ L ( A )
L ( A ) L(A) L ( A )
a a a ∈ A ? 可 以 被 接 受 a a b ∈ A ? 不 可 以 被 接 受 L ( A ) = L ( ( a a ∗ ∣ b b ∗ ) ) aaa \in A? 可以被接受\\
aab \in A? 不可以被接受\\
L(A) = L((aa^∗|bb^∗)) \\
a a a ∈ A ? 可 以 被 接 受 a a b ∈ A ? 不 可 以 被 接 受 L ( A ) = L ( ( a a ∗ ∣ b b ∗ ) )
ϵ \epsilon ϵ
1011 ∈ L ( A ) ? 不 包 含 0011 ∈ L ( A ) ? 包 含 L ( A ) = 包 含 偶 数 个 1 或 偶 数 个 0 的 01 串 1011 \in L(A)? 不包含\\
0011 \in L(A)? 包含\\
L(A) = {包含偶数个1或偶数个0的01串}
1 0 1 1 ∈ L ( A ) ? 不 包 含 0 0 1 1 ∈ L ( A ) ? 包 含 L ( A ) = 包 含 偶 数 个 1 或 偶 数 个 0 的 0 1 串
确定性有穷自动机A A A A = ( Σ , S , s 0 , δ , F ) A = (\Sigma, S, s_0, \delta, F) A = ( Σ , S , s 0 , δ , F )
字母表Σ ( ϵ ∉ Σ ) \Sigma (\epsilon \notin \Sigma) Σ ( ϵ ∈ / Σ )
有穷的状态集合S S S
唯一的初始状态s 0 ∈ S s_0 \in S s 0 ∈ S
状态转移函数δ \delta δ δ : S × Σ → S δ : S \times \Sigma \rightarrow S δ : S × Σ → S Σ \Sigma Σ
接受状态集合F ⊆ S F \subseteq S F ⊆ S
约定: 所有没有对应出边的字符默认指向一个不存在的"死状态"
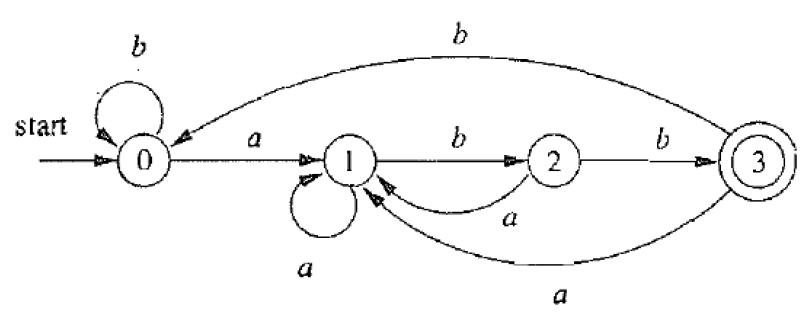
a a b b ∈ L ( A ) a b a b a b ∉ L ( A ) L ( A ) = L ( ( a ∣ b ) ∗ a b b ) aabb \in L(A) \\
ababab \notin L(A) \\
L(A) = L((a|b)^∗abb) \\
a a b b ∈ L ( A ) a b a b a b ∈ / L ( A ) L ( A ) = L ( ( a ∣ b ) ∗ a b b )
上面的确定性自动机和非确定性自动机是等价的
N F A NFA N F A D F A DFA D F A x ∈ L ( A ) x \in L(A) x ∈ L ( A ) 用N F A NFA N F A D F A DFA D F A
R E ⇒ N F A ⇒ D F A ⇒ 词 法 分 析 器 RE \Rightarrow NFA \Rightarrow DFA \Rightarrow 词法分析器 R E ⇒ N F A ⇒ D F A ⇒ 词 法 分 析 器 以下我们就要将上述的几个算法
R E ⇒ N F A r ⇒ N ( r ) 要 求 : L ( N ( r ) ) ⇒ L ( r ) RE \Rightarrow NFA \\
r \Rightarrow N(r) \\
要求: L(N(r)) \Rightarrow L(r) \\
R E ⇒ N F A r ⇒ N ( r ) 要 求 : L ( N ( r ) ) ⇒ L ( r )
Thompson 构造法的基本思想: 按结构归纳
给定字母表Σ \Sigma Σ Σ \Sigma Σ
ϵ \epsilon ϵ ∀ a ∈ Σ \forall a \in \Sigma ∀ a ∈ Σ a a a 如果s s s ( s ) (s) ( s )
如果s s s t t t s ∣ t s|t s ∣ t s t st s t s ∗ s^∗ s ∗
ϵ \epsilon ϵ
a ∈ Σ a \in \Sigma a ∈ Σ
s ∣ t s|t s ∣ t
如果s s s ( s ) (s) ( s )
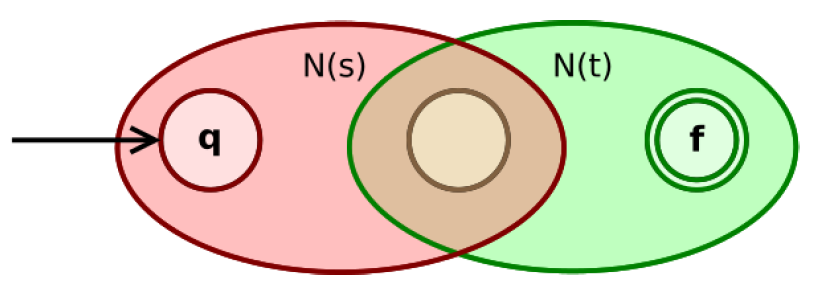
N ( ( s ) ) = N ( s ) N((s)) = N(s) N ( ( s ) ) = N ( s ) 如果s , t s, t s , t s ∣ t s|t s ∣ t
Q:如果N ( s ) N(s) N ( s ) N ( t ) N(t) N ( t )
根据归纳假设 , N ( s ) N(s) N ( s ) N ( t ) N(t) N ( t ) 唯一 :我们的算法是递归构造的,前两种基本情况都为单输入单输出,所以在此基础上构造页必然为单输入单输出
s t st s t
如果s s s t t t s t st s t
根据归纳假设 ,N ( s ) N(s) N ( s ) N ( t ) N(t) N ( t ) 唯一 。
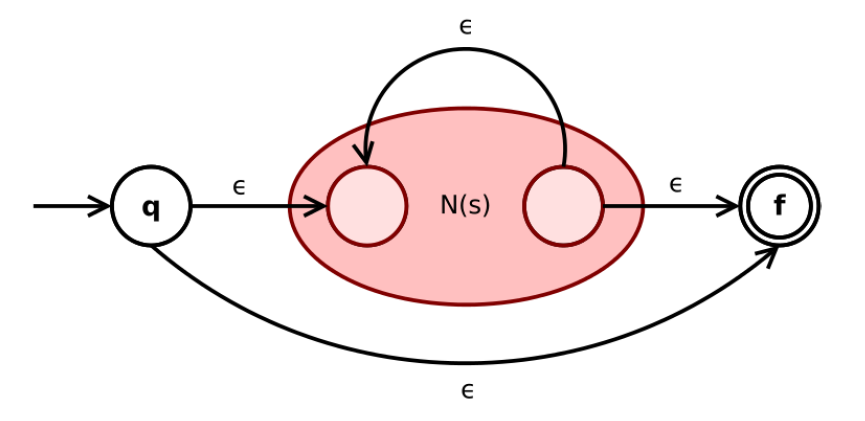
s ∗ s^* s ∗
如果s s s s ∗ s^∗ s ∗
根据归纳假设, N ( s ) N(s) N ( s )
N ( r ) N(r) N ( r )
N ( r ) N(r) N ( r ) 开始状态没有入边, 接受状态没有出边。
(重要)N ( r ) N(r) N ( r ) 状态数 ∣ S ∣ ≤ 2 × ∣ r ∣ |S| \leq 2 × |r| ∣ S ∣ ≤ 2 × ∣ r ∣ ∣ r ∣ : r |r|:r ∣ r ∣ : r
每个状态最多有两个ϵ \epsilon ϵ ϵ \epsilon ϵ
∀ a ∈ Σ \forall a \in \Sigma ∀ a ∈ Σ
N F A ⇒ D F A N ⇒ D 要 求 : L ( D ) = L ( N ) NFA \Rightarrow DFA \\
N \Rightarrow D \\
要求: L(D) = L(N) \\
N F A ⇒ D F A N ⇒ D 要 求 : L ( D ) = L ( N )
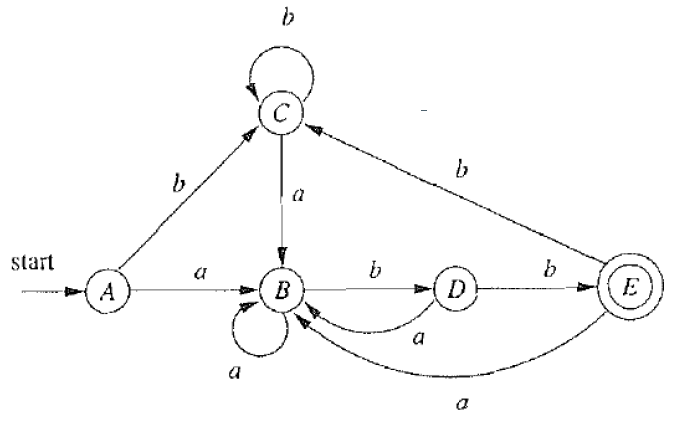
从NFA 到DFA 的转换: 子集构造法(Subset/Powerset Construction)
思想: 用DFA模拟NFA
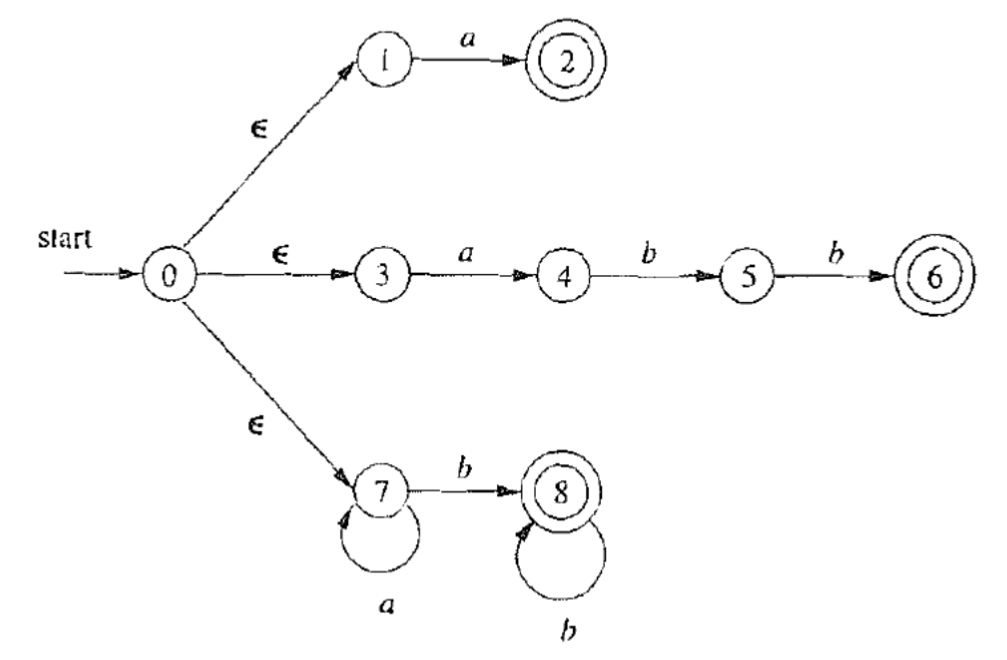
确定初始状态:初始化为A(和0对应),ϵ \epsilon ϵ
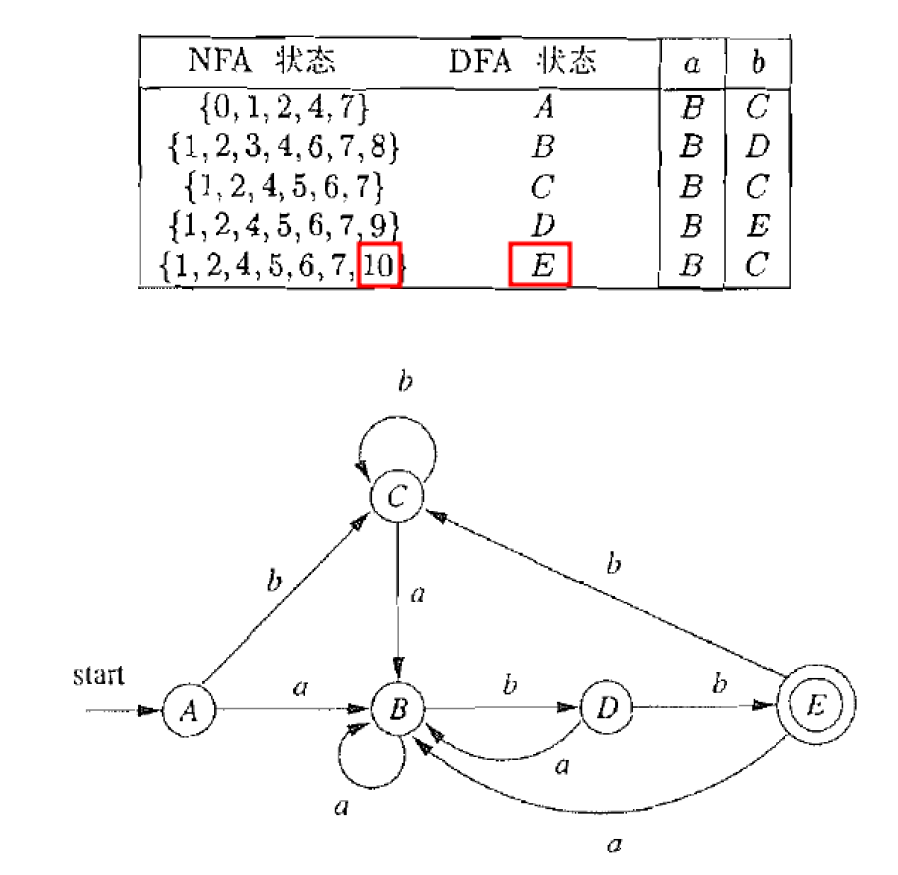
s t e p 1 : A = { 0 , 1 , 2 , 4 , 7 } ⇔ ϵ − c l o s u r e ( 0 ) s t e p 2 : B = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } n o t e : A → N F A a { 3 , 8 } → m o v e ϵ − c l o s u r e B . . . step1: A = \{0, 1, 2, 4, 7\} \Leftrightarrow \epsilon-closure(0) \\
step2: B = \{1, 2, 3, 4, 6, 7, 8\} \\
note: A \xrightarrow[NFA]{a} \{3, 8\} \xrightarrow[move]{\epsilon-closure} B \\
... \\
s t e p 1 : A = { 0 , 1 , 2 , 4 , 7 } ⇔ ϵ − c l o s u r e ( 0 ) s t e p 2 : B = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } n o t e : A a N F A { 3 , 8 } ϵ − c l o s u r e m o v e B . . .
确定接受状态:如果新的状态中包含有一个及以上的原来的接受状态,即为接受状态
E = { 1 , 2 , 4 , 5 , 6 , 7 , 10 } E = \{1, 2, 4, 5, 6, 7, 10\}
E = { 1 , 2 , 4 , 5 , 6 , 7 , 1 0 }
确定转移函数
对 一 个 状 态 : ϵ − c l o s u r e ( s ) = { t ∈ S N ∣ s → ϵ ∗ t } 对 所 有 状 态 : ϵ − c l o s u r e ( T ) = ⋃ s ∈ T ϵ − c l o s u r e ( s ) m o v e 操 作 : m o v e ( T , a ) = ⋃ s ∈ T δ ( s , a ) 对一个状态:\epsilon-closure(s) = \{t \in S_N | s \xrightarrow{\epsilon^*} t\} \\
对所有状态:\epsilon-closure(T) = \bigcup\limits_{s\in T}\epsilon-closure(s) \\
move操作:move(T, a) = \bigcup\limits_{s \in T}\delta(s, a)
对 一 个 状 态 : ϵ − c l o s u r e ( s ) = { t ∈ S N ∣ s ϵ ∗ t } 对 所 有 状 态 : ϵ − c l o s u r e ( T ) = s ∈ T ⋃ ϵ − c l o s u r e ( s ) m o v e 操 作 : m o v e ( T , a ) = s ∈ T ⋃ δ ( s , a )
N = > D N => D N = > D N : ( Σ N , S N , n 0 , δ N , F N ) D : ( Σ D , S D , d 0 , δ D , F D ) Σ D = Σ N S D ⊆ 2 S N ( ∀ s D ∈ S D : s D ⊆ S N ) N : (\Sigma_N, S_N, n_0, \delta_N, F_N)\\
D : (\Sigma_D, S_D, d_0, \delta_D, F_D)\\
\Sigma_D = \Sigma_N\\
S_D \subseteq 2^{S^N} (\forall s_D \in S_D : s_D \subseteq S_N)\\
N : ( Σ N , S N , n 0 , δ N , F N ) D : ( Σ D , S D , d 0 , δ D , F D ) Σ D = Σ N S D ⊆ 2 S N ( ∀ s D ∈ S D : s D ⊆ S N )
初始状态 d 0 = ϵ − c l o s u r e ( s 0 ) d_0 = \epsilon-closure(s_0) d 0 = ϵ − c l o s u r e ( s 0 ) 转移函数 ∀ a ∈ Σ D : δ D ( s D , a ) = ϵ − c l o s u r e ( m o v e ( s D , a ) ) \forall a \in \Sigma_D : \delta_D(s_D, a) = \epsilon-closure(move(s_D, a)) ∀ a ∈ Σ D : δ D ( s D , a ) = ϵ − c l o s u r e ( m o v e ( s D , a ) ) 接受状态集 F D = s D ∈ S D ∣ ∃ f ∈ F N . f ∈ s D F_D = {s_D \in S_D | \exist f \in F_N. f \in s_D} F D = s D ∈ S D ∣ ∃ f ∈ F N . f ∈ s D
子集构造法(N => D) 的实现: 使用栈实现ϵ − c l o s u r e ( T ) \epsilon-closure(T) ϵ − c l o s u r e ( T )
子集构造法(N => D) 的实现: 使用标记搜索过程构造状态集
N ↔ N F A D ↔ D F A ∣ S N ∣ = n ∣ S D ∣ = θ ( 2 n ) 最 坏 情 况 下 , ∣ S D ∣ = Ω ( 2 n ) N \leftrightarrow NFA \\
D \leftrightarrow DFA \\
|S_N| = n \\
|S_D| = \theta(2^n) \\
最坏情况下, |S_D| = \Omega(2^n) \\
N ↔ N F A D ↔ D F A ∣ S N ∣ = n ∣ S D ∣ = θ ( 2 n ) 最 坏 情 况 下 , ∣ S D ∣ = Ω ( 2 n )
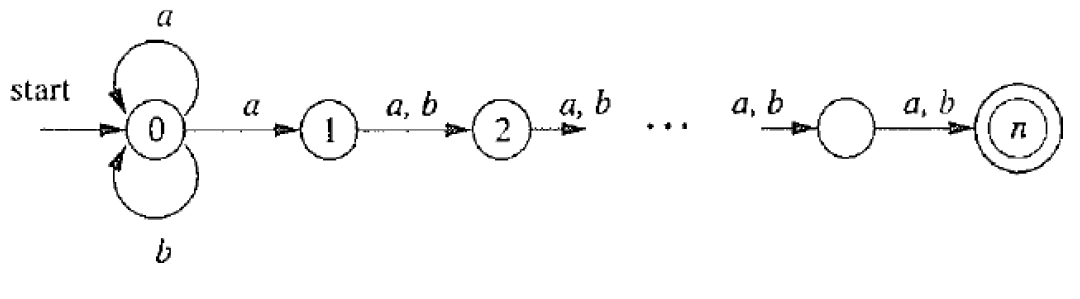
长度为m ≥ n个字符的a,b串, 且倒数第n个字符是a
L n = ( a ∣ b ) ∗ a ( a ∣ b ) n − 1 Ln = (a|b)^∗a(a|b)^{n−1} L n = ( a ∣ b ) ∗ a ( a ∣ b ) n − 1
a,b是一种简写
练习(非作业): m = n = 3 m = n = 3 m = n = 3
f − c l o s u r e ( T ) f-closure(T) f − c l o s u r e ( T ) ϵ − c l o s u r e ( T ) L ∗ = ⋃ i = 0 ∞ L i R + T ⇒ f ( T ) ⇒ f ( f ( T ) ) ⇒ f ( f ( f ( T ) ) ) ⇒ . . . 直 到 找 到 x 使 得 f ( x ) = x ( x 称 为 f 的 不 动 点 ) \epsilon-closure(T) \\
L^∗ =\bigcup\limits_{i=0}\limits^{\infty}L^i \\
R^+ \\
T \Rightarrow f(T) \Rightarrow f(f(T)) \Rightarrow f(f(f(T))) \Rightarrow ... \\
直到找到 x 使得f(x) = x (x 称为 f 的不动点) \\
ϵ − c l o s u r e ( T ) L ∗ = i = 0 ⋃ ∞ L i R + T ⇒ f ( T ) ⇒ f ( f ( T ) ) ⇒ f ( f ( f ( T ) ) ) ⇒ . . . 直 到 找 到 x 使 得 f ( x ) = x ( x 称 为 f 的 不 动 点 )
首先说明一个集合T
然后说明一个函数f作用于T
f(现实空间位置)->地图
f(world) -> 世界地图
f(世界地图) -> 当前地图所占的在世界地图中的局部
…
DFA最小化算法 基本思想: 等价 的状态可以合并for fundamental achievements in the design and analysis of algorithms and data structures
s ∼ t ⇔ ∀ a ∈ Σ . ( ( s → a s ′ ) ∧ ( t → a t ′ ) ) ⇒ ( s ′ = t ′ ) . ∼ : 等 价 ∧ : 同 时 满 足 ( a n d ) s \sim t \Leftrightarrow \forall a \in \Sigma. ((s \xrightarrow{a}s')\wedge(t\xrightarrow{a}t')) \Rightarrow (s' = t'). \\
\sim:等价 \\
\wedge:同时满足(and) \\
s ∼ t ⇔ ∀ a ∈ Σ . ( ( s a s ′ ) ∧ ( t a t ′ ) ) ⇒ ( s ′ = t ′ ) . ∼ : 等 价 ∧ : 同 时 满 足 ( a n d )
如上定义是错误的:
对于有些例子比较松,因为上图是满足条件的,但是不是最小的DFA,下图中A、C、E是等价的,但是接受状态和非接受状态时不可能等价的
对于有些例子过于严格:
c、d、e都是接受状态,我们可以认为是等价的。
根据定义,我们可认为a和b是不等价的
但是根据实际情况(下面的最小化结果,他是等价的)
s ∼ t ⇔ ∀ a ∈ Σ . ( ( s → a s ′ ) ∧ ( t → a t ′ ) ) ⇒ ( s ′ ∼ t ′ ) s ≁ t ⇔ ∃ a ∈ Σ . ( s → a s ′ ) ∧ ( t → a t ′ ) ∧ ( s ′ ≁ t ′ ) s \sim t \Leftrightarrow \forall a \in \Sigma. ((s \xrightarrow{a}s')\wedge(t\xrightarrow{a}t')) \Rightarrow (s' \sim t') \\
s \not\sim t \Leftrightarrow \exist a \in \Sigma. (s \xrightarrow{a} s')\wedge(t \xrightarrow{a} t') \wedge (s' \not\sim t')
s ∼ t ⇔ ∀ a ∈ Σ . ( ( s a s ′ ) ∧ ( t a t ′ ) ) ⇒ ( s ′ ∼ t ′ ) s ∼ t ⇔ ∃ a ∈ Σ . ( s a s ′ ) ∧ ( t a t ′ ) ∧ ( s ′ ∼ t ′ )
根据上面第一个式子,我们不断合并 等价的状态, 直到无法合并为止(闭包的概念)
但是, 这是一个递归定义, 从哪里开始呢?我们使用划分,而不是合并,首先排除终止状态
上图中:A接受a,而B接受ab,上图已经是最小化的
s ≁ t ⇔ ∃ a ∈ Σ . ( s → a s ′ ) ∧ ( t → a t ′ ) ∧ ( s ′ ≁ t ′ ) s \not\sim t \Leftrightarrow \exist a \in \Sigma. (s \xrightarrow{a} s')\wedge(t \xrightarrow{a} t') \wedge (s' \not\sim t')
s ∼ t ⇔ ∃ a ∈ Σ . ( s a s ′ ) ∧ ( t a t ′ ) ∧ ( s ′ ∼ t ′ )
我们根据上面式子进行划分,而非合,不断精化的过程。
对于这个递归定义,我们从哪里开始呢?我们首先将接受状态和非接受状态分开
∏ = { F , S \ F } \prod = \{F, S \backslash F \}
∏ = { F , S \ F }
上式表示进行划分
接受状态与非接受状态必定不等价
空串ϵ \epsilon ϵ
π 0 = { { A , B , C , D } , { E } } π 1 = { { A , B , C } , { D } , { E } } ( b e c a u s e b ) π 2 = { { A , C } , { B } , { D } , { E } } ( b e c a u s e b ) π 3 = { { A , C } , { B } , { D } , { E } } ( b e c a u s e b ) π 2 = π 3 , s o s t o p \pi_0 = \{\{A, B, C ,D\}, \{ E \}\} \\
\pi_1 = \{\{A, B, C\}, \{D\}, \{ E \}\} (because\ b) \\
\pi_2 = \{\{A, C\}, \{B\}, \{D\}, \{ E \}\} (because\ b) \\
\pi_3 = \{\{A, C\}, \{B\}, \{D\}, \{ E \}\} (because\ b) \\
\pi_2 = \pi_3, so \ stop
π 0 = { { A , B , C , D } , { E } } π 1 = { { A , B , C } , { D } , { E } } ( b e c a u s e b ) π 2 = { { A , C } , { B } , { D } , { E } } ( b e c a u s e b ) π 3 = { { A , C } , { B } , { D } , { E } } ( b e c a u s e b ) π 2 = π 3 , s o s t o p
第二步,经过a后仍然还在ABCD中,但是b就可以区分开
第三步,多出了D,导致ABC可能继续细分,还是根据b完成细分
结果如下
∏ = { F , S \ F } \prod = \{F, S \backslash F\} \\
∏ = { F , S \ F }
合并后是一定还是DFA,因为闭包的概念
直到再也无法划分 为止(不动点!)
然后, 将同一等价类里的状态合并
额外报告
如何分析DFA最小化算法的复杂度?
为什么DFA最小化算法是正确的?尝试的action不同,可能会导致结果不同?
最小化DFA是唯一的吗?
如果证明了闭环,我们可以证明正则表达式、NFA和DFA的表达能力是等价的
D F A ⇒ R E D ⇒ r 要 求 : L ( r ) = L ( D ) DFA \Rightarrow RE \\
D \Rightarrow r \\
要求: L(r) = L(D) \\
D F A ⇒ R E D ⇒ r 要 求 : L ( r ) = L ( D )
L ( D ) = { x ∣ ∃ f ∈ F D . d 0 → x f } d 0 表 示 确 定 性 自 动 机 初 始 状 态 r = ∣ x ∈ L ( D ) x e x a m p l e L ( D ) = a , a b , b a r = a ∣ a b ∣ b a L(D) = \{x|\exist f\in F_D. d_0 \xrightarrow{x} f\}\\
d_0 表示确定性自动机初始状态 \\
r =|_{x\in L(D)} x \\
example \\
L(D) = {a , ab , ba} \\
r = a|ab|ba \\
L ( D ) = { x ∣ ∃ f ∈ F D . d 0 x f } d 0 表 示 确 定 性 自 动 机 初 始 状 态 r = ∣ x ∈ L ( D ) x e x a m p l e L ( D ) = a , a b , b a r = a ∣ a b ∣ b a
字符串x x x
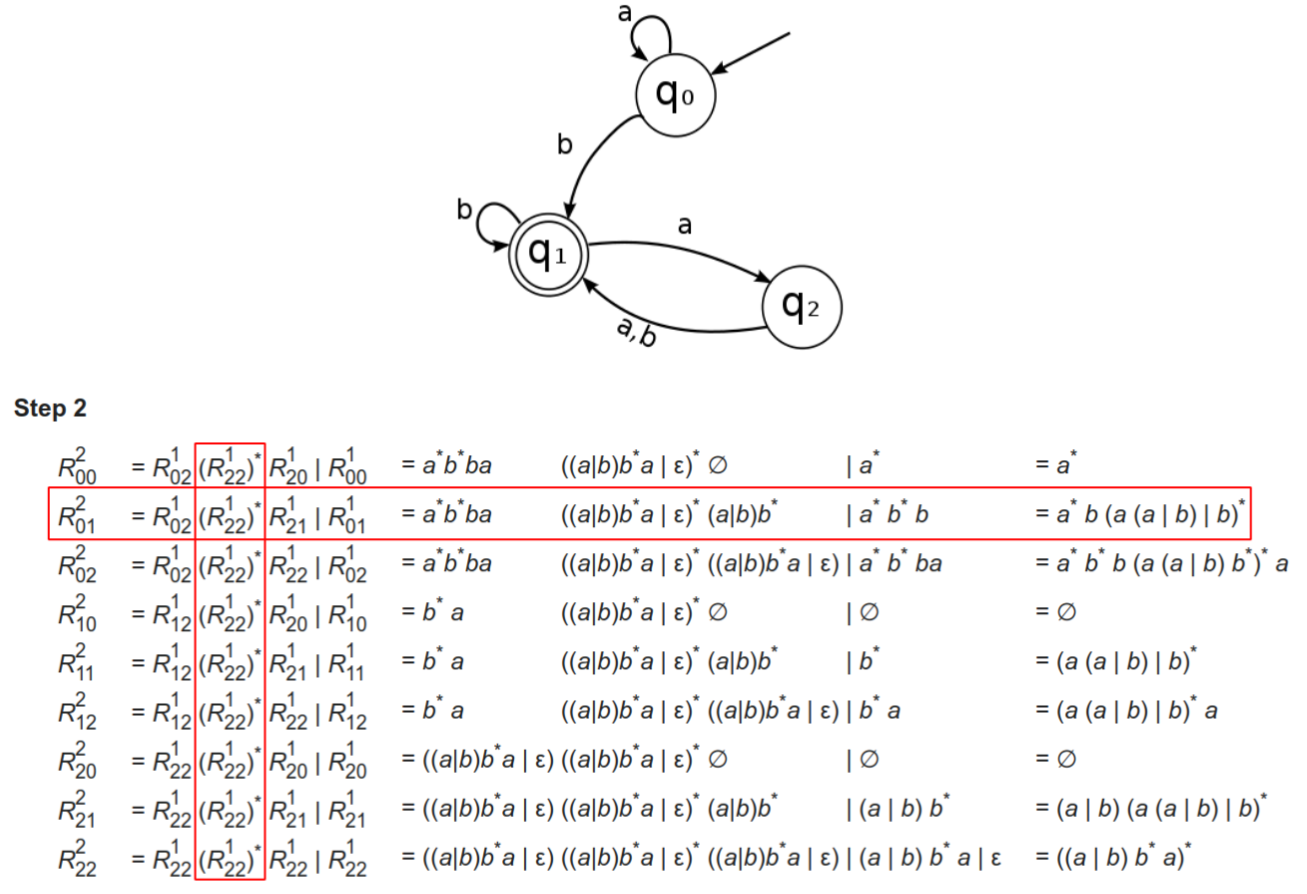
求有向图中所有(从初始状态到接受状态的)路径就可以了,所有点对之间的最短路径(Floyd-warshall算法)
但是, 如果有向图中含有环, 则存在无穷多条路径:我们使用Kleene闭包(添加*)。
假设有向图中节点编号为0(初始状态 )到n − 1,n是所有的状态数。
R i j k R^k_{ij} R i j k 不大于 k的所有路径。
不大于k的所有路径可以将所有路径划分为两种,大问题被讲解为3个小问题。
不经过大于等于k的路径:R i j k − 1 R^{k-1}_{ij} R i j k − 1
经过k的路径:R i k k − 1 、 R k k k − 1 、 R k j k − 1 R_{ik}^{k-1}、R_{kk}^{k-1}、R_{kj}^{k-1} R i k k − 1 、 R k k k − 1 、 R k j k − 1
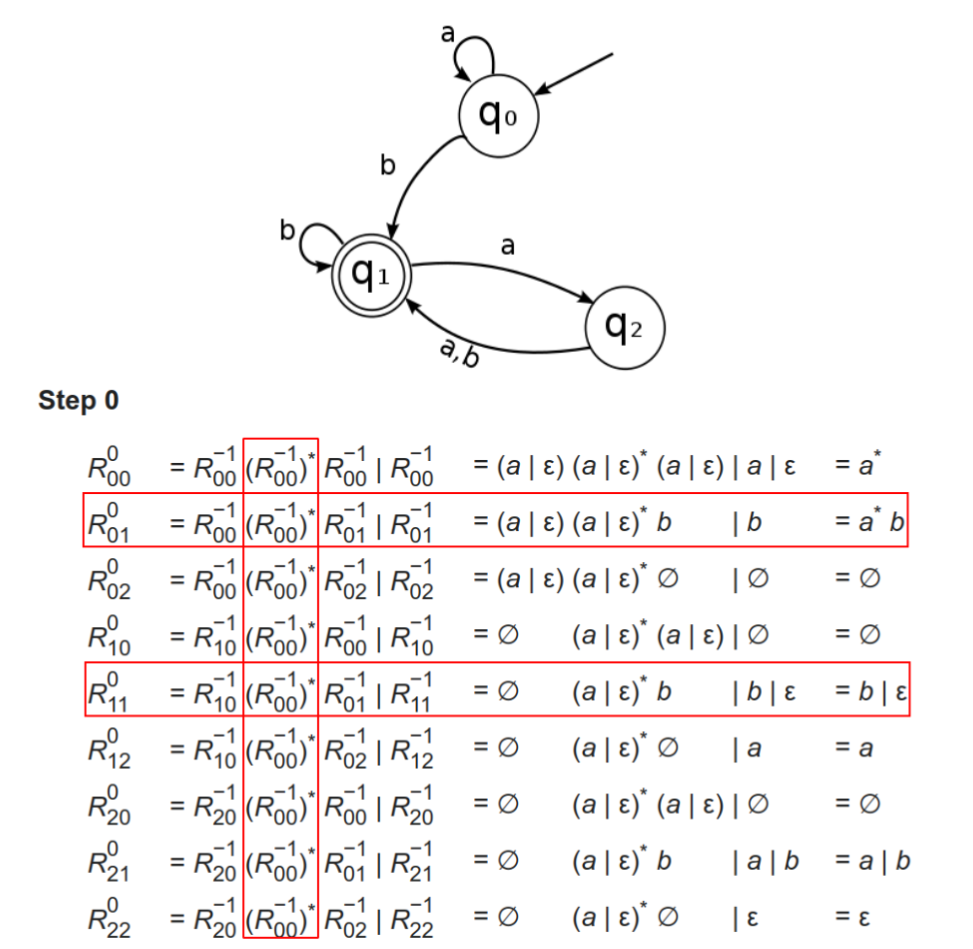
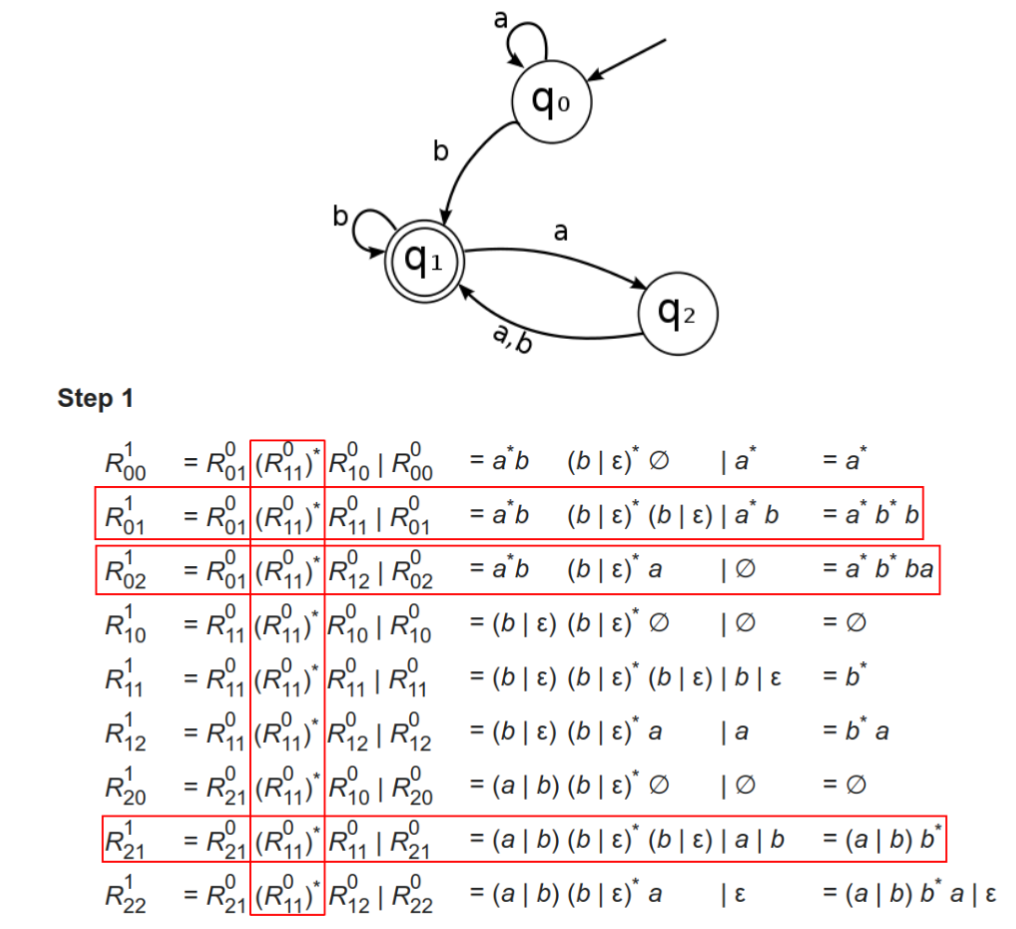
R i j k = R i k k − 1 ( R k k k − 1 ) ∗ R k j k − 1 ∣ R i j k − 1 R_{ij}^k = R_{ik}^{k-1}(R_{kk}^{k-1})^*R_{kj}^{k-1} | R^{k-1}_{ij}
R i j k = R i k k − 1 ( R k k k − 1 ) ∗ R k j k − 1 ∣ R i j k − 1
对于递推关系如何初始化?当k等于0时,我们需要定义一下-1的情况才可以
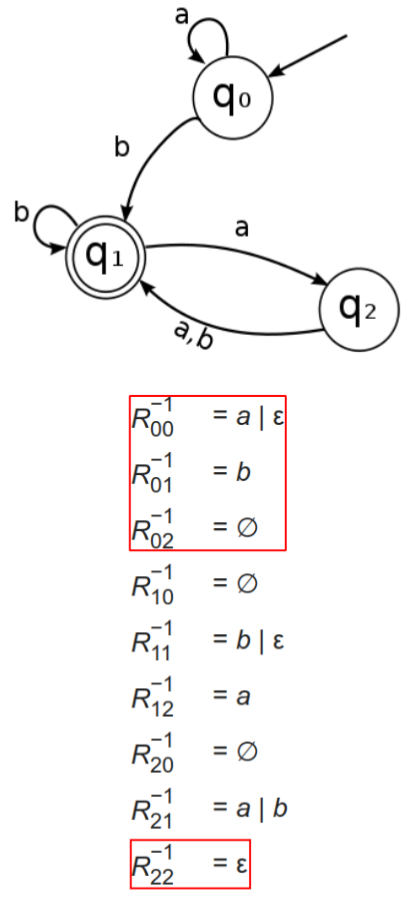
R i j − 1 R_{ij}^{-1} R i j − 1
有直接路径,那么可能i和j之间的直接相连的路径不止一条,使用|连接
有自环:必须要添加ϵ \epsilon ϵ
没有路径:∅ \emptyset ∅
∅ r = r ∅ = ∅ \emptyset r = r \emptyset = \emptyset ∅ r = r ∅ = ∅ ∅ ∣ r = r \emptyset | r = r ∅ ∣ r = r
自己没有自环:ϵ \epsilon ϵ
r的最终结果是什么?
求有向图中所有(从初始状态到接受状态的) 路径:结果如下
∅ \emptyset ∅
r = ∣ s j ∈ F D R 0 j ∣ S D ∣ − 1 r =|_{s_j\in F_D}R_{0j}^{|S_D|-1}
r = ∣ s j ∈ F D R 0 j ∣ S D ∣ − 1
∣ D ∣ |D| ∣ D ∣ ∣ S D ∣ |S_D| ∣ S D ∣ D A D_A D A F D F_D F D
Floyd-warshall算法
Dijkstra算法:一个点到其他点的最短距离
书上写的是不清楚的
a ∣ a b b ∣ a ∗ b + a|abb|a^∗b^+ a ∣ a b b ∣ a ∗ b +
∅ \emptyset ∅
注意:
要保留各个NFA的接受状态 信息,并采用最前优先匹配 原则,保留合并后的状态编号,并且写上对应的接受编码。
如果都匹配,则优先匹配前一个状态,比如68状态先接受的是abb,类比flex中的关键字。
注意去掉死状态:∅ \emptyset ∅
模拟运行该DFA,直到无法继续为止 (输入结束或状态无转移);假设此时状态为s
s为接受状态,识别成功
s为非接受装填,则进行回溯 (包括状态与输入流,一定要同步)至最近一次经过的接受状态,同时回溯指针。
经过最近的接受状态,则识别成功
如果没有经过任何接受状态,则报错 (忽略第一个字符,然后从第二个字符重新开始识别)
无论成功还是失败,都从初始状态 开始继续识别下一个词法单元
当前字符串
识别结果
x=a
输入结束;接受;识别出a
x=abba
状态无转移;接受;识别出abb
x=aaaa
输入结束;回溯成功;识别出a
x=cabb
状态无转移;回溯失败;报错c
有没有可能c在中间呢?具体情况根据DFA的其他接受状态而定
生成DFA后,如果你要进行DFA最小化之后再转化为词法分析器需要注意
初始划分需要考虑不同的词法单元 :首先根据接受情况,现将接受单元进行一步划分。
∏ 0 = { { 0137 , 7 } , { 247 } , { 8 , 58 } , { 68 } } \prod_0=\{\{0137,7\},\{247\},\{8,58\},\{68\}\} ∏ 0 = { { 0 1 3 7 , 7 } , { 2 4 7 } , { 8 , 5 8 } , { 6 8 } } ∏ 1 = { { 0137 } , { 7 } , { 247 } , { 8 } , { 58 } , { 68 } } \prod_1=\{\{0137\},\{7\},\{247\},\{8\},\{58\},\{68\}\} ∏ 1 = { { 0 1 3 7 } , { 7 } , { 2 4 7 } , { 8 } , { 5 8 } , { 6 8 } } 上图已经是一个最小化的DFA了
一道题完成从RE开始的全部