2020-商务智能-Lecture3-OLAP
联机分析处理 OLAP
1. 联机分析处理(OLAP)
1.1. 从联机事务处理(OLTP)到联机分析处理(OLAP)
- 关系数据库模型出现:60年代末E.F. Codd提出的关系数据库模型促进了关系数据库及OLTP的发展
- 数据量大幅度增长:数据量从80年代的M字节及G字节过渡到现在的T字节和P字节
- 性能差异:在这样的数据量的前提下,兼顾事务操作和分析操作在性能上越来越不可能
- 实际情况的不同需求:实际的情况要求为两种目的、特点有很大差异的应用提供不同的解决技术,OLAP应运而生
- OLTP和OLAP是针对两种不同的环境:
- OLTP和关系型数据库相关,面向数据和信息片段
- OLAP是面向完全的信息体的
1.2. OLAP(Online Analytical Processing)
- 通过专门的数据综合引擎,辅之以更加直观的数据访问界面,力图统一分散的公共应用逻辑,在短时间内响应非数据处理专业人员的复杂查询要求。1993年,E.F. Codd将这类技术定义为OLAP
- 短时间:数据仓库做不到短时间响应,不是在线服务
- 非数据处理专业人员:不是所有人都有能力的,访问信息体的过程包含了所有的决策过程,是比较主观的。为什么不配备数据处理专业人员:大量的交流时间
- OLAP(联机分析处理)是针对特定问题的联机数据访问和分析。通过对信息(这些信息已经从原始的数据进行了转换,以反映用户能理解的企业的真实的"维")的很多种可能的观察形式进行快速、稳定一致和交互性的存取,允许管理决策人员对数据进行深入观察
1.3. OLAP vs.OLTP
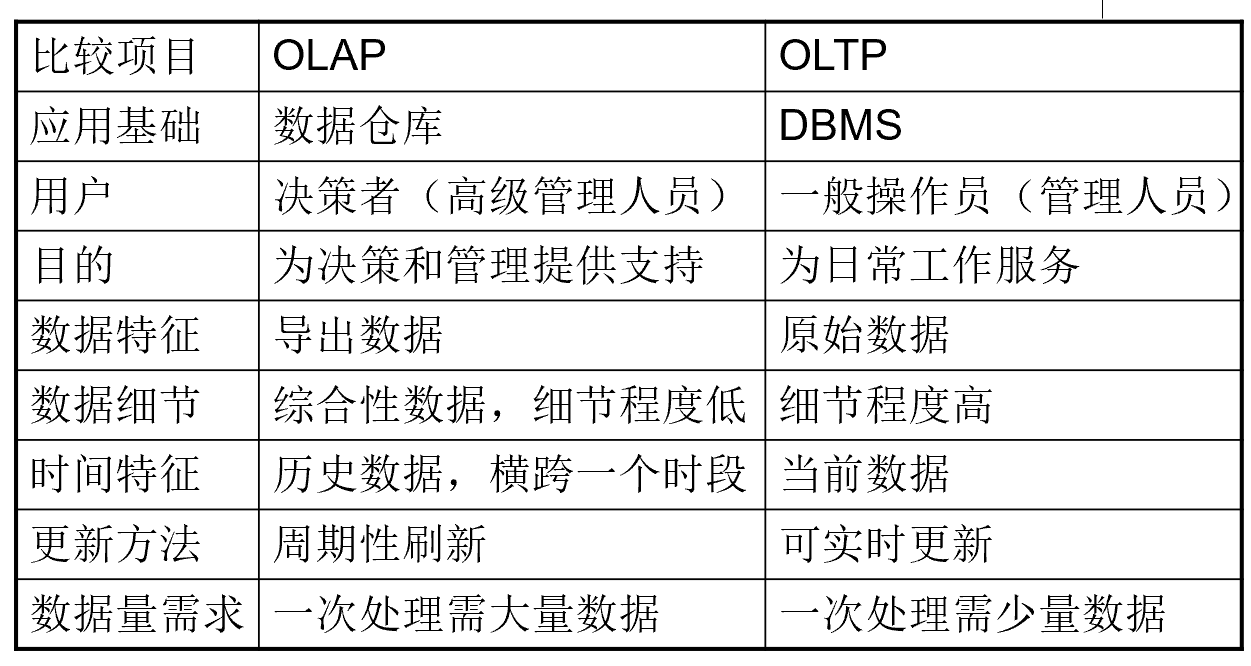
和操作性应用和分析性应用的对比图是相似的
2. OLAP的特征及衡量标准
2.1. Codd关于OLAP的评价准则
2.1.1. OLAP必须提供多维概念视图
从多个维度考察对象:大量情况下,一般是10-15个维度。
2.1.2. 透明性准则
- OLAP在体系结构中的位置对用户是透明的
- OLAP的数据源对用户也是透明的
2.1.3. 存取能力准则
- 将OLAP的概念视图映射到异质的数据存储上,能访问数据并执行所需转换,从而提供单一、完整、连续的用户视图
- 不是客观正确,是主观正确。
2.1.4. 稳定的报表功能
数据的维数和数据的综合层次增加时,提供给最终分析人员的报表能力和响应速度不应该有明显的降低和减慢
2.1.5. 客户/服务器体系结构
- 服务器保证透明性和建立统一的公共概念模式、逻辑模式和物理模式。
- 客户端负责应用逻辑和界面
2.1.6. 维的同等性原则
每一数据维在数据结构和操作能力上都是等同的
2.1.7. 动态的稀疏矩阵处理准则
- OLAP工具必须使得模型的物理模式充分适应指定的维数,尤其是特定模型的数据分布
- 压缩和解压缩:解压缩的时间会不会影响到在线服务,同时要保证空间。
2.1.8. 多用户支持能力准则
OLAP工具必须提供并发访问、数据完整性及安全性机制
2.1.9. 非受限的跨维操作
- 对于多维数据之间存在的固有的层次关系(构成包含的层次关系,比如国家、省市等),OLAP工具应自己推导而不是由用户明确定义相关计算
- 对于无法从固有关系中得出得计算,提供计算完备的语言来定义各种计算公式
2.1.10. 直观的数据操作
2.1.11. 灵活的报表生成
2.1.12. 0
- 维数不应小于15
- 任意聚集层次
2.2. FASMI — 另一个评价准则
FASMI (Fast Analysis of Shared Multidimensional Information)
- Fast:在线
- Analysis:分析是临时起意、规律还是外在的影响
- Shared:多个分析人员使用分时方式来对信息体进行只读的利用
- Multidimensional:多维度,不是按照实现需要、软件需要进行组装,不一定是上下文相关的
- Information:是在信息和信息体层面上的。
3. OLAP中的几个基本概念
3.1. 度量值
度量值,在分析型处理中,我们所关心和分析的对象
- 在多维数据集中,度量值是一组值,而且通常为数字值,比如午饭的花费。
- 度量值是所分析的多维数据集的中心值,即:度量值是最终用户浏览多维数据集时重点查看的数值型数据
- 度量值的选择取决于最终用户所请求的信息类型
- 一些常见的度量值有
- 销售金额 sales
- 成本金额 cost
- 库存数量 production count
- 消费金额 expenditures
- 度量值是主观的,但是受到客观的制约(要但是没有)
3.2. 维
- 维是观察度量值的角度,比如有大量数据与之相关,那么我们需要考虑和观察期内部的联系。
- 例如:可以从三个"维"角度观察销售金额这个度量值
- 时间维:可从时间角度统计(所有)商品在不同时间段内的销售(总)金额,以便于分析其与时间之间的关系
- 商品维:根据商品的分类情况统计每一类商品的销售金额,以便于分析其与商品类型之间的关系
- 地域维:可根据每个连锁店所在的地域统计其销售(总)金额,以便于分析其与地域之间的关系
3.3. 层
- 在分析型应用中,对度量值可以在不同的深度层面上进行分析与观察,并可能得到不同的分析结果。因此,“层” 反映了对度量值的观察深度
- 一般而言,"层"是与"维"相关联的。在一个"维"中可允许存在若干个"层",并且可以采用多种不同的"层"次划分方法
- 维中的"层"通常被组织成一个层次结构,在数据仓库系统的元数据中需要记录不同"层"之间的包含关系,以便于能够在数据仓库中已有的统计结果上正确地执行新的统计查询
3.3.1. 时间维中的层次关系
- 日-月-季-年:包含关系,高层次数据可以通过低层次关系计算出来。
- 日-周-年
- 但是我们认为周和月份是没有偏序关系的:有些周是跨月份的。
- 时间维度关联的度量值在不同层次的体现就是之前讲述的不同粒度。
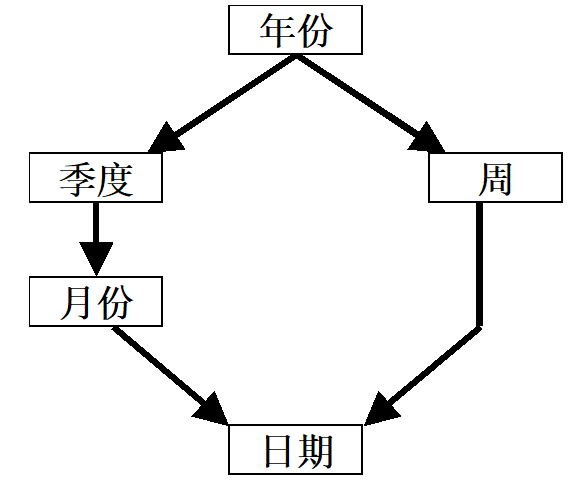
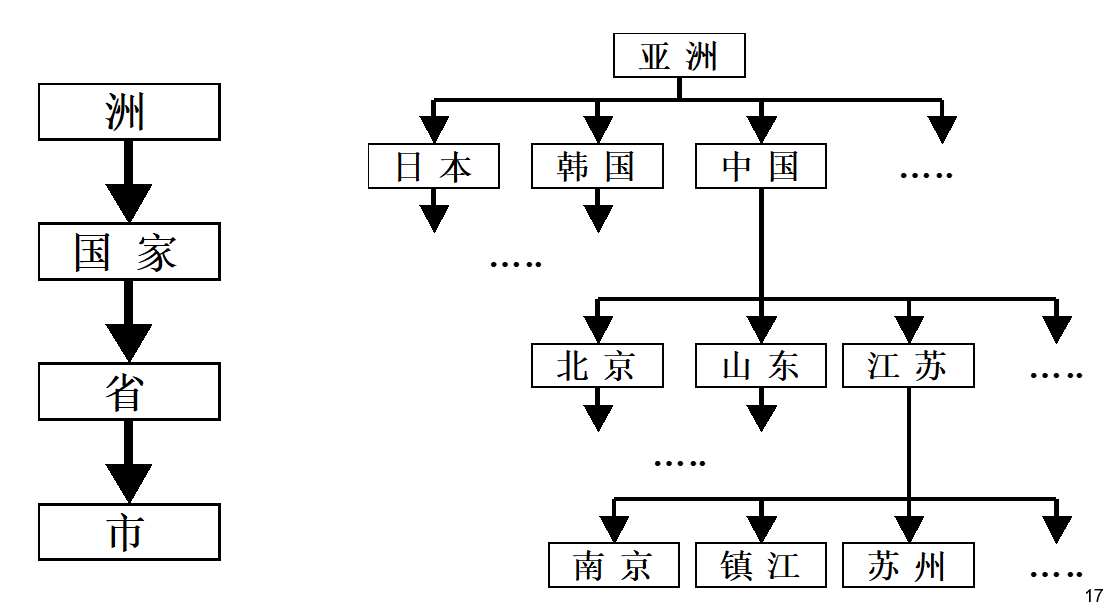
3.3.2. 地域维中的层次关系
- 市-省-国-洲
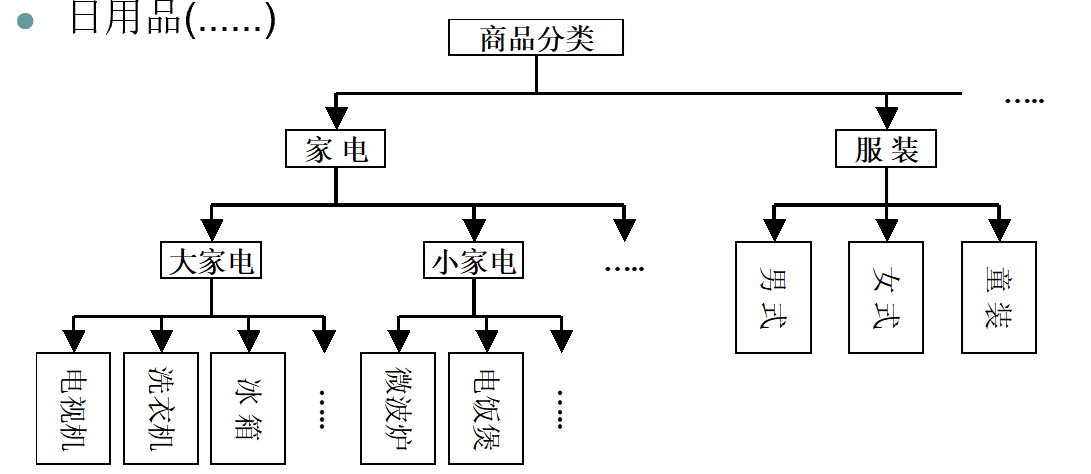
3.3.3. 商品维中的层次关系
- 按商品的类别可以分为
- 家电(大家电(电视机, 洗衣机, 冰箱, …), 小家电(…), …)
- 服装(男式,女式,童装)
- 日用品(…)
- 按如下的方法进行层次划分
- 按商品的价格分为:高档,中档,低档
- 按商品的供应商分为:外资,合资,国营,私营,个体
- 按购买商品的顾客信息划分
- 按照年龄层次来划分:老年,中年,青年,少年儿童,婴儿
- 按照所从事的职业来划分
3.4. 维成员
维的一个取值称为该维的一个"维成员"
- 如果一个维是多层次的,则该维的"维成员"可以是
- 在不同维层次上的取值的组合
- 例如:对具有日,月,年三个层次的"时间维"来说,“某年某月某日”、“某年某月”、“某月某日”、"某年"都是其维成员,如:1998年,1月,1998年1月,1998年1月1日,1月1日
- 这部分代表在这个过程中的维度。
- 在某个维层次上的取值:临时取出作为一个拷贝。
- 例如:“地域"维中的"江苏”,“南京”,…
- 例如:“商品"维中的"电视机”,“服装”,…
- 在不同维层次上的取值的组合
- 对一个度量值来说,维成员是该度量值在某维中位置的描述
3.5. 多维数组
一个多维数组可以表示为(维1, 维2, …, 维n, 变量)
- 其中:
- “变量” 表示我们所观察的度量值
- 维1、维2、…、维n分别表示我们观察该度量值的角度(维)
- 如:(时间,商品种类,商店,销售额)是一个有关商品销售额的三维数组,其中的数据成员可以表示为:
- (2000年,家电,南京市,5000万)
- (2000年7月,女式服装,江苏省,2000万)
- 维度越高,当前的不可用数据就越多。
3.6. 数据单元(单元格)
- 多维数组可以被看成是一个根据多个下标进行定位的值的集合
- 当多维数组的每一维都选中一个维成员,这些维成员的组合就唯一确定了一个度量值,即:(维成员1,维成员2,…,维成员n,度量值)
- 这样一个值或存放该值的地方我们称其为一个"数据单元"
- 可以是实际存在的,也可以是在概念上的一个讨论。
- 数据单元可能是冗余关系,为了保证访问效率。
3.7. 多维数组和联机分析处理
- 假设:在一个分析型应用中需要若干个度量值(设为个), 以它们为聚焦点作不同角度(设每个分析对象有个维)与深度(设每个维上又分为个层)的分析,那么可以得到多种不同的统计分析结果(共为()种),即可以构造出()种多维数组。
- 为了方便快速地查到这些统计分析结果,OLAP需要解决以下两个问题:
- OLAP的数据构造方式
- OLAP的基本数据模型
4. OLAP中的数据构造方式
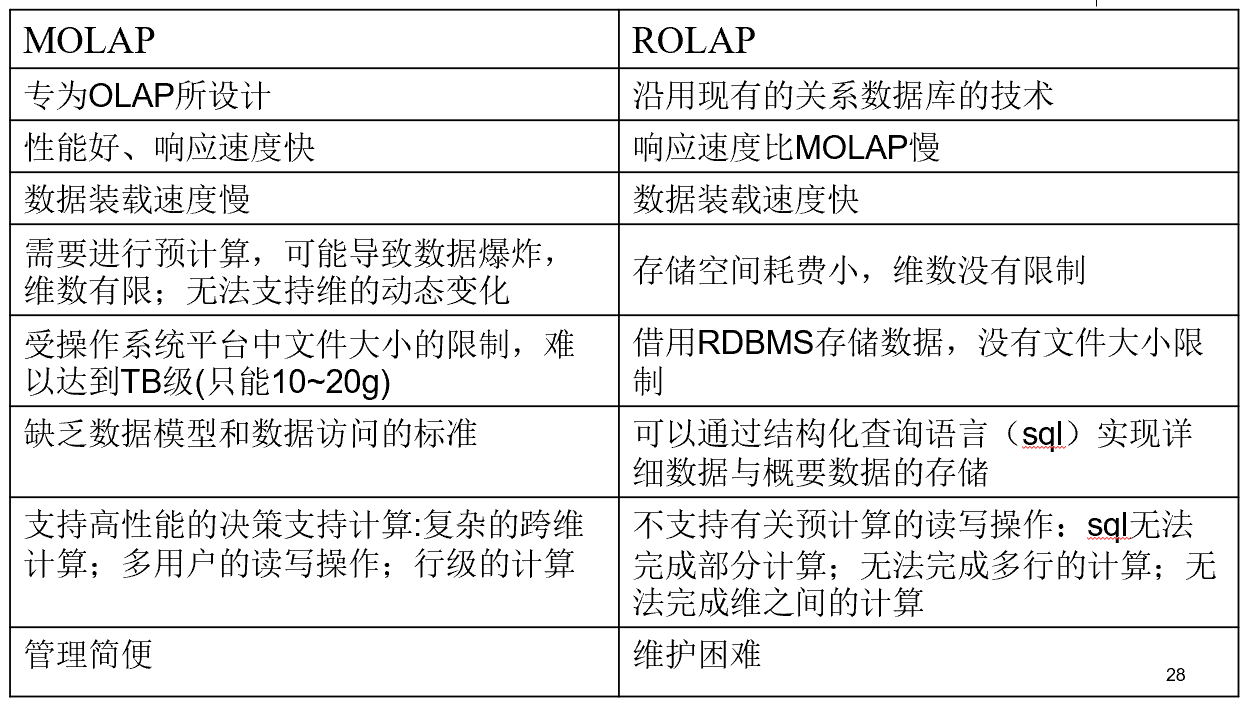
- ROLAP,Relational OLAP
- 用传统的"关系数据库管理系统"(RDBMS)管理,将星型(雪花型)模式用二维表形式存储,表间用关键字相连,从而构成一个关系模式,它称为ROLAP
- 用户在ROLAP上的查询操作将被改写成RDBMS中的查询操作并执行获得查询结果
- MOLAP,Multi-Dimensional OLAP
- 用"多维数据库管理系统"管理,多维数据库采用的基本数据模式就是"多维数组"。
- 在MOLAP中,“事实表"被表示成一个"多维数组”,“维"的属性值被映射成"多维数组"的下标,而"度量值”(包括综合数据)则作为多维数组的取值存储在数据单元中。在查询时,可以通过下标的取值来找到相应多维数组中的"度量值"
- 混合联机分析处理(HOLAP)
4.1. MOLAP 与 ROLAP
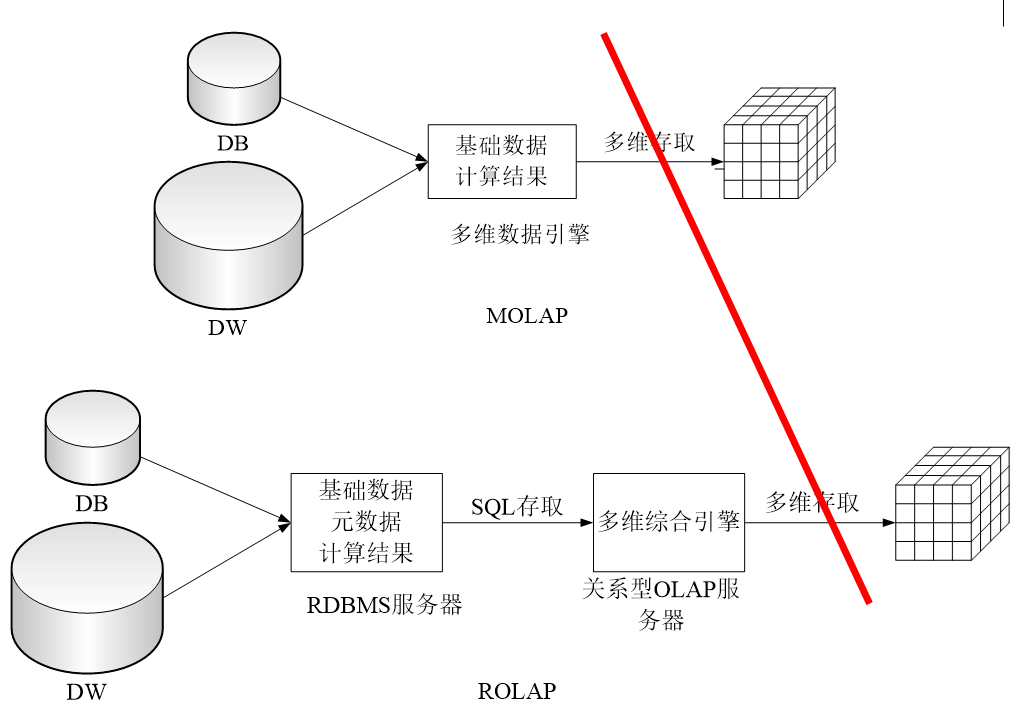
- 结合多维综合引擎作为中介使用
- ROLAP使用关系数据库管理系统(RDBMS)或扩充关系数据库管理系统(XRDBMS)存储和管理数据仓库,以关系表存储多维数据,有较强的可伸缩性。
- 维数据存储在维表
- 事实数据和维ID则存储在事实表
- 维表和事实表通过主键和外键关联。
- 此外,ROLAP通过一些软件工具实现,物理层仍用关系数据库的存储结构,因此称为虚拟OLAP(virtual OLAP)。
- MOLAP支持数据的多维视图,采用多维数组存储数据
- 它把维映射到多维数组的下标或下标的范围
- 事实数据则存储在数组单元中,从而实现了多维视图到数组的映射,形成了立方体(cube)结构。
- 但随着维数的增加,大容量的数据可能使立方体稀疏化,此时需要借助稀疏矩阵压缩技术来处理。由于MOLAP是从物理层实现,采用了多维数组的存储结构,故又称为物理OLAP(physical OLAP)。
4.2. 混合联机分析处理(HOLAP)
- 试图将 MOLAP 和ROLAP进行融合
- 从而在大量数据上获得高效率
- 方式
- 同时提供多维数据库(MDDB)和关系数据库(RDB)
- 将 RDB的查询结果存储到 MDDB
- 使用MDDB存储高层次数据,RDB存储细节数据
- 高层和查询结果使用MOLAP,底层使用ROLAP。
5. OLAP的基本数据模型
5.1. OLAP需解决的问题
- OLAP服务器必须提高对OLAP数据的访问效率,包括:
- 数据抽取、转换及加载的效率:相对没有其他二者不重要,因为是可以离线的。
- OLAP数据查询效率
- OLAP数据更新效率
- 目前可有多种方法以提高ROLAP中的处理效率:
- 采用物化视图方式:存储物化视图,之后就可以直接调用,将视图这种"虚表"形式转换成实际存在的二维表,以达到快速取得综合数据的目的
- 采用特殊的索引与集簇方式,以加速星型模式内表的联接速度
- 尽量采用并行操作方式以提高处理速度
- 采用OLAP中的查询优化技术,如共享排序技术等
- 采用增量技术,在OLAP数据更新时保留不变的数据,仅更改变动的数据以加快数据更新速度
5.2. OLAP的基本数据模型
- MOLAP,多维数据库(MDDB,Multi-Dimensional Database)
- ROLAP,常用的两种ROLAP数据模型
- 星形模型
- 雪花模型
5.3. MDDB vs. RDBMS
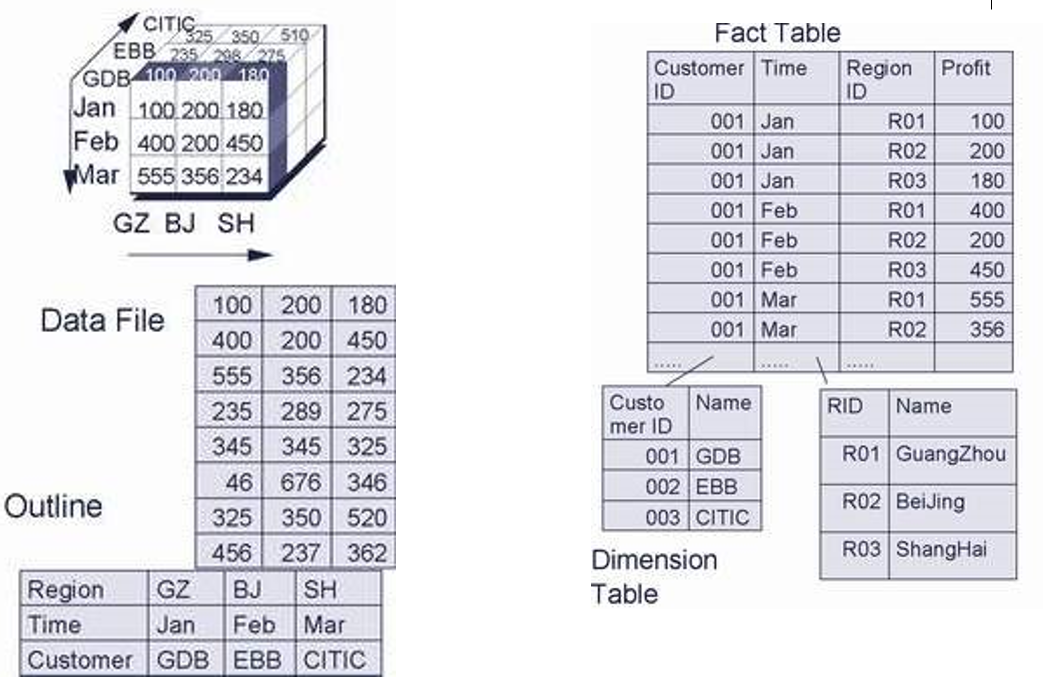
- 左上角是一个三维立体数据模型,每一个块上标注的为对应的数据。
- 地理维度:广州、北京、上海
- 时间维度:一月、二月、三月
- 顾客维度:GDB、EBB、CITIC
- 大量的数据中可能蕴涵非常多的稀疏数据带来了空间浪费的问题
- 左侧为多维数据模型,右侧为二维数据模型。
- 二维数据表可以被拆分为多个表格,之后通过拼接得到最后的大表格,但是我们仍然要考虑冗余的问题和时间效率的问题。
- 维度数等价于关系型数据库的关键字数。
5.4. 多维联机分析处理(MOLAP)
- MOLAP使用专门的多维数据库来存放所需要的数据
- 数据以多维的方式存放,并且使用多维的方式进行展现。
- 多维数组比关系数据表表达更清晰且占用存储小(在处理稠密数据时)
- 高速的综合速度,MOLAP适用于需要高速处理的复杂分析
- 维护多维数组需要大量资源
5.4.1. 多维数据库存取
- 经压缩的、类似于数组的对象构成
- 这些对象带有高度压缩的索引及指针结构
- 并非维间的每种维成员组合都对应合理的度量值,MDDB必须具有高效的稀疏数据处理能力,能略过零元、缺失和重复数据
5.4.2. 使用多维查询语言MDSQL
- 列出1996年1月至6月彩电在北京地区的销售量和成本
- 语法1

- 语法2

5.5. 关系联机分析处理(ROLAP)
- ROLAP使用通用的关系数据库来存储所需数据
- ROLAP 适应于处理大量数据,低效率
- 现有的关系型数据库已经对OLAP做了很多优化,包括并行存储、并行查询、并行数据管理、基于成本的查询优化、位图索引、SQL的OLAP扩展(cube, rollup)等,性能有所提高
5.5.1. 二维数据模型

- 计算上限和下限,上限为销售商、发货、顾客和产品。
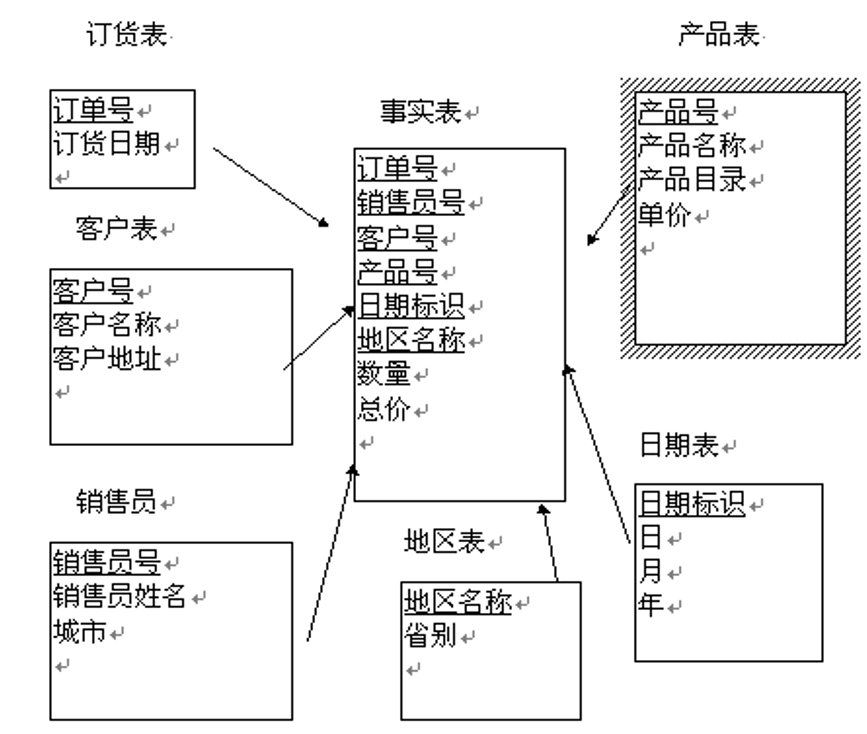
5.5.2. 星型模式
- 星型模式是一种多维表结构,它一般由两种不同性质的二维表组成:
- 事实表(Fact table):存放多维表中的主要事实,称为度量值(Measure)
- 维表(Dimension Table):存放多维表中的维成员的取值
- 一般一个n维的多维表往往有n个维表和一个事实表,它们构成了一个星形结构,因而称其为"星型模式":在星型模式中主体是事实表,而有关维的细节则放置于维表内以达到简化事实表的目的,事实表与维表间由公共属性相连以使它们构成一个整体
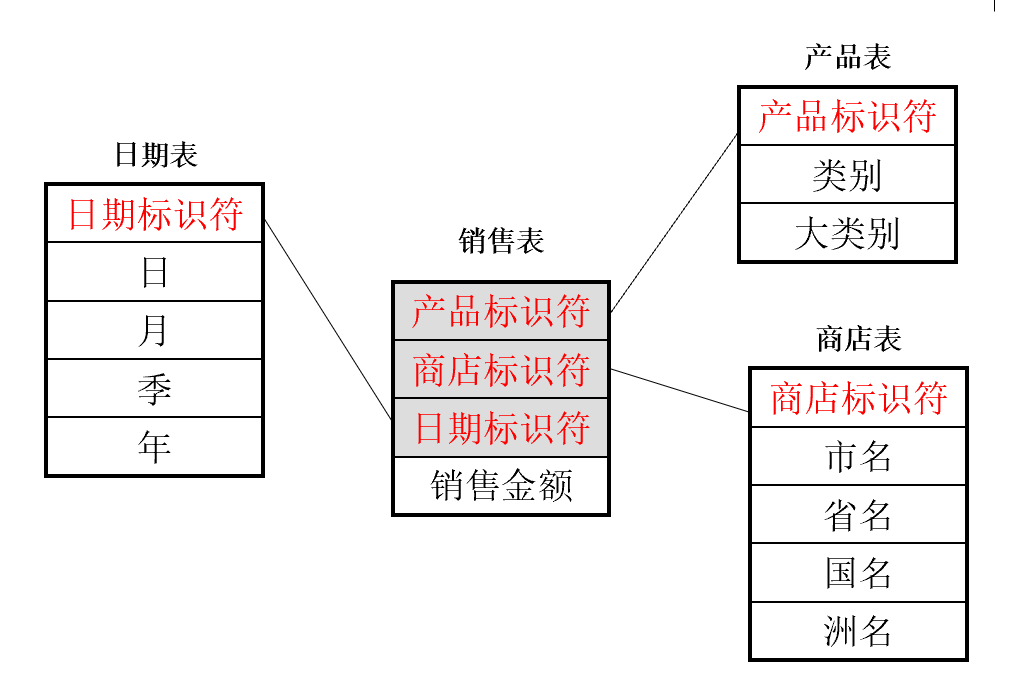
- 上述的星型模式可以转化成下面的四个关系
1 | |
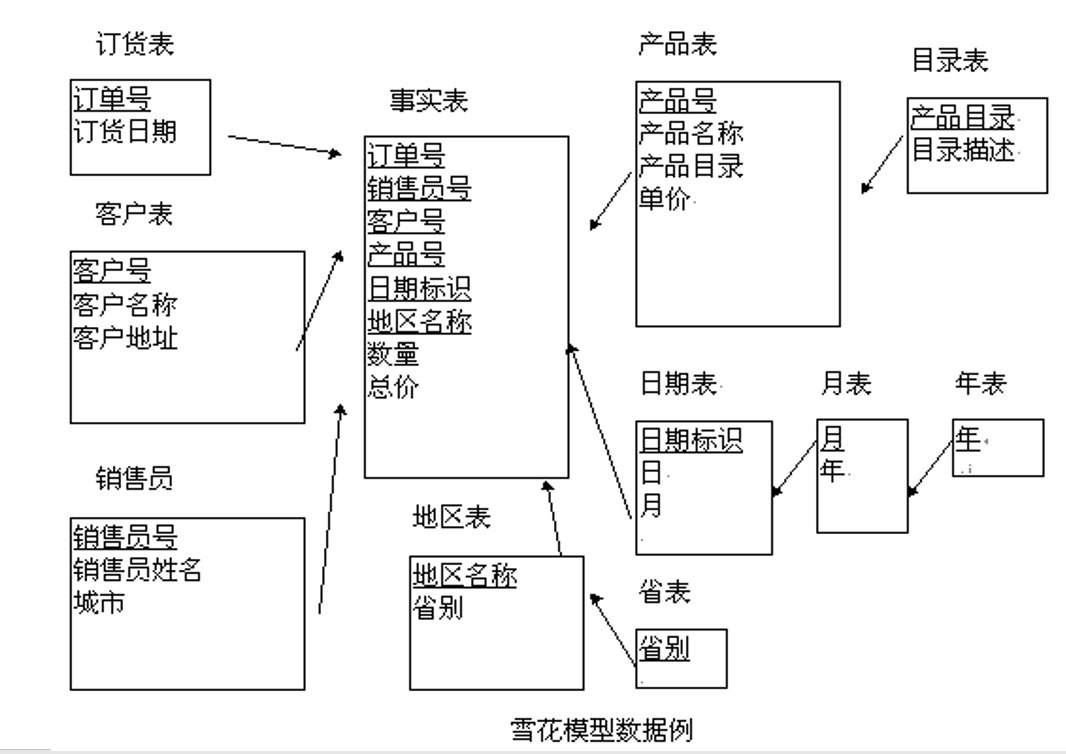
5.5.3. 雪花模式
- 雪花模型是对星型模型的扩展:雪花模型对星型模型的维表进一步层次化,原有的各维表可能被扩展为小的事实表,形成一些局部的"层次"区域
- 优点:使维表尽可能地规范化,最大限度地减少维表的数据存储量
- 缺点:执行查询时需要更多的连接操作,可能会影响查询性能
- 例如:前面的维表1"产品表"也可以是一个如下所示的星型结构:产品(类别,供应商,顾客)
- 在前面的"星型模式"中,我们只考虑产品的分类("类别"属性),在这里我们还可以从产品的"供应商"或"购买顾客"角度来考虑对产品进行分析
- 也可以以其中的"供应商"为中心再构成一个 “星型模式”
产品维表示例

雪花模型示例
- 我们用雪花模型替代星型模型。
- 在当前构造数据模型时,我们会有数据总线:这就是伪表的共享问题。
5.6. 其他扩展模型
- 星座模式:通过公共维度连接多个星型模式

- 雪暴模式:通过公共维度连接多个雪花模式

6. 数据立方体(Data Cube)
6.1. 数据立方体
- 数据仓库的数据模式通常可以看成是定义在多个数据源上的数据视图,其中存储的分析型数据通常是一些经过统计而获得的综合性数据:
- 获取这些综合性数据的常用方法是在视图中用统计函数进行计算,但这种方法的缺点是显见的:时间开销太大
- 大多数情况下,数据是比较稀疏的
- 对于真实情况下,一般使用数据仓库的数据量都不会太小,不然也没有必要使用数据仓库。
- 物化视图
- 为了提高对统计信息的查询速度,我们可以预先计算好数据视图中的统计信息并保存在数据仓库中,这称为物化视图,即将虚的视图转变成实际的视图
- 其本质类似于使用空间来代换时间,可以较好地提高数据仓库的性能。
- 存放物化视图的三维数据模型叫"数据立方体",可以选择物化全部视图并存储。
- 以前面的星型模式为例,其事实表共有三维,即产品P(product)、商店S(store)及日期D(Date),可以为它们定义一系列的物化视图。
PSD视图

PS、SD、PD视图:采用类似的方法也可以定义出SD、PD视图

P、S、D视图:采用类似的方法也可以定义出S、D视图。

ALL视图:ALL视图表示不分组,该视图中的销售总额表示销售表中所有销售金额之和。其定义如下:

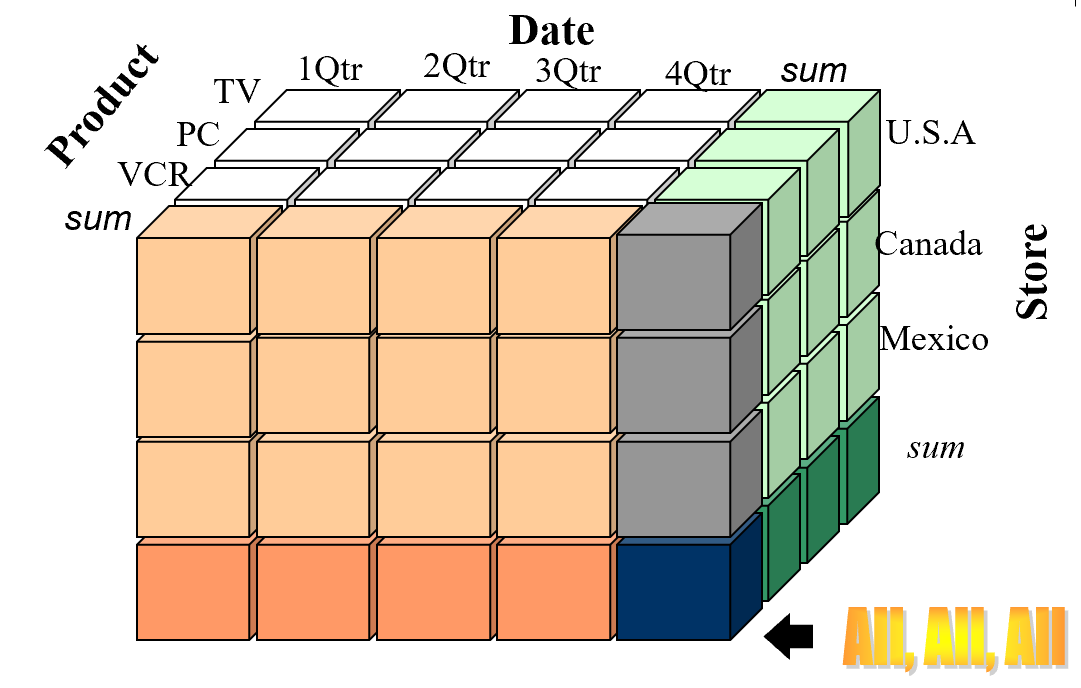
- 如果不考虑层次问题,只考虑维度问题,那么我们可以得到上图中的白色部分
- 关于维度的缩减:而其他颜色的部分,我们对维度进行压缩,得到了sum部分,而最右下角的则是All,All,All视图
6.2. 数据超立方体
- 在数据立方体中进行的是一个三维的分析应用。但当应用中分析对象超过三维时,则构成一个多维(或称n维, n≥4)应用,此时无法用数据立方体表示其中的数据,而只能通过虚拟的n(n≥4)维空间建立n维立方体,它称为"数据超立方体",一般主要针对数据立方体进行讲述。
四维:如图,数据立方体线性排列
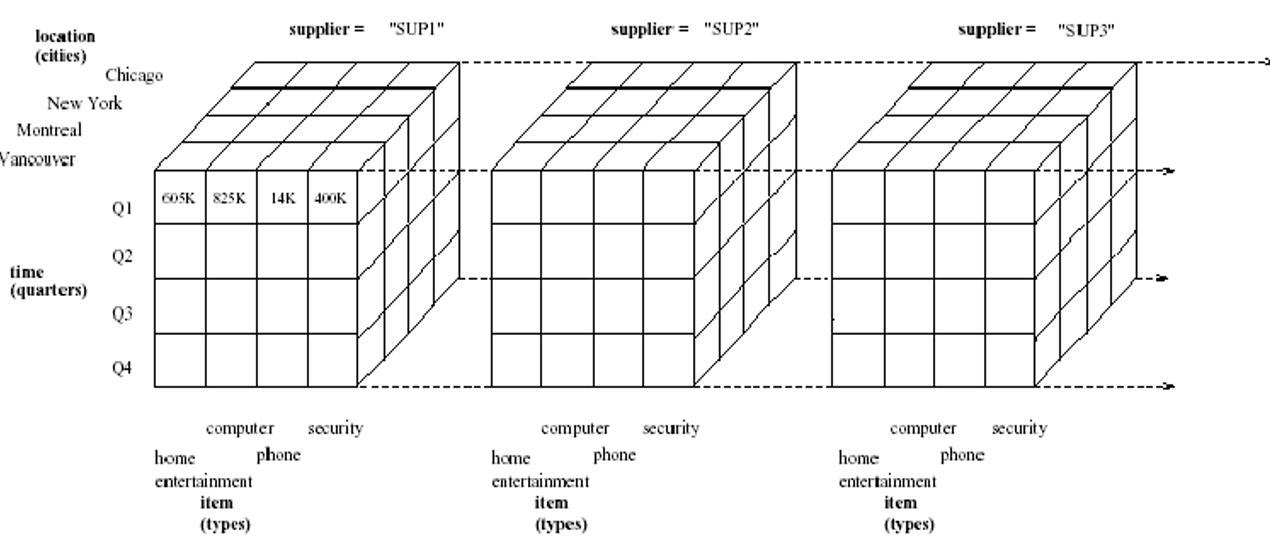
六维:如图,数据立方体成立方体排列
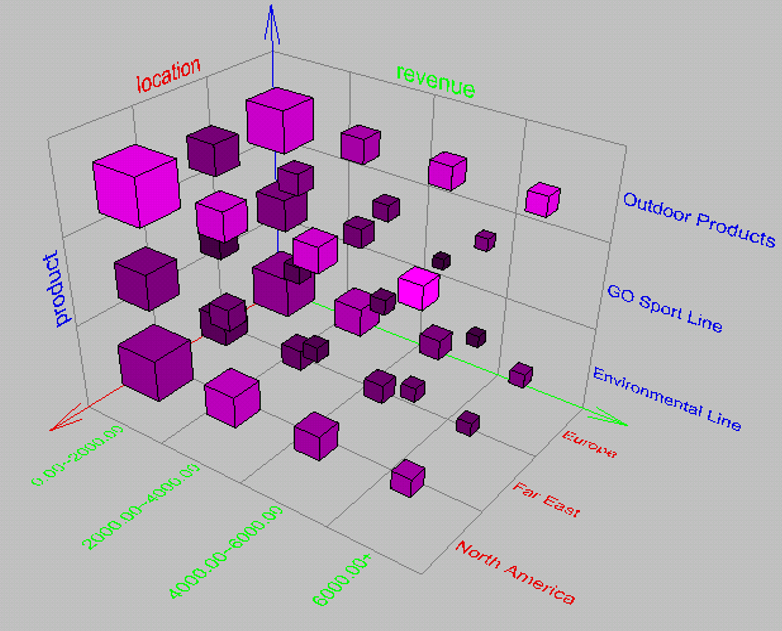
6.3. 方体格
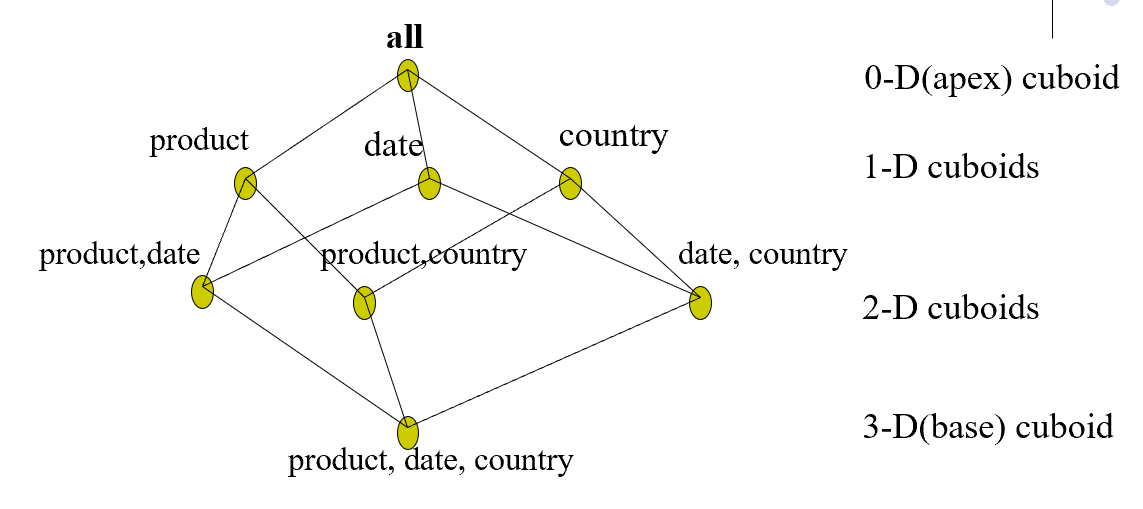
- n维方体称为基本方体
- 0维方体代表最高层次的抽象,称作顶点方体
- 方体格构成数据立方体
- 每一个顶点都是一个方体,对应了一种的可能表达形式
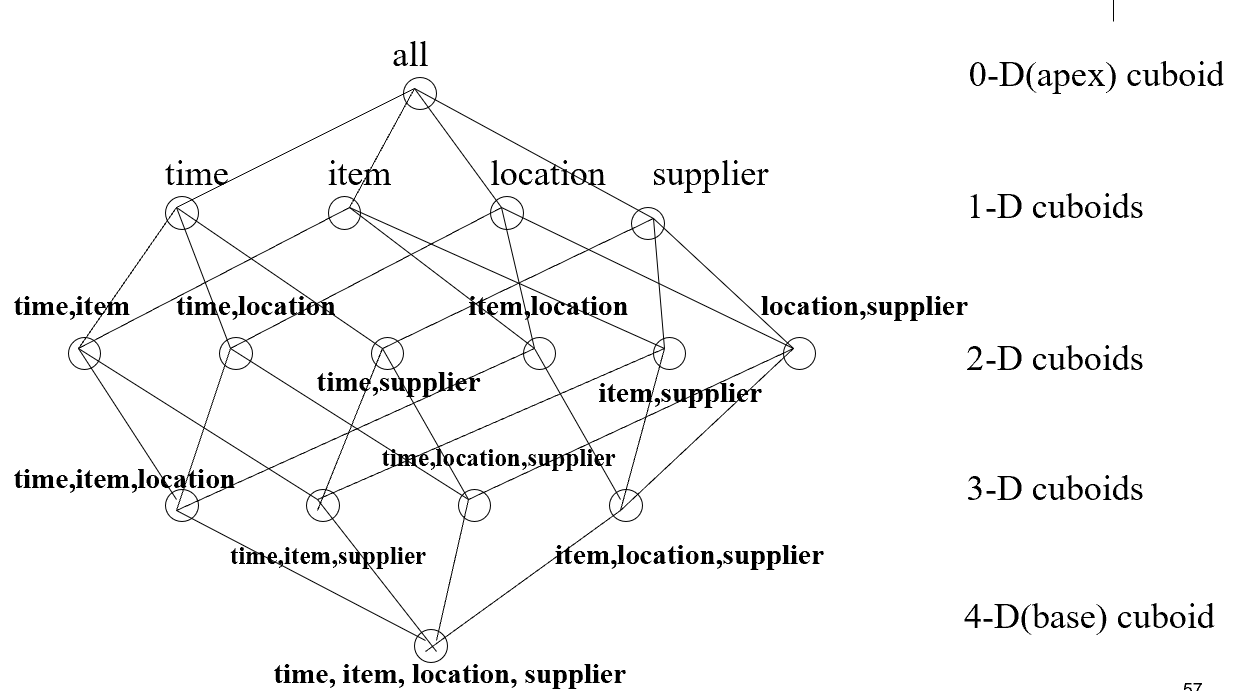
- 上图是4D方体
- 2D方体是4D方体的一个点
- 从下向上可以计算,但是不可以从上向下处理
- 使用格结构,我们可以发现上层资源计算如果底层有部分物化,则不需要从最底层开始计算
6.4. 星型网查询模式
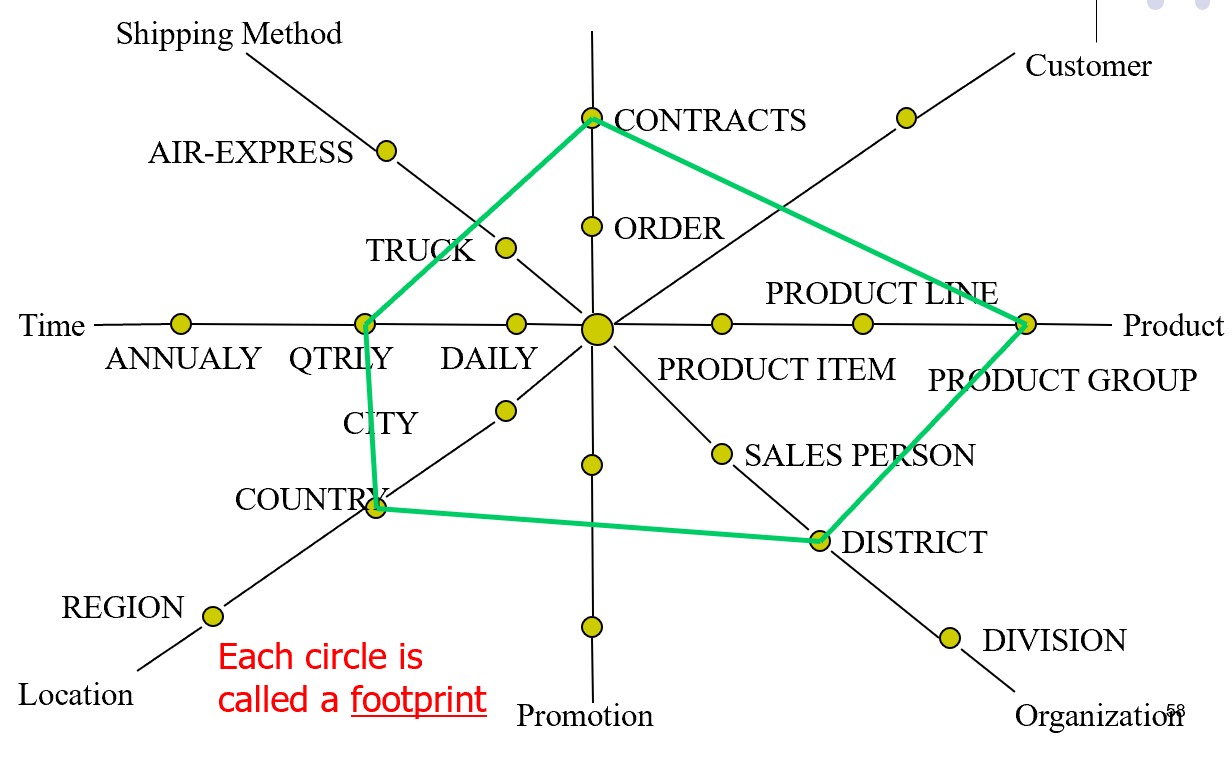
- 在每一个维度里面,我们还应当一并应用层次来进行查询。
- 每一个环我们都称为是一个足迹
6.5. 数据立方体的物化
- 不进行物化
- 全物化:n维 L层的立方体包含种子方,之所以加1是因为包含了All层次
- 部分物化
- 确定要物化的方体子集:
- 冰山方体:比如A集合的数据是远远大于B集合的,那么我们可能会物化A集合的底层节点,或者是我们发现某一个维度可能被经常使用,我们可以选择物化其中的部分。
- 部分物化:因为存储空间是不确定的
- 利用查询处理时物化的方体
- 在装入和刷新时,有效地更新物化的方体
- 确定要物化的方体子集:
6.6. 多维阵列聚合(压缩矩阵)
- 将数组分区成块(块是适合内存的小的子立方体)
- 压缩稀疏数组寻址:(chunk_id,偏移量)
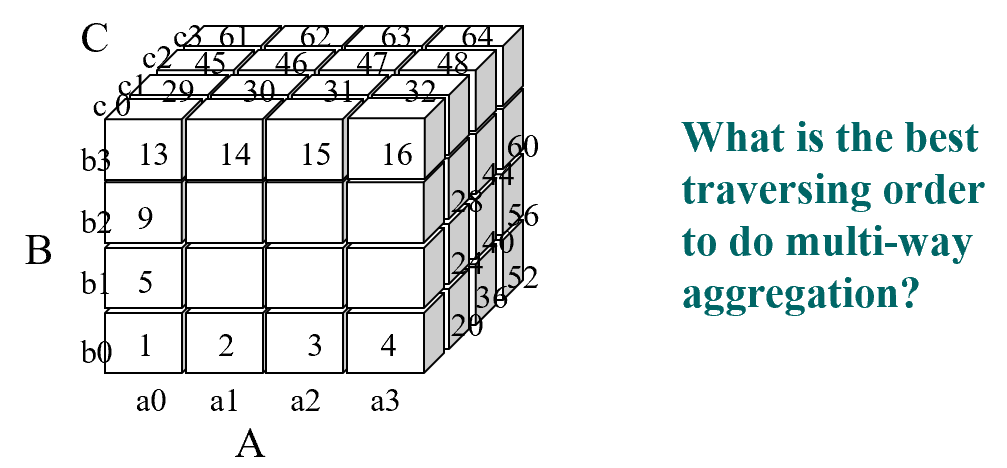
- 通过按以下顺序访问多维数据集单元以"多路"方式计算聚合,该顺序可以最大程度地减少访问每个单元的次数,并减少内存访问和存储成本
- 多维阵列聚合的结果,大概率是无法放置到内存中的
- 导入时间是线性的(我们不讨论并发)
 |
 |
|---|
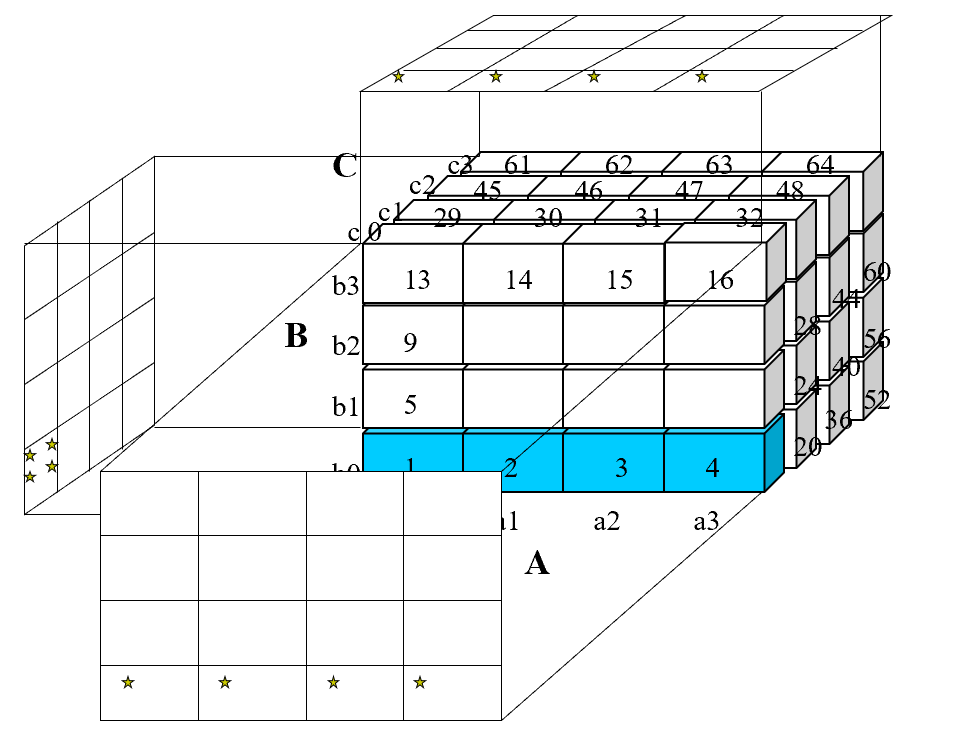
我们需要仔细考虑空间问题:因为空间开销比较大,所以我们开辟了三个2D方体来缓存数据内容

- 左侧空间中,我们得到的数据会顺序落入到对应的位置,上图中有7个星
- 上侧空间中,我们得到的数据会放置到对应的格
- 下侧空间中,得到的数据客户映射到对应的格
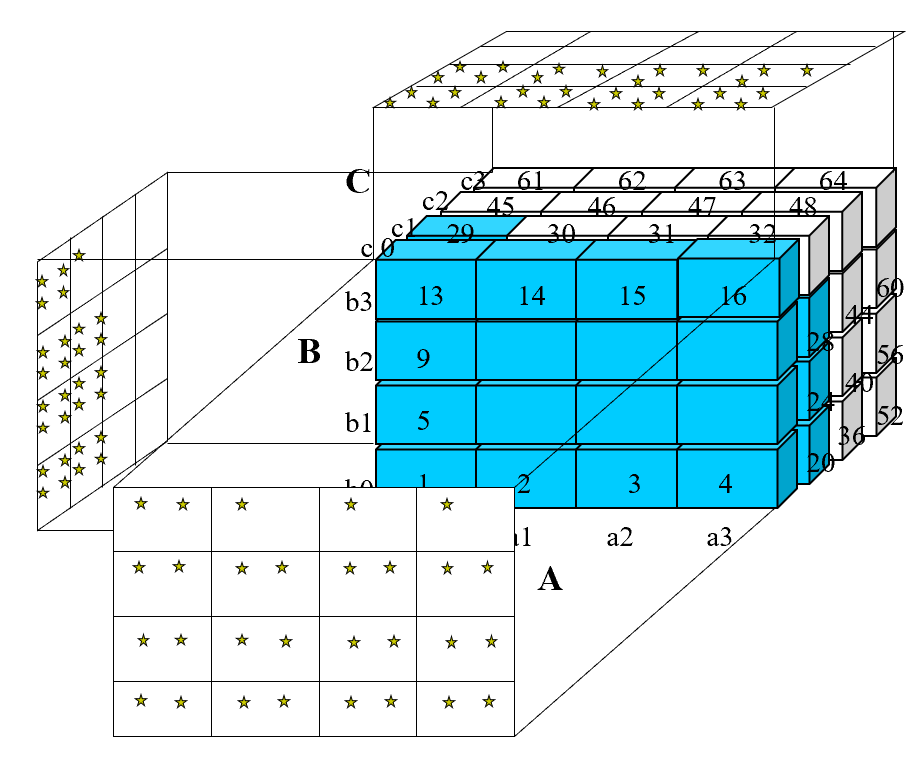
左侧空间中,已经存放了29个星
 |
 |
|---|
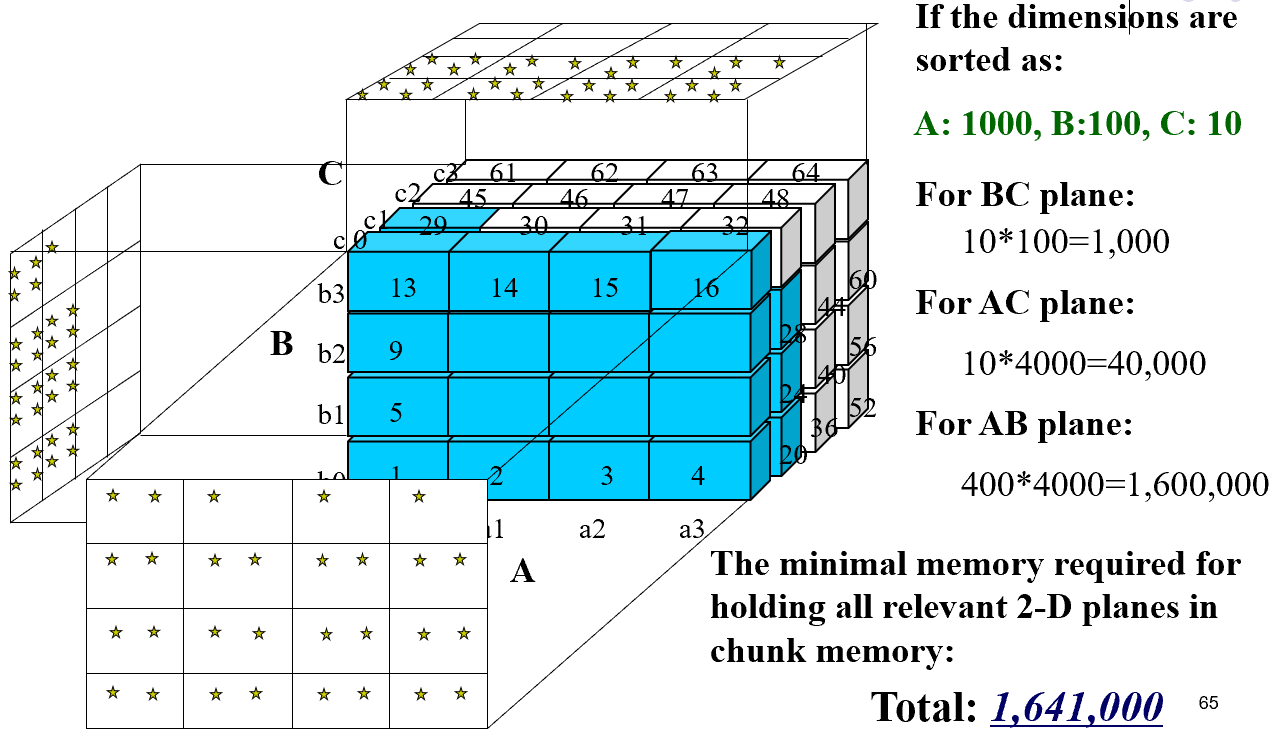
- 对比上面的两种情况,下者比上面的部分要大10倍
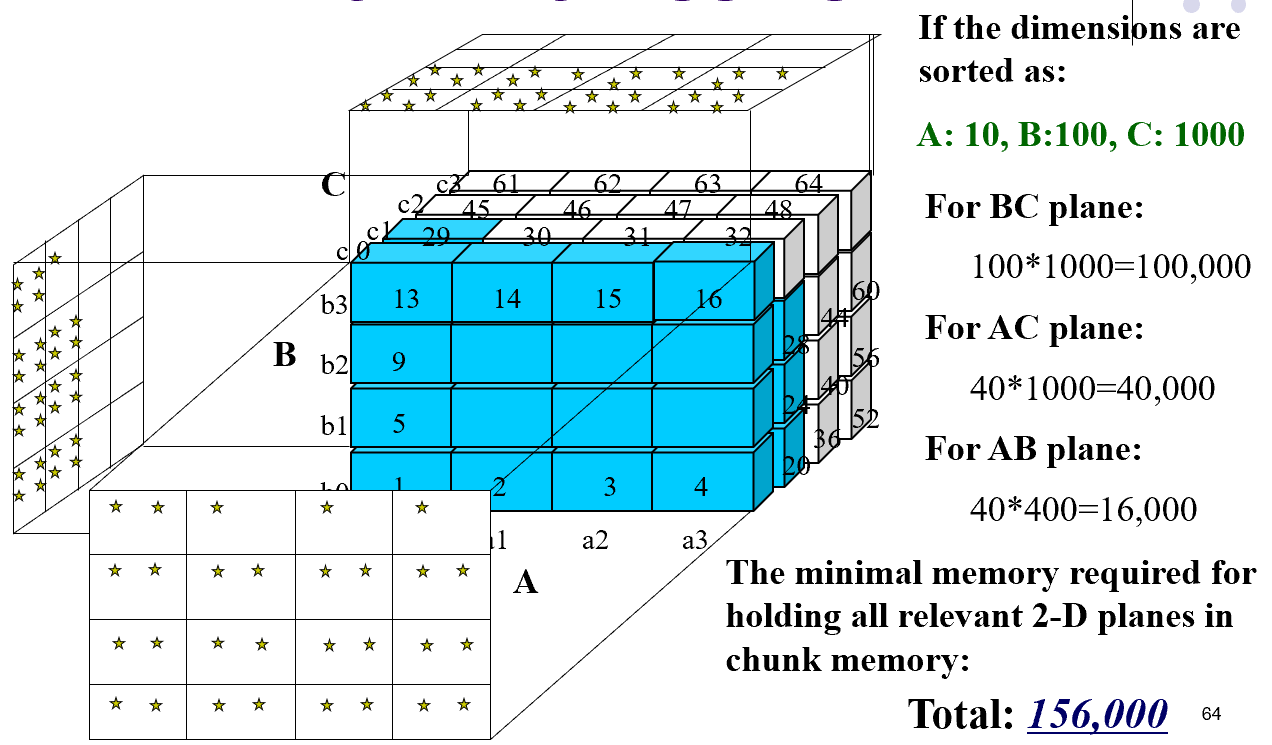
- 我们调用要按照维度从小到大的方式来调用,这样子可以保证所有的二维物化表空间最小化。
- A,B,C是该多维模型的维度,其中右边的数量是A,B,C三个维度上的"刻度"大小,即在图中的一小格,包含多少个可以区分的维成员。
- 因为物化的顺序不同的前提下,需要使用的中间存储空间分别是"一格","一列"和"一片"
6.7. OLAP与数据仓库
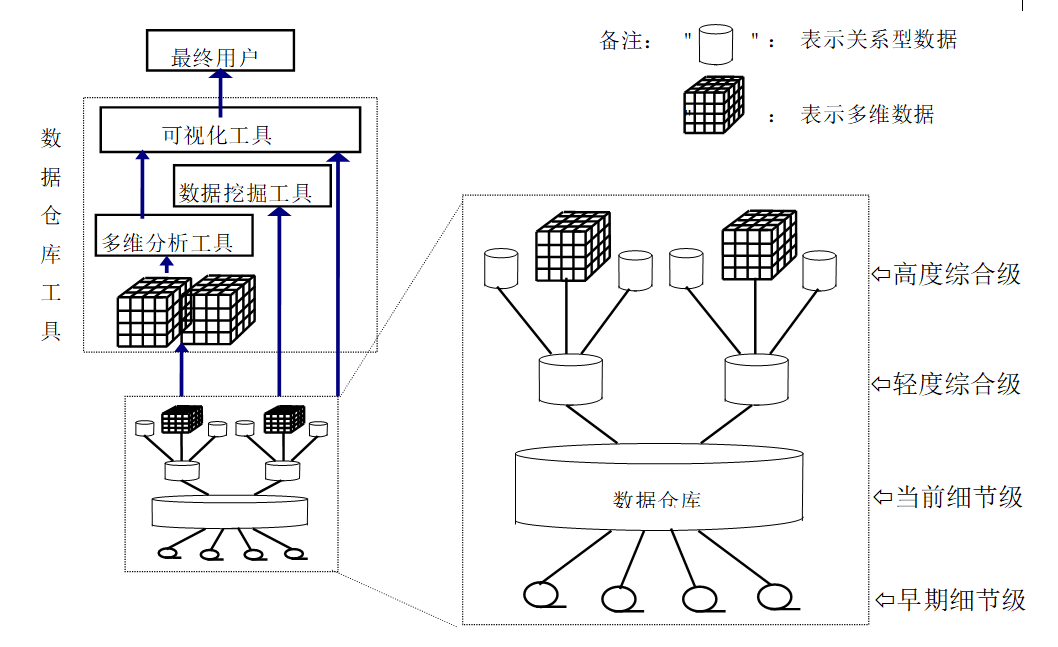
- 底层存储使用雪花模式完成存储
- 物化的部分,作为聚集层,作为在线的不同的物化视图
- 物化视图通过数据立方体来串联在一起
- 轻度综合级和高度综合级是没有严格的划分的
- 数据仓库中以主题为核心构建出来的不一定使用OLAP进行访问,被记录在数据仓库中元数据中和数据访问相关的部分。
- 数据仓库软件都是支持多种数据模型的
- 在OLAP服务器上可以存放部分私有资源(从数据仓库中拿到后计算得到的,但是只在OLAP中使用),OLAP中物化视图不一定都要放到数据仓库中,如果有共享的部分则放置到数据仓库,而如果不是则不必占用公共资源,之后不再关心这部分,因为对我们是透明的。
7. 多维数据分析
- 多维分析是指对以多维形式组织起来的数据采取切片、切块、旋转、钻取等各种分析动作,以求剖析数据,使最终用户能从多个角度、多个侧面地观察数据,从而深入地了解被包含在数据中的信息、内涵。
- 基本操作
- 切片(Slice):根据某一维上的某个维成员值选择统计数据进行分析
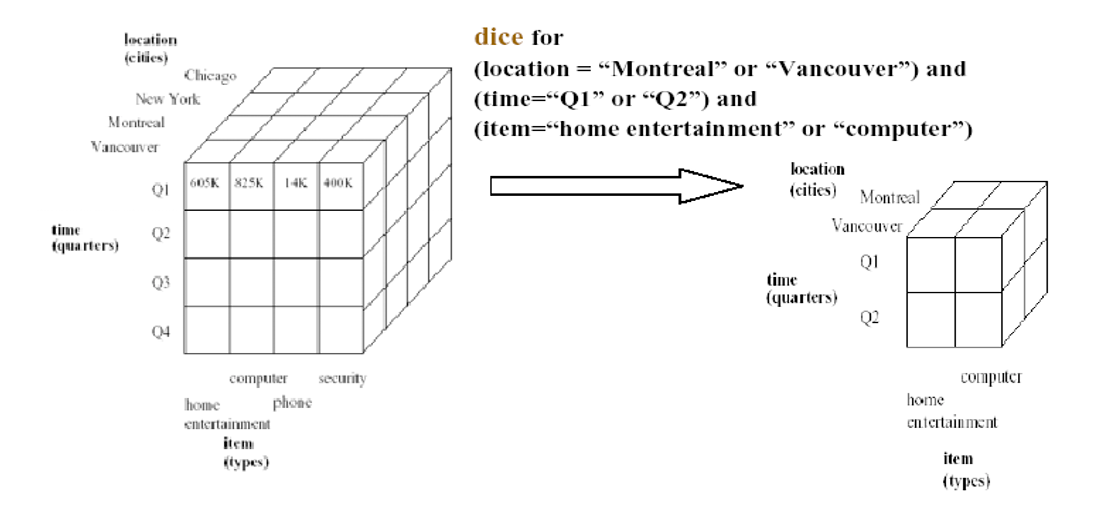
- 切块(Dice)
- 根据某一维上的某个维成员取值的区间选择统计数据进行分析
- 根据多个维度上的维成员取值的区间选择统计数据进行分析
- 旋转(Pivot/Rotate)调整维的排列次序的动作称为旋转
- 上钻/数据概括(roll_up)将多维下标的取值提升到较高的概念层次上,从而形成新的统计查询结果,并进行分析。
- 下钻/数据细化(drill_down)将多维下标的取值降低到较低的概念层次上,从而形成更细致的统计查询结果,并进行分析。
- 在大多数OLAP中,我们拿到数据的第一步骤一般我们首先选择降维(缩小分析域),也就是我们选择部分属性出来进行观察,直接影响最后的分析效果。

7.1. 切片

7.2. 切块
7.3. 旋转
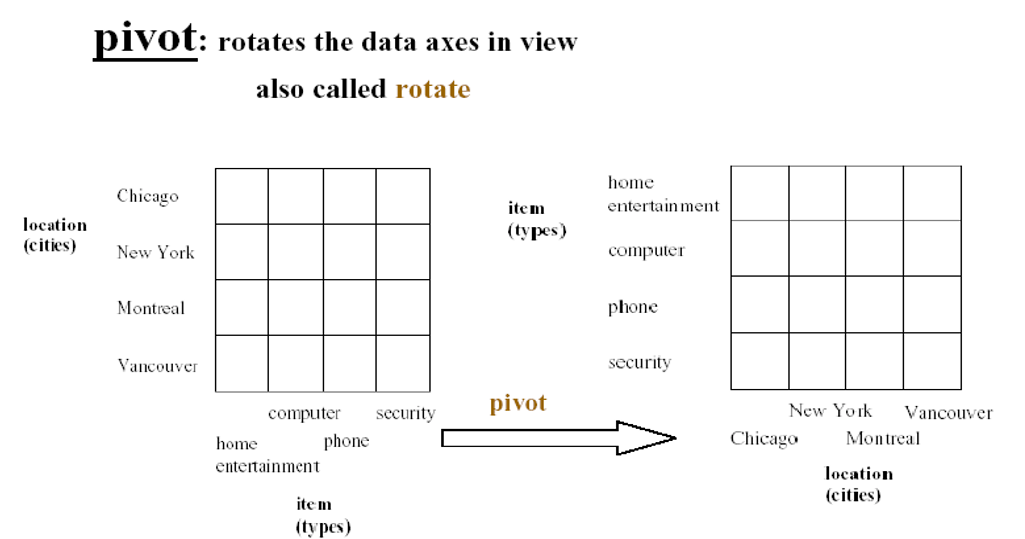
三维方体中有一个平面是被压缩在底下的,我们不好访问
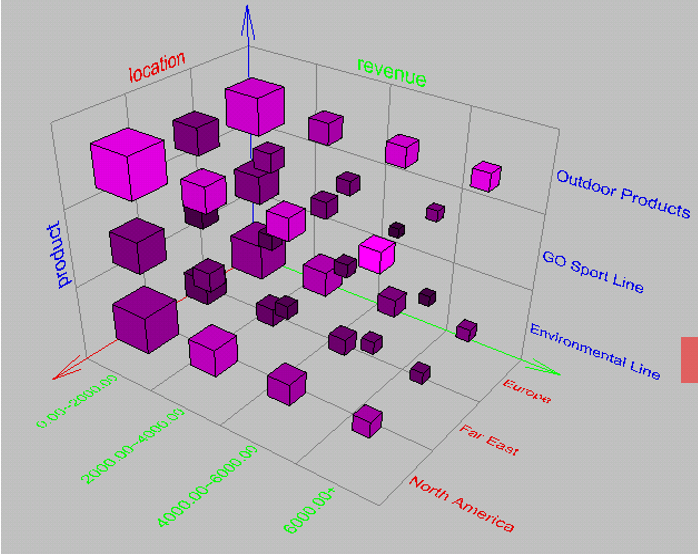
六维空间中,如果我们要交换红色轴和里面x轴是如何进行操作
7.4. 上钻
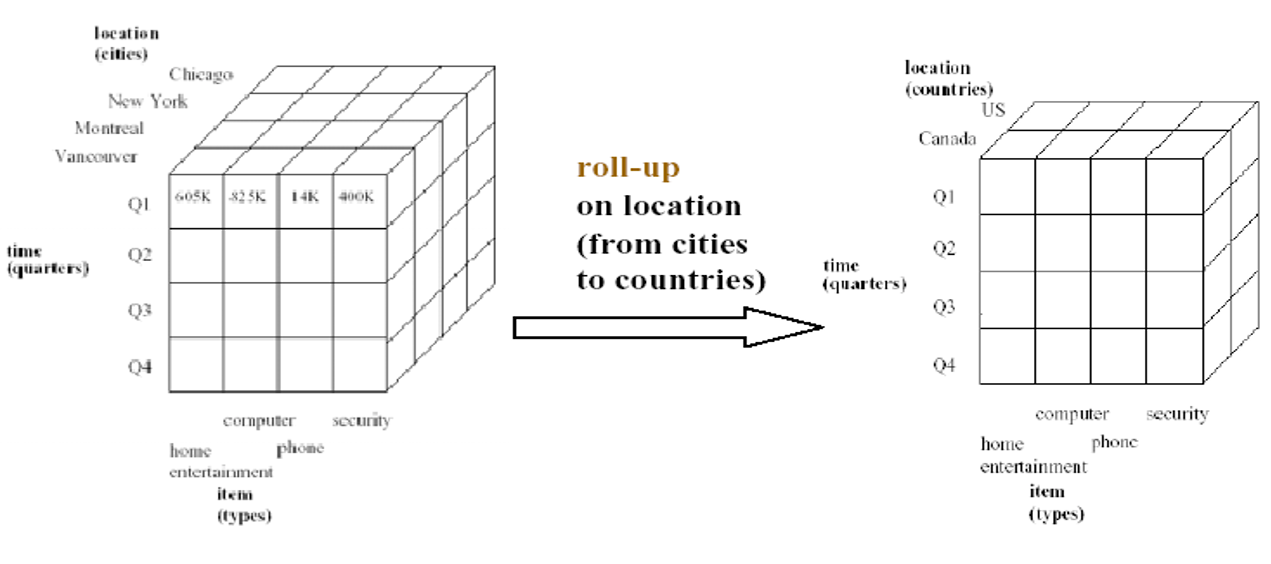
- 同一个维度同一层次的调整下,上钻和下钻是互为逆操作。
- 上钻:是将部分的数据进行压缩升高维度,将比较细的表达方式切换为比较粗的表达方式。
7.5. 下钻
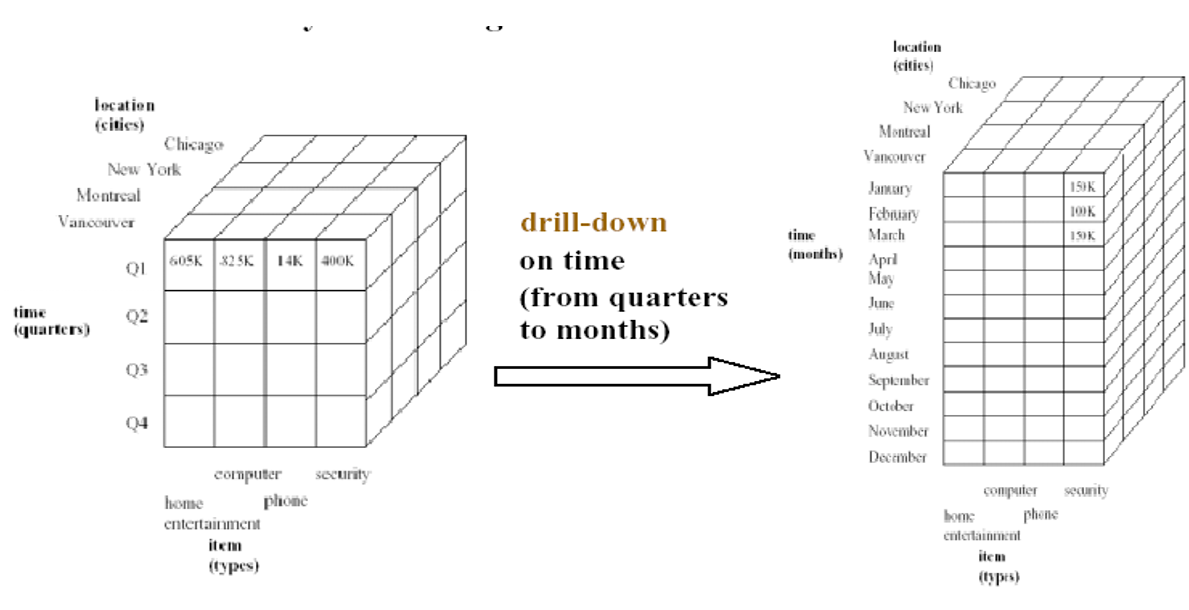
- 将比较粗的表达方式转换为比较细的表达方式
- 虽然我们目前只有两个维度的数据,但是数据是不足的,那么我们可能需要补充引入部分数据。
7.6. 其他操作
- 跨钻(drill across)对多个事实进行操作
- 钻透(drill through)下钻至数据立方体的最低细节后,继续细化至数据仓库/数据库的关系型表格
7.7. 发现驱动的探查
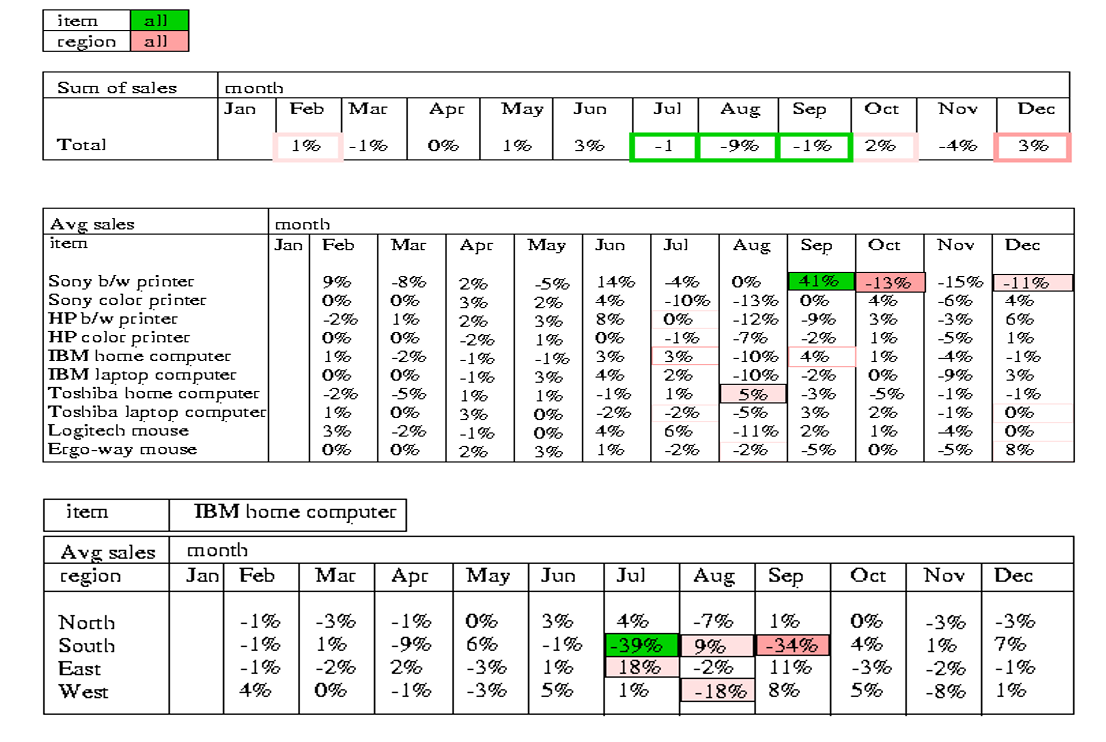
使用下钻和上钻等方式来对数据进行探查,对不同的部分中的异常部分进行下钻来溯源
2020-商务智能-Lecture3-OLAP
https://spricoder.github.io/2021/01/15/2020-Business-Intelligence/2020-Business-Intelligence-Lecture3-OLAP/