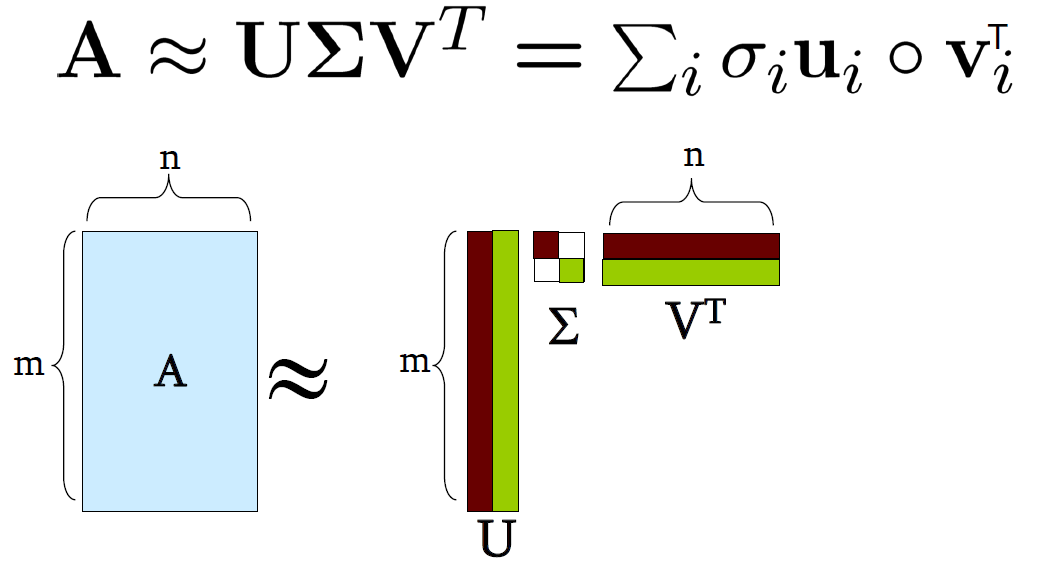2020-大数据分析-Lecture5-数据降维

Lecture5-数据降维

1. 降维(Dimensionality Reduction)

1. 我们假设数据能够在低维空间被表示
2. 高维数据在低维空间的表示是更加高效的。

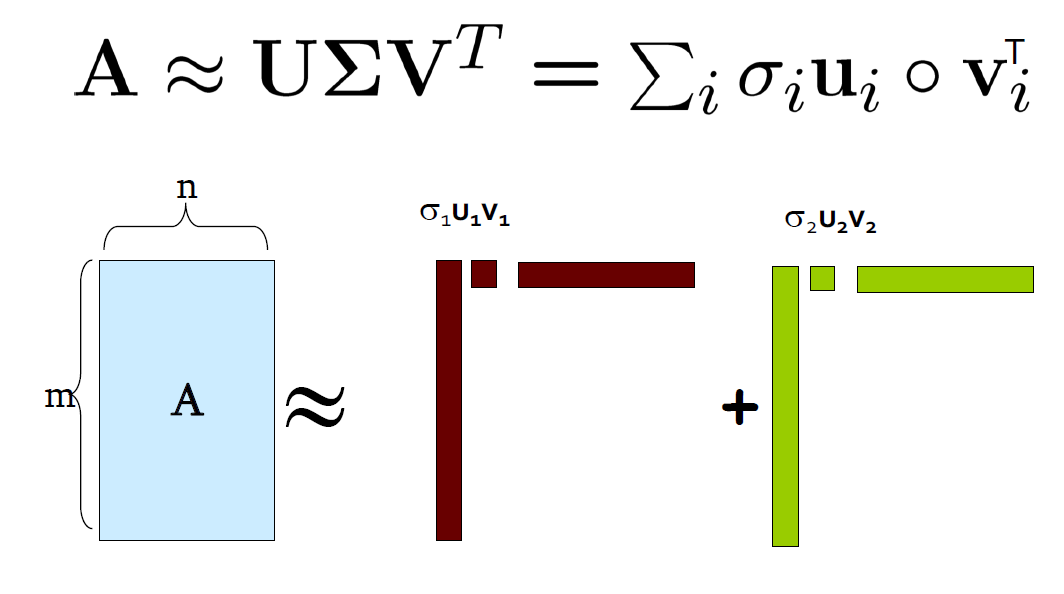
1.1. SVD示例

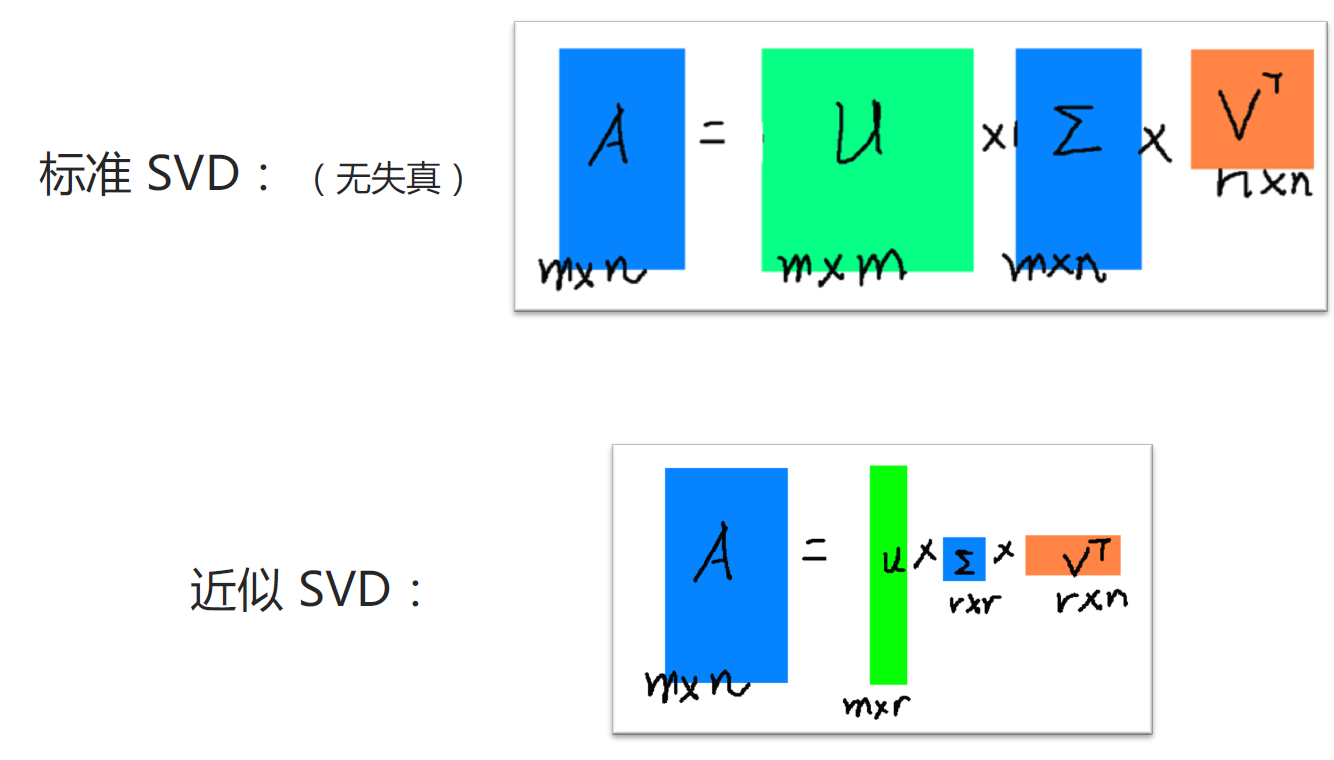
r表示保留的特征值的数量

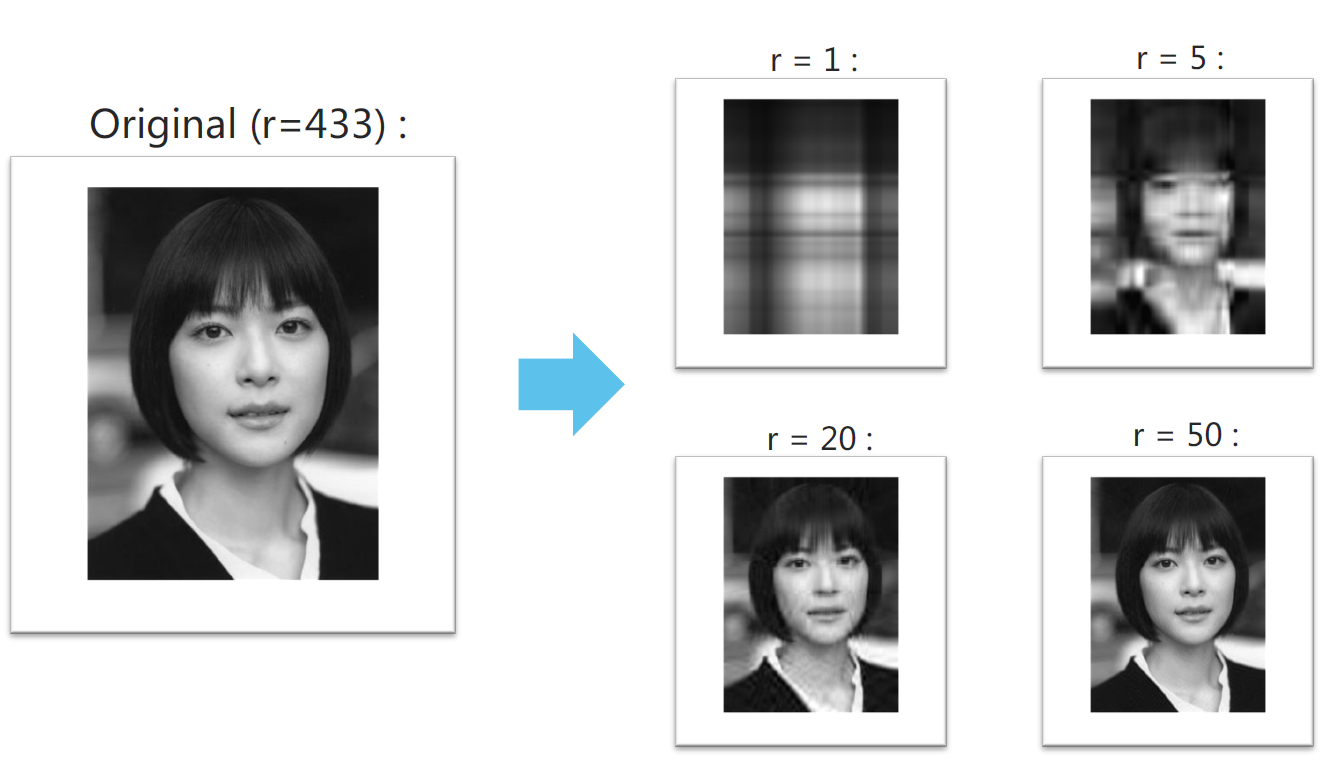
1.2. 压缩/降低尺寸

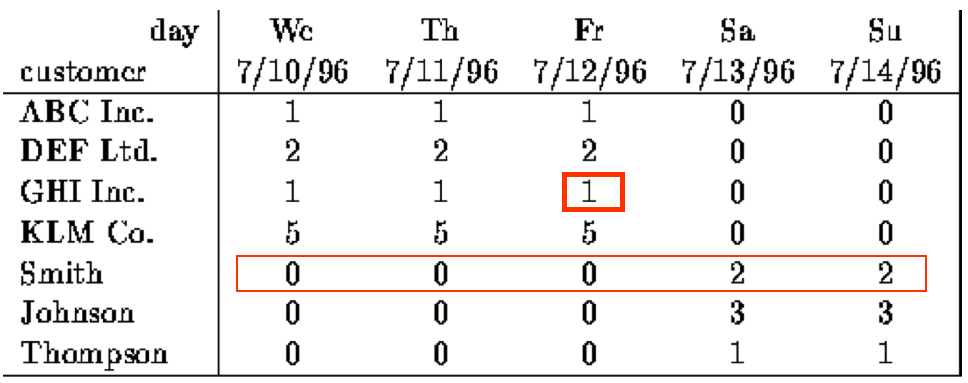
1. $10^6$行，$10^3$列，不更新
2. 随机访问一行数据，很少的错误时可以接受的
3. 如下的矩阵其实是个二维矩阵，我们通过缩放[1 1 1 0 0]或[0 0 0 1 1]可以重建所有的行

1.3. 矩阵的秩

1. 什么是矩阵A的秩?A的线性独立列数
2. 例子:

$A = \begin{bmatrix} 1 & 2 & 1 \\ -1 & -3 & 1 \\ 3 & 5 & 0 \\ \end{bmatrix}\ Rank(A) = 2$

1.4. 秩是可以降维

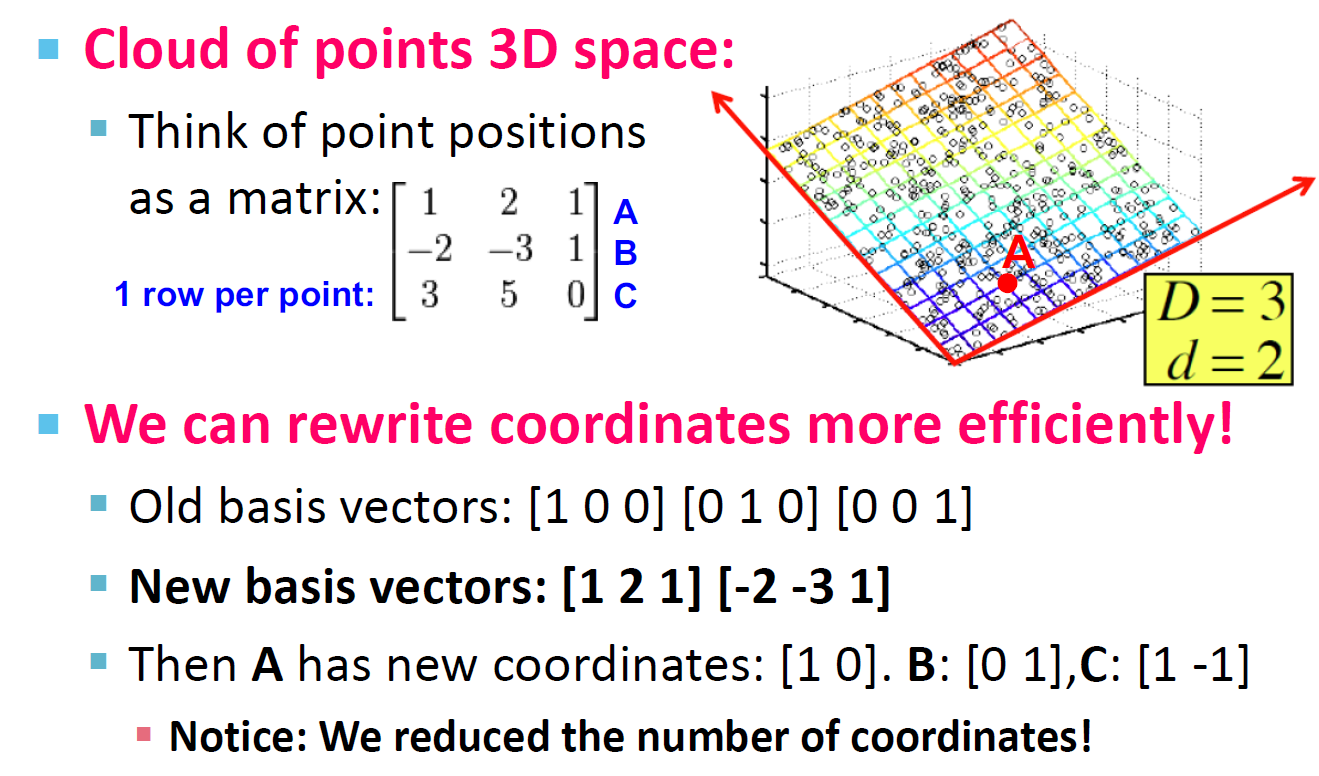
我们可以通过[1 2 1][-2 -3 1]两个向量来重写矩阵A，A的新坐标为:[1 0][0 1][1 -1]

1.5. 降维的目的

1. 数学上是发现数据中的轴
2. 发现隐藏的联系和主题:比如经常一同出现的单词等
3. 移除相似和噪声特征:并不是所有单词都是有用的
4. 数据解释和可视化
5. 更容易处理和存储数据：(找到规律，压缩数据量)

1.6. 降维的描述

1. 与用两个坐标表示每一个点不同，我们用轴上的坐标表示每一个点(对应红线上点的位置)。
2. 通过这样做，我们会产生一些错误，因为这些点并不完全在直线上(信息损失)，需要我们考虑我们是否可以接受这部分信息损失。

2. SVD

奇异值的值必然为正

2.1. SVD的分类

2.2. SVD的介绍

1. 变量(维数)较多，增加了分析问题的复杂性
2. 数据丰富但知识贫乏:实际问题中，变量之间可能存在一定的相关，因此，多变量中可能存在资讯的重叠
3. 人们自然希望通过克服相关、重叠性，用较少的变量来代替原来多的变量，而这种代替可以反映原来多个变量的大部分资讯，这实际上是一种"降维"的思想。

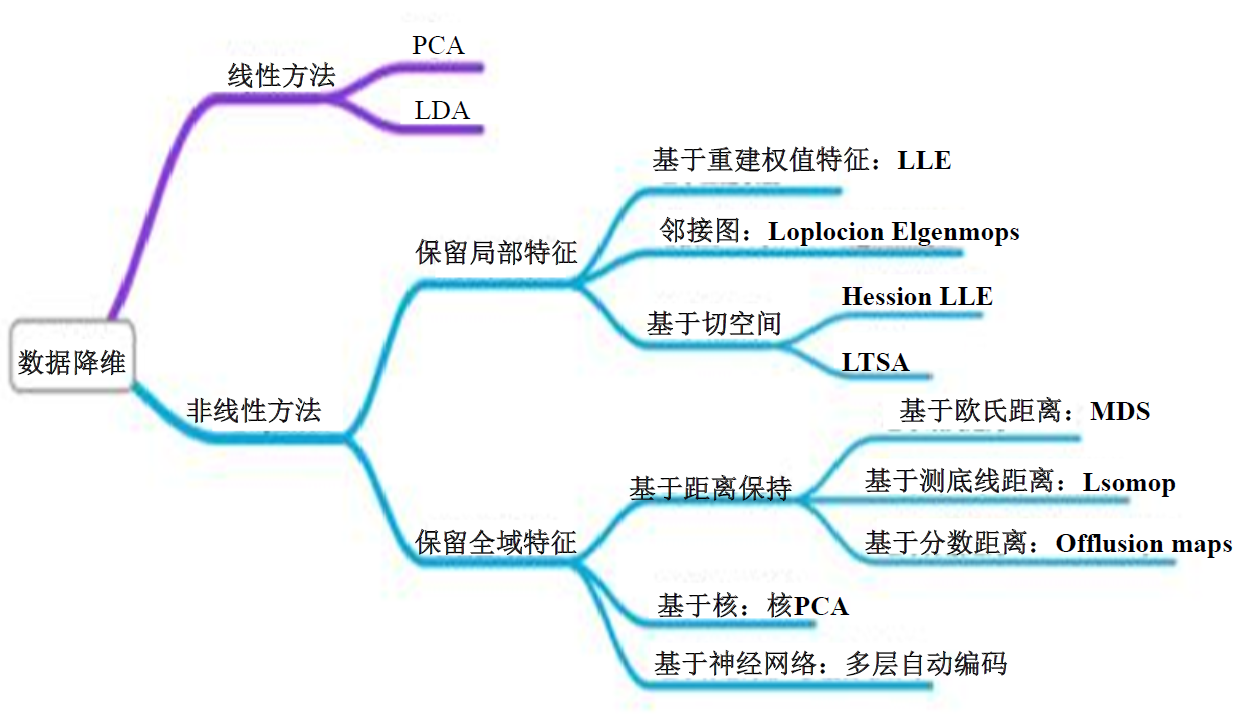
3. 降维方法汇总

3.1. 特征值与特征向量

1. 设$A$是$n$阶矩阵，如果数$\lambda$和n维非零列向量使关系式$Ax = \lambda x$成立
2. 则称$\lambda$是方阵A的特征值，非零向量x称为A的对应特征值的特征向量。
3. 一般求解方法

$|A - \lambda I| = 0 \iff \begin{vmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ . & . & ... & . \\ a_{n1} & a_{n2} & ... & a_{nn} \\ \end{vmatrix} = 0$

3.2. 降维方法

1. PCA(主成分分析，Principal-Component Analysis)
2. LDA(线性判别分析)
3. 因子分析
4. SVD(奇异值分解，Singular-Value Decomposition)
5. CUR分解

4. SVD(奇异值分解，Singular-Value Decomposition)

$A_{[m * n]} = U_{[m * r]} * \Sigma_{[r * r]} (V_{[n * r])^T}$

矩阵符号	矩阵名称	矩阵描述
$A$	输入数据矩阵	m * n维
$U$	左奇异矩阵	m * r维，正交矩阵，$UU^T = I$
$\Sigma$	奇异值对角矩阵	r * r维，r是矩阵A的秩，只有对角线上有值，其他元素均为0
$V$	右奇异矩阵	n * r维，正交矩阵，$V^TV = I$

Notes:奇异值分解的信息下降是非常快的，基本上前100个奇异值就可以表征大多数的数据。

4.1. SVD图示

4.2. 奇异值求解

$AA^T = U\Sigma V^TV\Sigma^TU^T = U\Sigma\Sigma^TU^T \tag{1-1}$

$A^TA = V\Sigma U^TU\Sigma V^T = V\Sigma^T\Sigma V^T \tag{1-2}$

我们通过简单分析可以知道$AA^T$和$A^TA$是对称矩阵

1. 我们利用上面的(1-1)式来进行特征值分解，得到的特征矩阵就是U
2. 通过上面的(1-2)式来进行特征值分解，得到的特征矩阵就是V
3. 对$\Sigma\Sigma^T$或者$\Sigma^T\Sigma$中的特征值开方，可以获得所有的奇异值

4.3. SVD计算示例

$A = \begin{bmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{bmatrix} \ A^T = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 1 & 0 \end{bmatrix}$

求解特征值要从大到小排列

矩阵名	矩阵值	特征值	特征矩阵
$U$	$U = A * A^T = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 1 & 1\end{bmatrix}$	$\lambda_1 = 3, u_1 = (\frac{1}{\sqrt{6}},\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}})^T$ $\lambda_2 = 1, u_2 = (\frac{1}{\sqrt{2}}, 0, -\frac{1}{\sqrt{2}})^T$ $\lambda_3 = 0, u_3 = (\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})^T$	$\begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{bmatrix}$
$V$	$V = A^T*A = (\begin{matrix} 2 & 1 \\ 1 & 2\end{matrix})$	$\lambda_1 = 3,v_1 = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) ^ T$ $\lambda_2 = 1,v_2 = (-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) ^ T$	$\begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix}$

求解奇异值为:$\sqrt{3}\ and\ 1$

4.4. SVD的性质

我们通常可以将一个实数矩阵A按照分解为$A = U\Sigma V^T$

1. $U,\Sigma,V$:唯一
2. U,V:列正交
   1. $U^TU = I,V^TV = I$，I是单位矩阵
   2. 列是正交单位向量
3. $\Sigma$:对角矩阵：对角值(奇异值)为正，并以降序排列

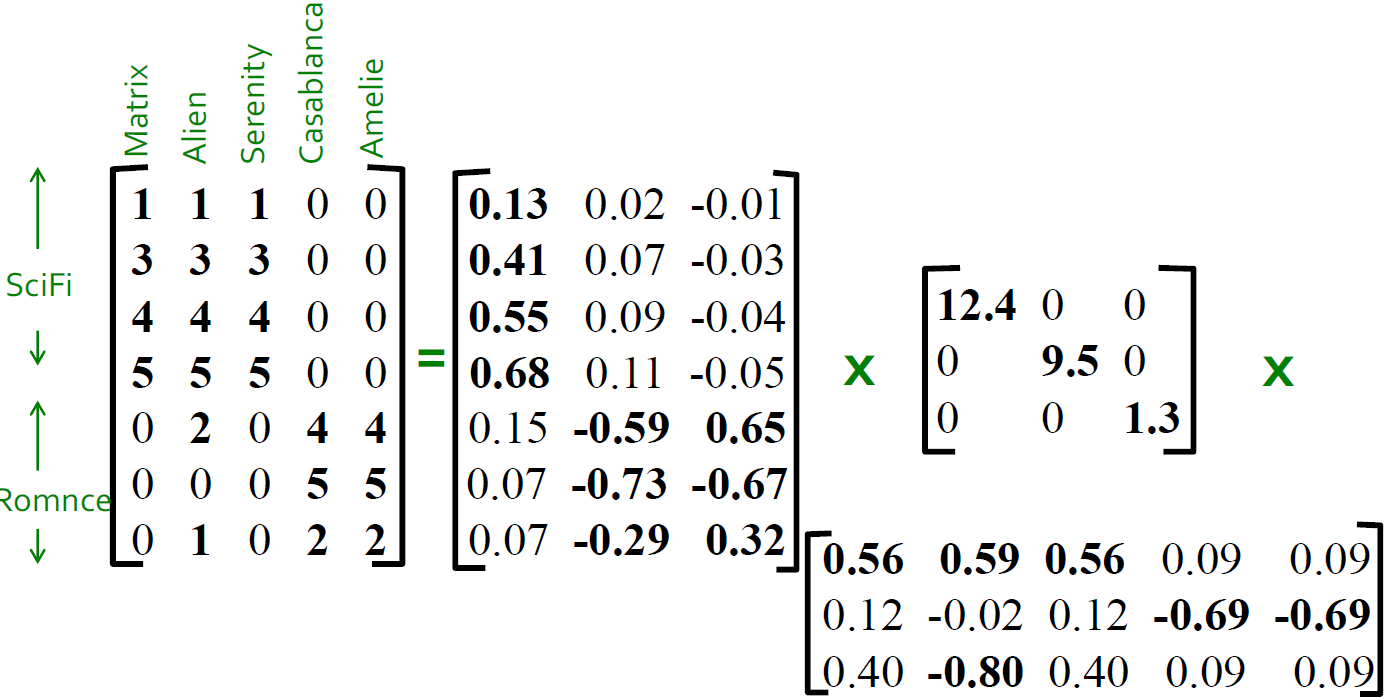
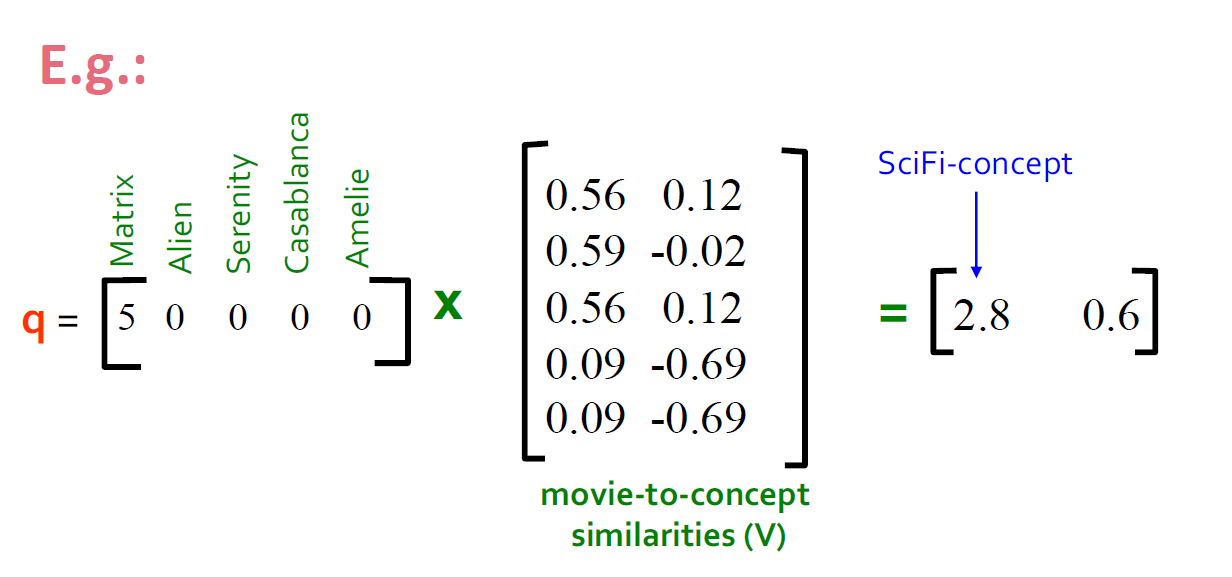
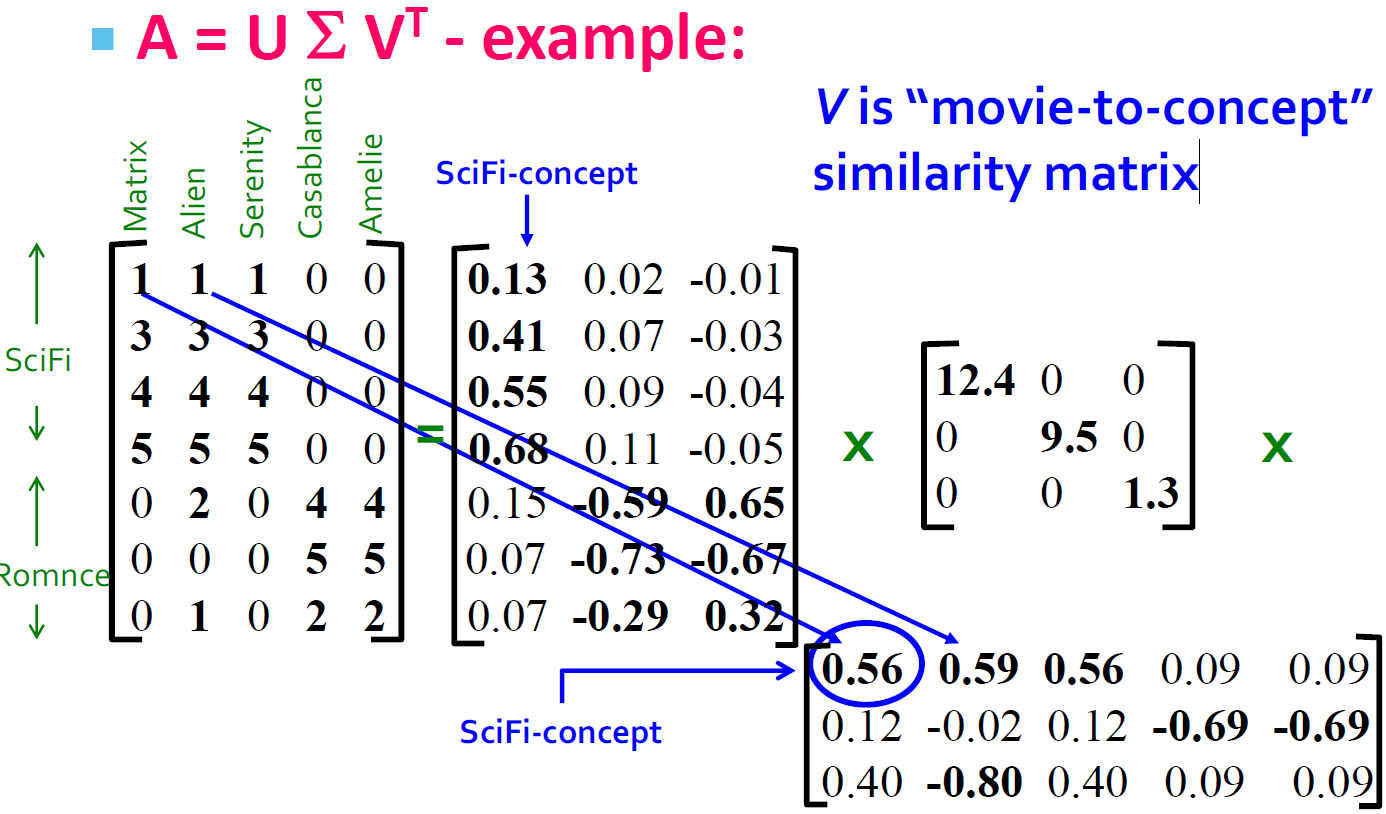
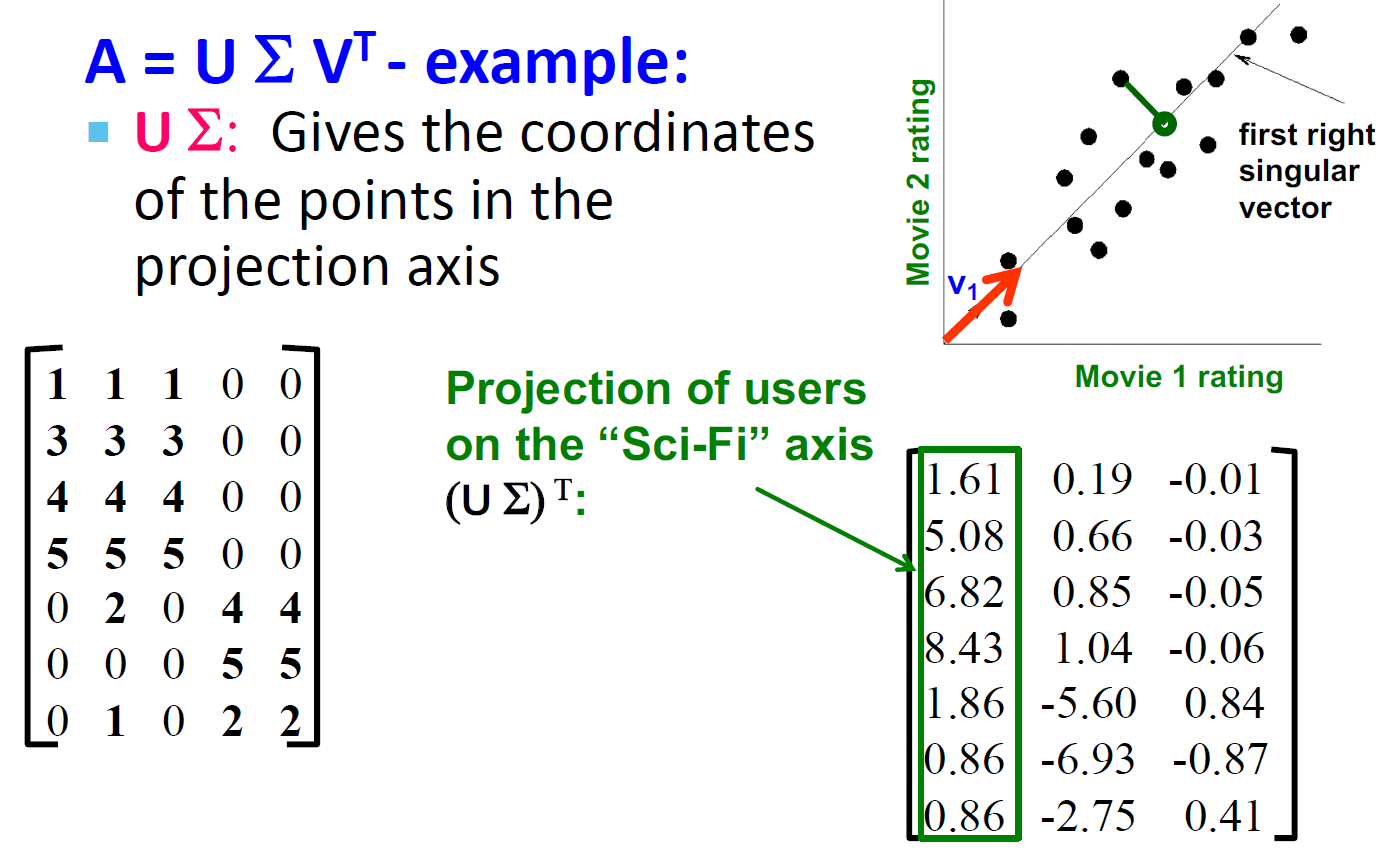
4.5. SVD的例子的解释(Users to Movies)

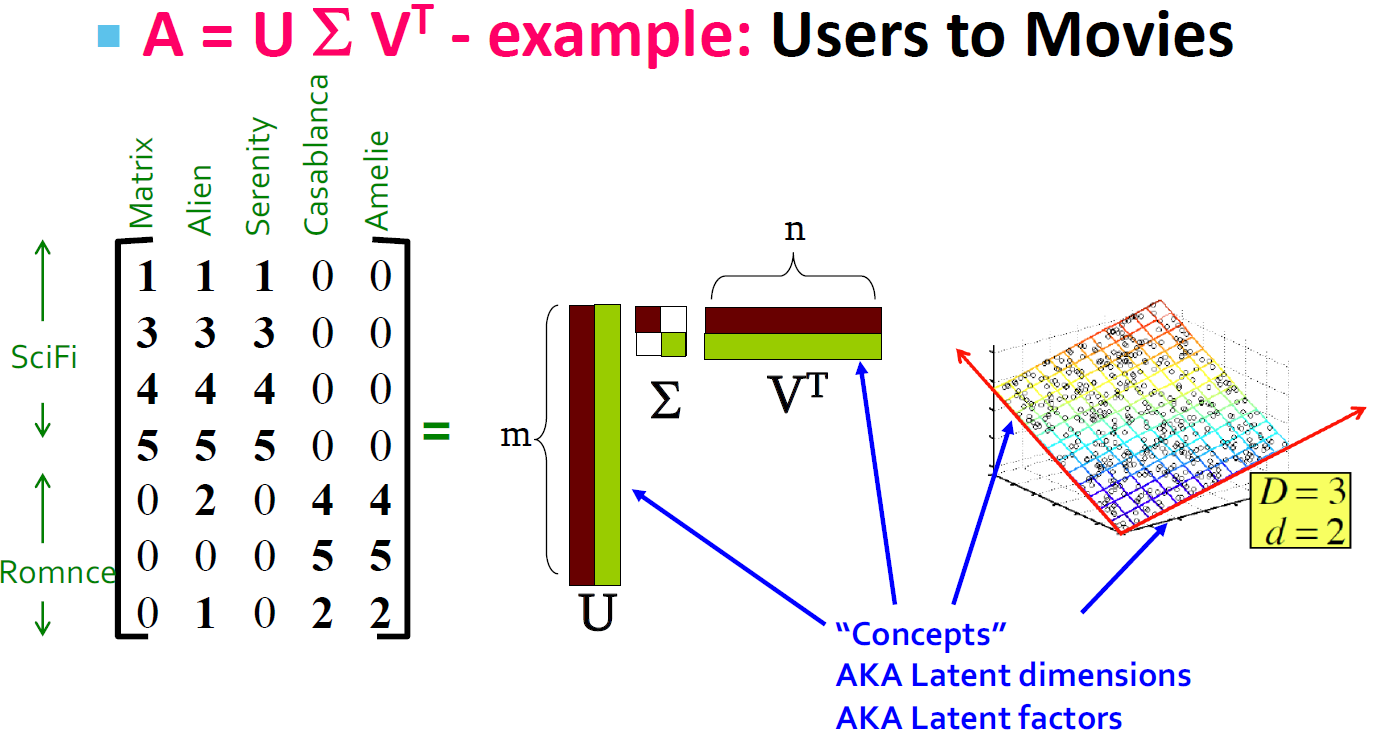
• U:"User to Concept"相似度矩阵
  • 第一列:SciFi-concept
  • 第二列:Romance-concept
• $\Sigma$:
  • 第一对角值:“strength” of the SciFi-concept
  • 对角值:“strength” of each concept
• V:"movie-to-concept"相似度矩阵

4.6. SVD的向量理解

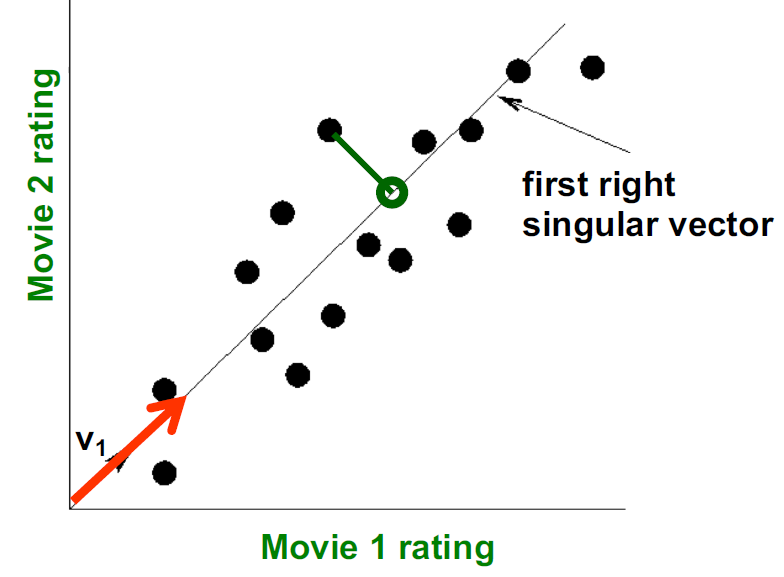
1. 不使用二维(x, y)来描述一个点,而是使用一个点z来描述这个点。
2. 点的位置是在向量v1上的
3. 如何选择v1:最小化reconstruction errors(我们选择使用欧氏距离)

4.6.1. 最小化 reconstruction errors

1. SVD目标:最小化 reconstruction errors

$\sum\limits_{i = 1}\limits^{N}\sum\limits_{j = 1}\limits^D||x_{ij} - z_{ij}||^2 \to 0$

2. 如何被认为是没有了，下降结束了？设置最小的奇异值为0

3. 得到SVD后的近似矩阵(将最小的奇异值设置为0和U、V中对应的行和列置为0，重新做乘法得到新的矩阵)

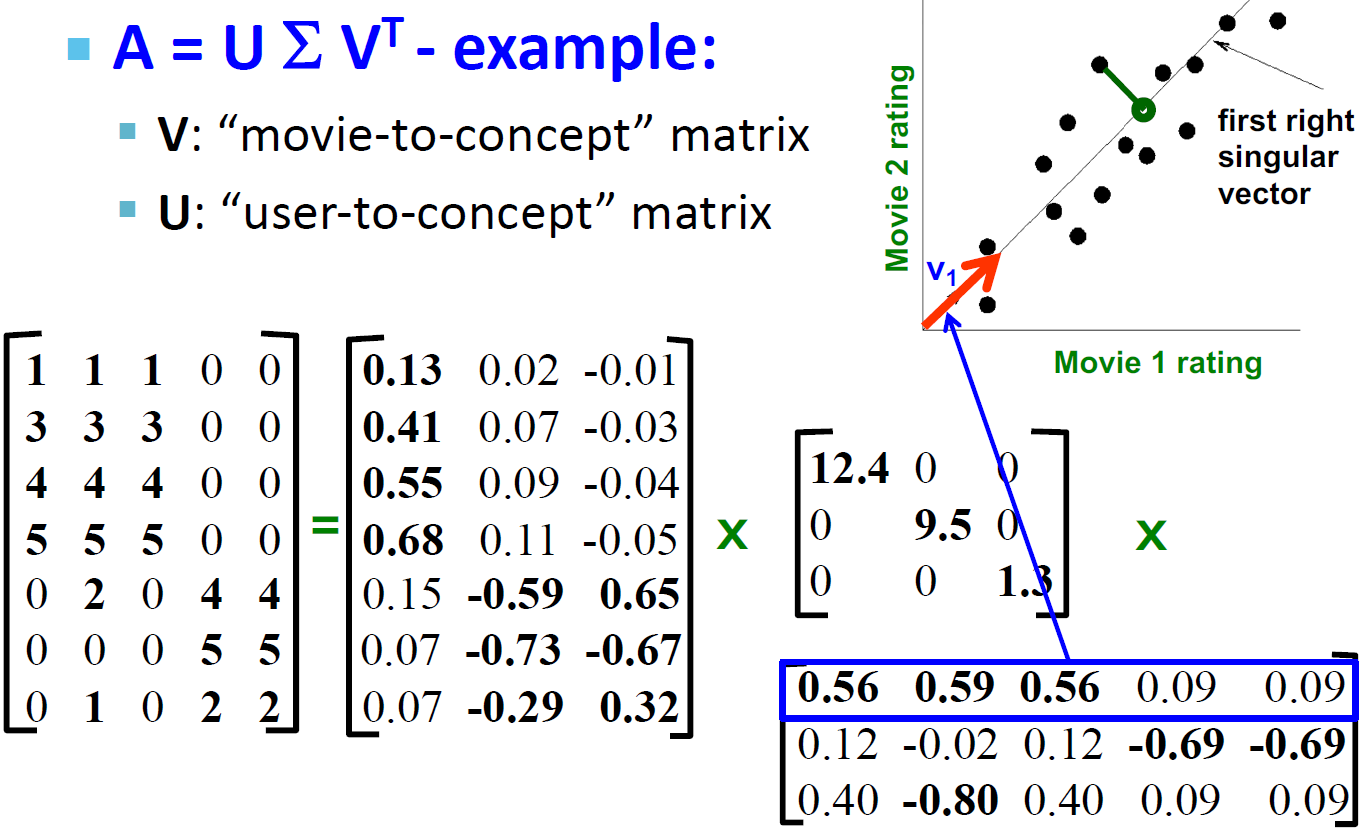
4.6.2. SVD向量理解例子:Users to Movies

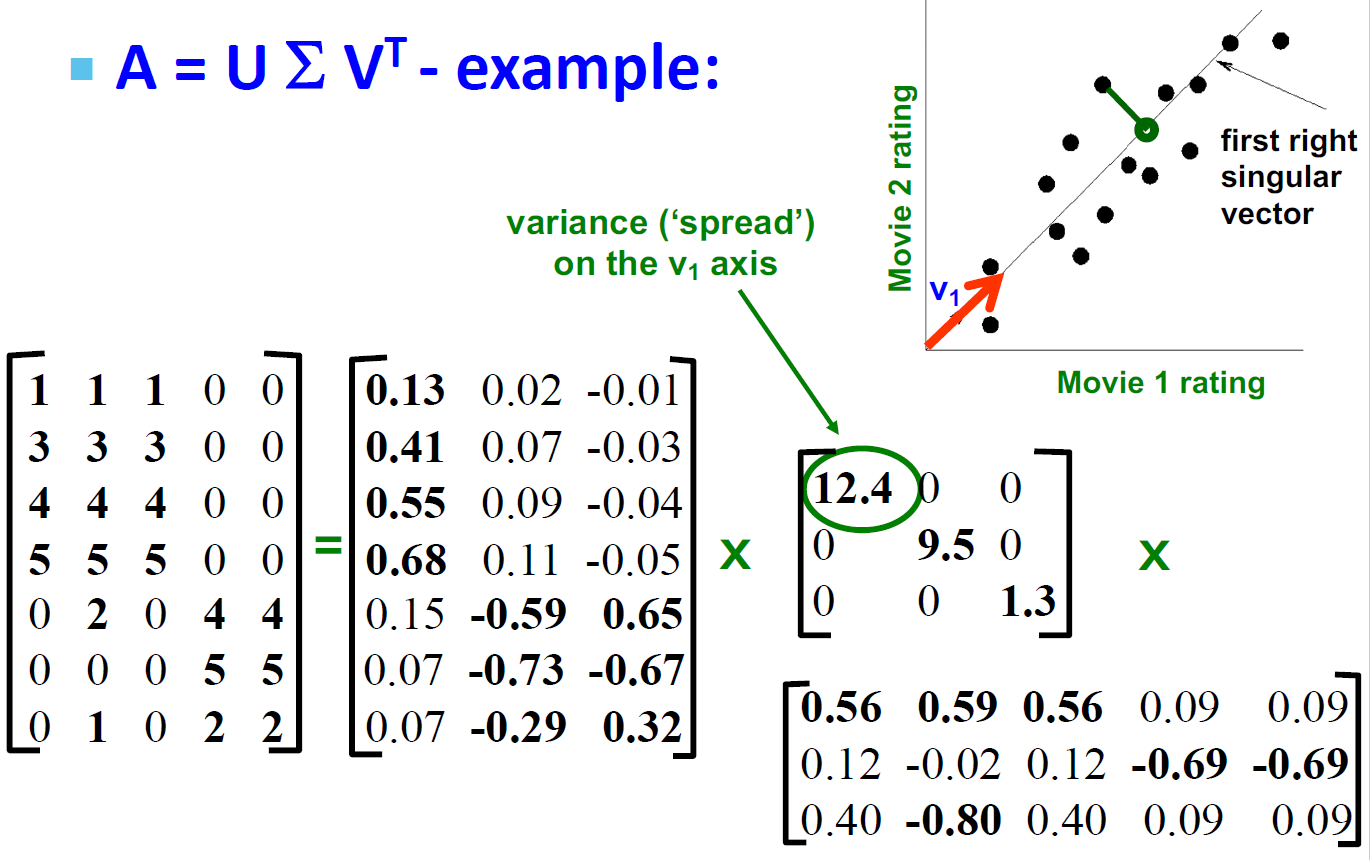
4.7. SVD - 最低秩近似

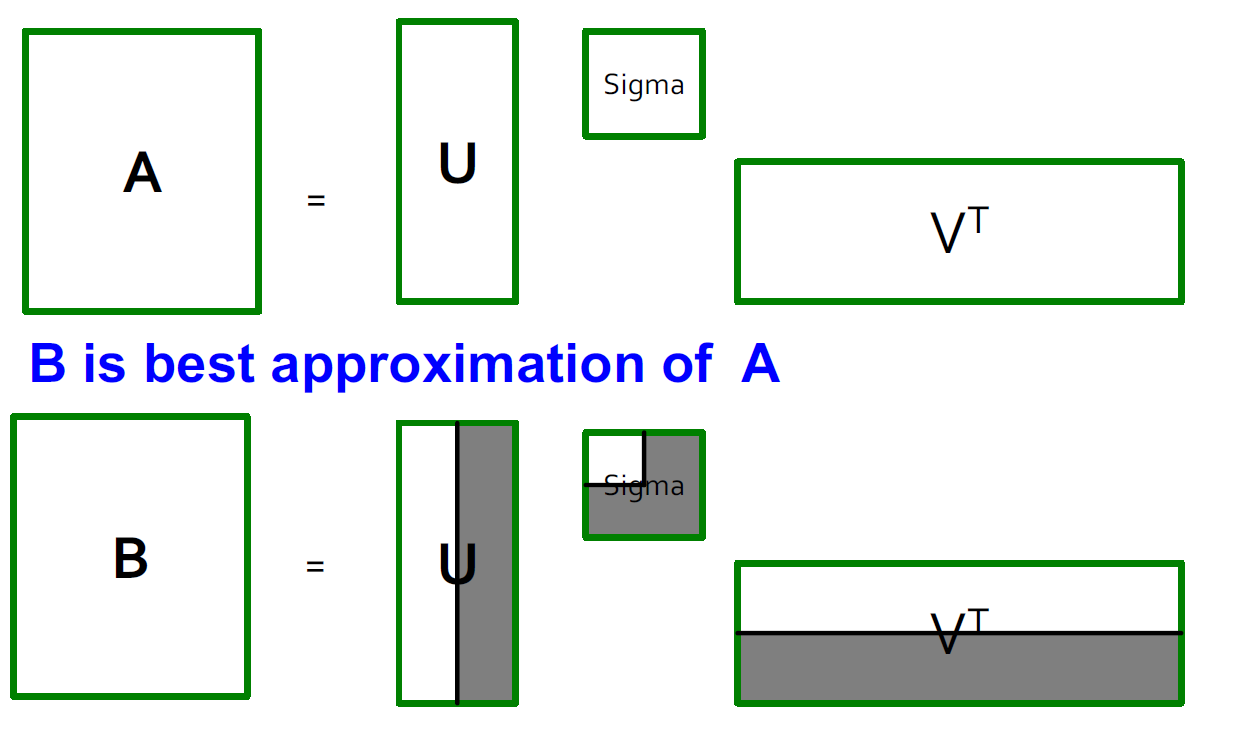
1. $定理:如果A = U\Sigma V^T并且B = U S V^T，并且S是一个对角r*r的矩阵，并且s_i = \delta_i(i = 1...k)，并且其他的s_i=0，那么B是A的最合适的近似矩阵，并且rank(B) = k$
2. 什么是最好?B在$rank(B) = k$的时候是$\min\limits_B||A-B||_F$的解
3. $||A-B||_F = \sqrt{\sum\limits_{ij}(A_{ij} - B_{ij})^2}$

4.7.1. 引理

1. $||M||_F = \sum\limits_i(q_{ii})^2$ 当 M = P Q R是M的SVD的时候
2. $U\Sigma V^T - USV^T = U(\Sigma - S)V^T$

4.7.2. 引理的证明

$\begin{array}{l} \|M\|=\sum\limits_i\sum\limits_j\left(m_{i j}\right)^{2}=\sum\limits_i \sum\limits_j\left(\sum\limits_k \sum\limits_lp_{i k} q_{kl} r_{lj}\right)^{2} \\ \|M\|=\sum\limits_i\sum\limits_j\sum\limits_k\sum\limits_l \sum\limits_n\sum\limits_m p_{ik} q_{kl} r_{lj} p_{in} q_{nm} r_{mj} \end{array}$

• $\sum\limits_ip_{ik}p_{in}$是1，如果k=n，不然为0
• P是列正交矩阵，R是正交矩阵，Q是对角矩阵

$\begin{array}{l} A = U \Sigma V^T, B = U S V^T \\ \\ \min\limits_{B, rank(B)=K}||A-B||_F \\ = \min ||\Sigma - S||_F = \min\limits_{s_i}\sum\limits_{i=1}\limits^r(\delta_i-s_i)^2 \end{array}$

• 我们想要的是最小化$\min\limits_{s_i}\sum\limits_{i=1}^r(\theta_i-s_i)^2$
• 解决方案就是令$s_i = \delta_i(i = 1...k)$并且其他$s_i=0$

$\begin{array}{l} \min\limits_{s_i}\sum\limits_{i=1}\limits^k(\delta_i-s_i)^2 + \sum\limits_{i = k + 1}\limits^r\delta^2 \\ = \sum\limits_{i = k + 1}\limits^r\delta^2 \end{array}$

4.7.3. 定理的说明

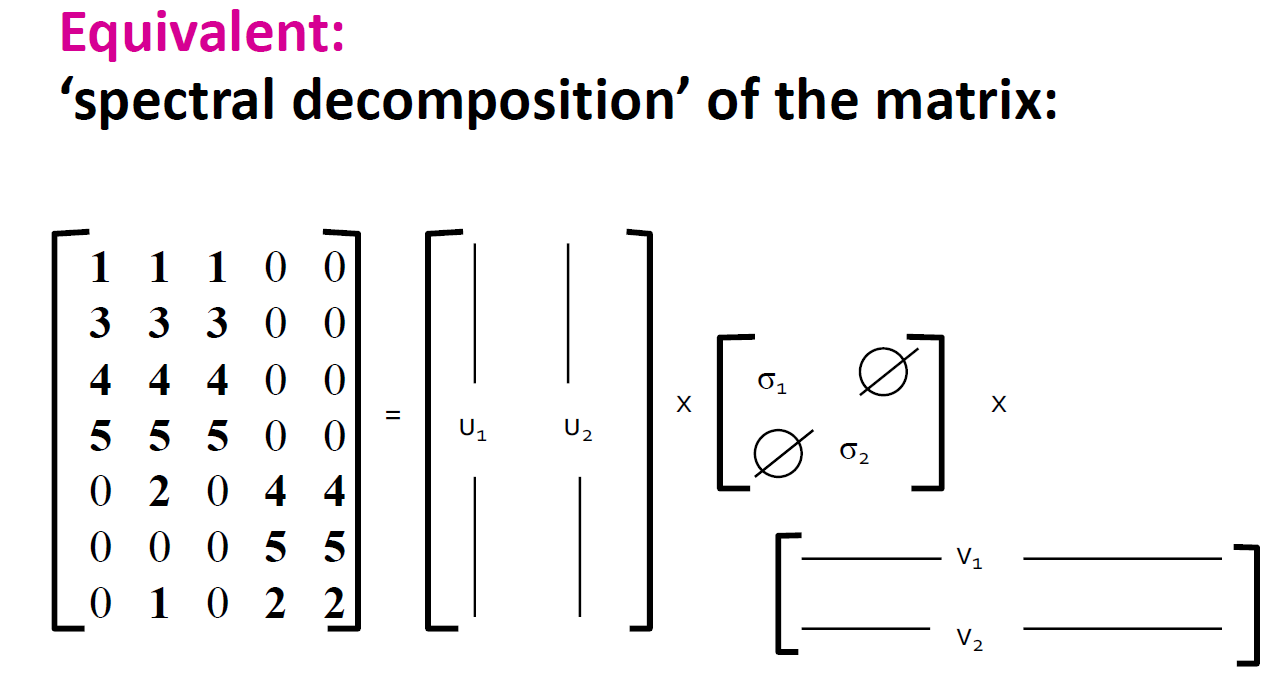
• 为什么将$\delta_i$设置为0是正确的做法？
  • 向量$u_i$和$v_i$是单位长度，所以$\delta_i$是用来调整他们的
  • 所以让$\delta_i$成为0可以导致更少的损失
• 我们应该保持多少$\delta_s$，拇指原则:$\sum\limits_i\delta_i^2$的和在80%-90%，保证信息损失不太多

4.8. SVD算法的复杂度

1. 计算SVD的复杂度:$min(O(nm^2), O(n^2m))$
2. 但是如果我们只想知道奇异值或者前k个奇异值，或者矩阵是稀疏矩阵，那么复杂度会大大下降

4.9. SVD和特征分解的关系

1. SVD角度：$A = U \Sigma V^T$

2. 特征分解的角度：$A = X \Lambda X^T$

   1. A是对称的
   2. U,V,X都是正交矩阵
   3. $\Lambda,\Sigma$都是对角的

$\begin{array}{l} AA^T \\ = U\Sigma V^T (U\Sigma V^T)^T \\ = U\Sigma V^T (V\Sigma^TU^T) \\ = U\Sigma\Sigma^TU^T(X \Lambda^2 X^T )\\ \\ A^TA \\ = V(\Sigma^TU^T)(U\Sigma V^T) \\ = V\Sigma\Sigma^TV^T(X \Lambda^2 X^T ) \end{array}$

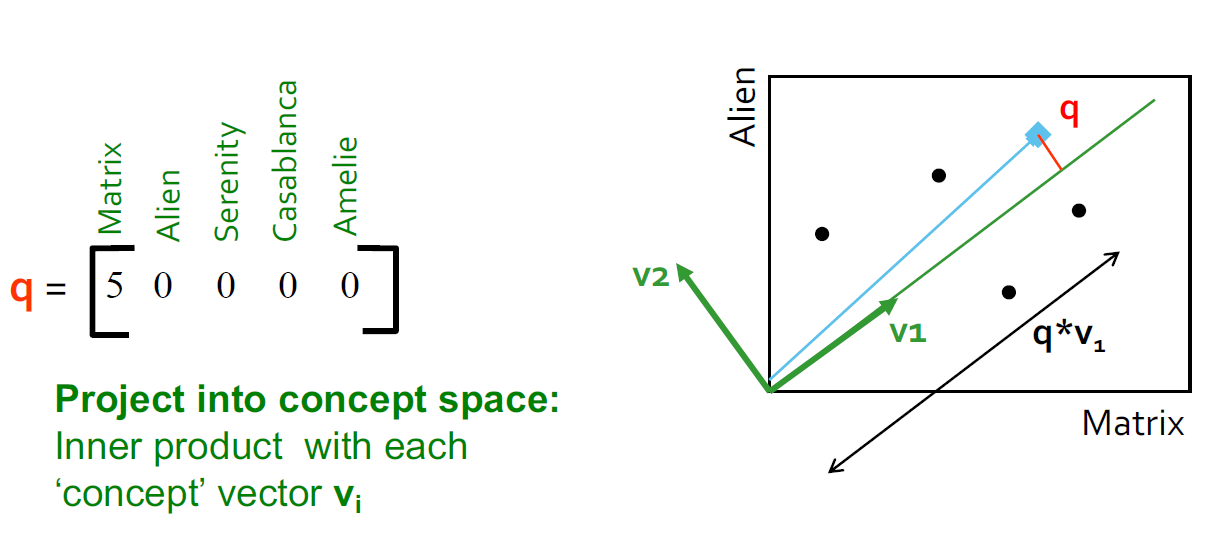
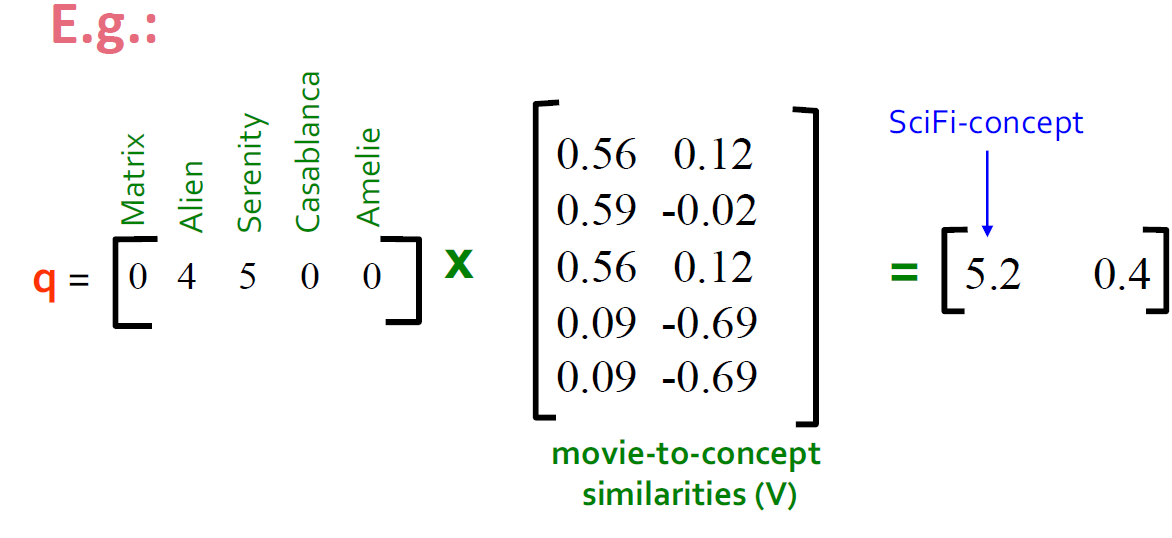
4.10. 案例:如何查询

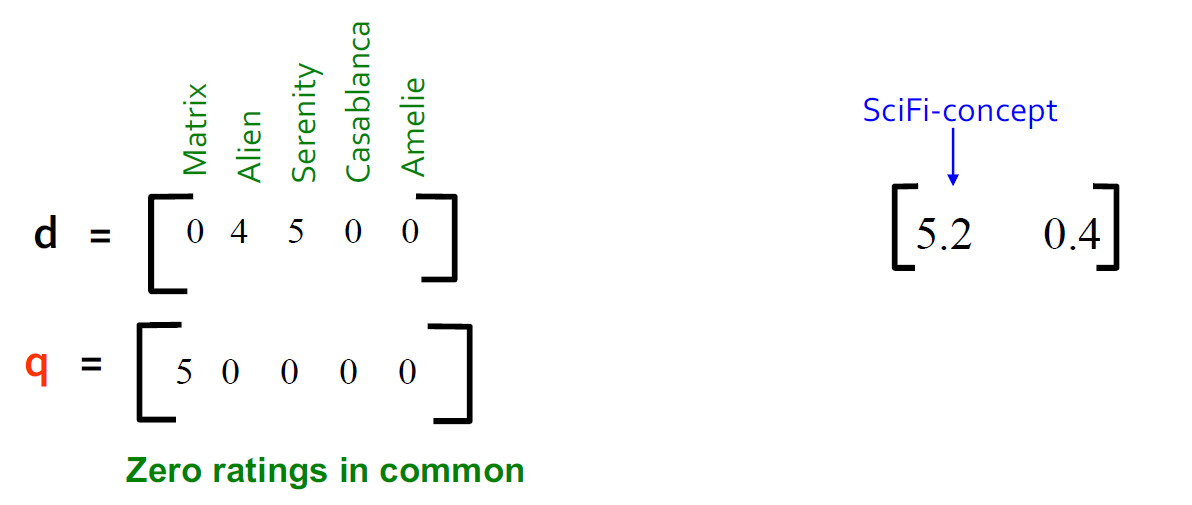
1. 查找类似这个矩阵的用户:将查询映射到"概念空间"中-怎么做？

1. user q:$q_{concept} = q V$
2. user d:$d_{concept} = d V$

1. 观察：被评级为"Alien"，" Serenity"的用户d与被评级为"Matrix"的用户q相似，尽管d和q的共同点为零！

4.11. SVD的效果

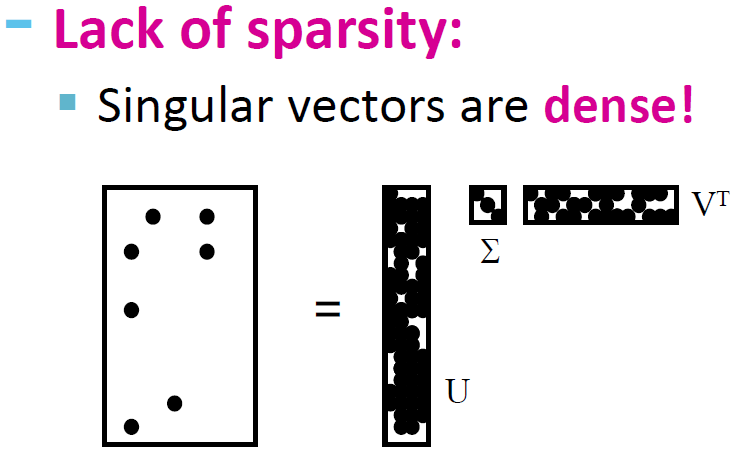
5. CUR分解

1. 目标:将矩阵A解释为C，U，R，使得$||A - C*U*R||_F$最小

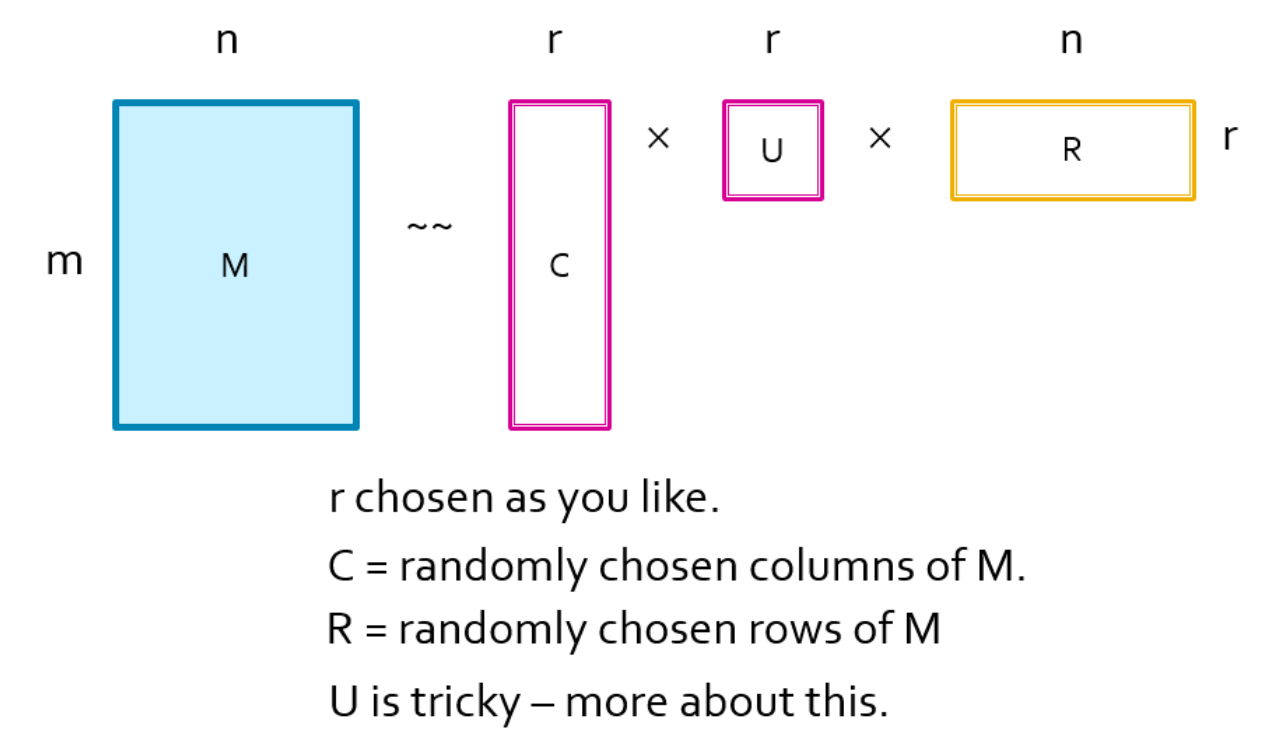
5.1. 选择行和列的方式

1. 尽管我们是随机的选择行和列，但是我们还是保留了对于重要的行和列的权重
2. 行和列的权重计算:$f=\sum\limits_{i,j}a_{ij}^2$
3. 我们按照概率$p_i = \sum\limits_{j}\frac{a_{ij}^2}{f}$选择行
4. 我们按照概率$q_j = \sum\limits_{i}\frac{a_{ij}^2}{f}$
5. 归一化处理:将所有的元素都是除以$\sqrt{rq_j}$(行)、$\sqrt{rp_i}$(列)

5.2. CUR对列(行)进行取样

1. 以列为例，行也是相似的
2. 输入:矩阵$A \in R^{m * n}$，样例数c
3. 输出:$C_d \in R^{m * c}$
4. 算法过程:
   1. 对于$\forall x \in [1, n]，P(x) = \frac{\sum\limits_iA(i, x)^2}{\sum\limits_{i,j}A(i,j)^2}$
   2. 对于$\forall i \in [1, c]$，以一列为例
      1. 选择$k \in [1, n]$满足分布P(x)
      2. 计算$C_d(:,i) = \frac{A(:,k)}{\sqrt{cP(k)}} = \frac{A(:, k)}{\sqrt{c * \frac{\sum\limits_iA(i, k)^2}{\sum\limits_{i,j}A(i,j)^2}}}$
5. 请注意，这是一种随机算法，同一列可以多次采样

5.3. 计算U

1. U是一个$r*r$的矩阵，所以是比较小的，并且如果他是高密度、难计算的也是可以的。
2. 首先计算W，我们让W是列C和行R的交集，并且计算出W的SVD表示为$W = X \Sigma Y^T$
3. 然后计算$\Sigma$的Moore-Penorse inverse(伪逆矩阵):$\Sigma$
   1. $\Sigma$是一个对角矩阵
   2. 他的Moore-Penorse inverse满足
      1. $\frac{1}{\sigma}$ 如果$\sigma \neq 0$
      2. 0 如果$\sigma=0$
4. 然后:$U = W^+ = Y(\Sigma^+)^2X^T$
   1. 非零奇异值的倒数：$\Sigma_{ii}^{+} = 1/\Sigma_{ii}$
   2. $W^+$是伪逆

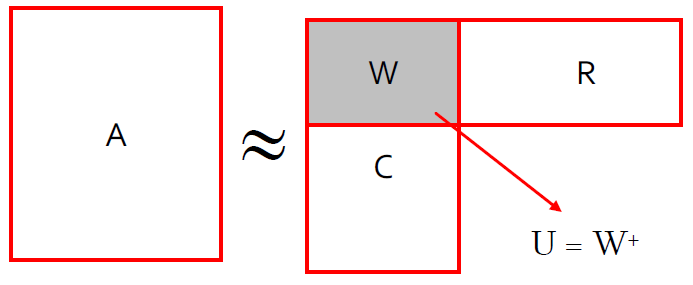
5.3.1. 为什么伪逆是有效的

$\begin{matrix} W = X \Sigma Y \\ W^{-1} = X^{-1} * \Sigma^{-1} * Y^{-1} \\ \because X^{-1} = X^T, Y^{-1} = Y^T \\ \Sigma^{-1} = \frac{1}{\Sigma_{ii}} \\ \end{matrix}$

• X、Y正交矩阵，$\Sigma$是对角矩阵
• 因此，如果W是非奇异矩阵，伪逆矩阵是真的逆矩阵

5.4. CUR是可以被证明是SVD的一个很好近似

5.5. CUR的优点和缺点

5.5.1. 优点

1. 很好计算：由于基向量是实际的列和行
2. 稀疏矩阵：由于基向量是实际的列和行

5.5.2. 缺点

1. 重复的列和行：大量的列将被多次采样

5.6. 如何避免重复

1. 方案一:直接抛弃
2. 方法二:用重复项的平方根缩放(乘)列/行

6. SVD和CUR

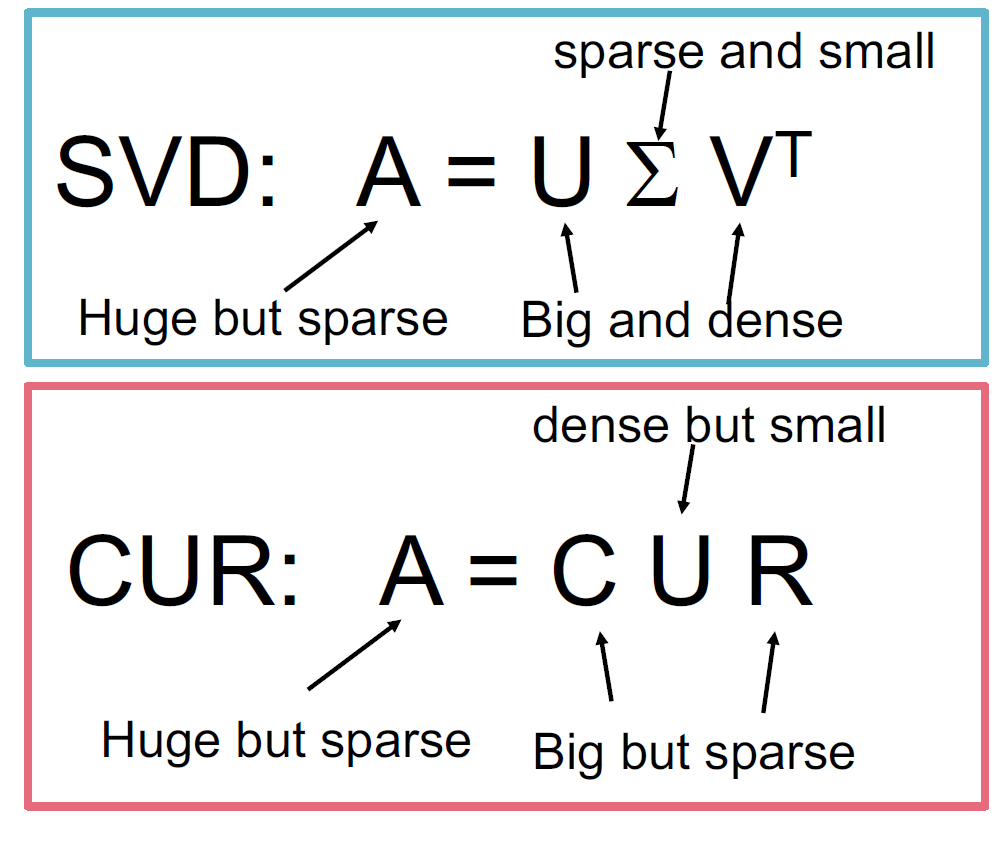
6.1. 简单的实验

1. DBLP bibliographic data
   1. Author-to-conference 的大稀疏矩阵
   2. $A_{ij}$:作者i在会议j上发表的论文数量
   3. 428k个作者(列)，3659会议(行)
   4. 非常稀疏

6.2. DBLP的结果

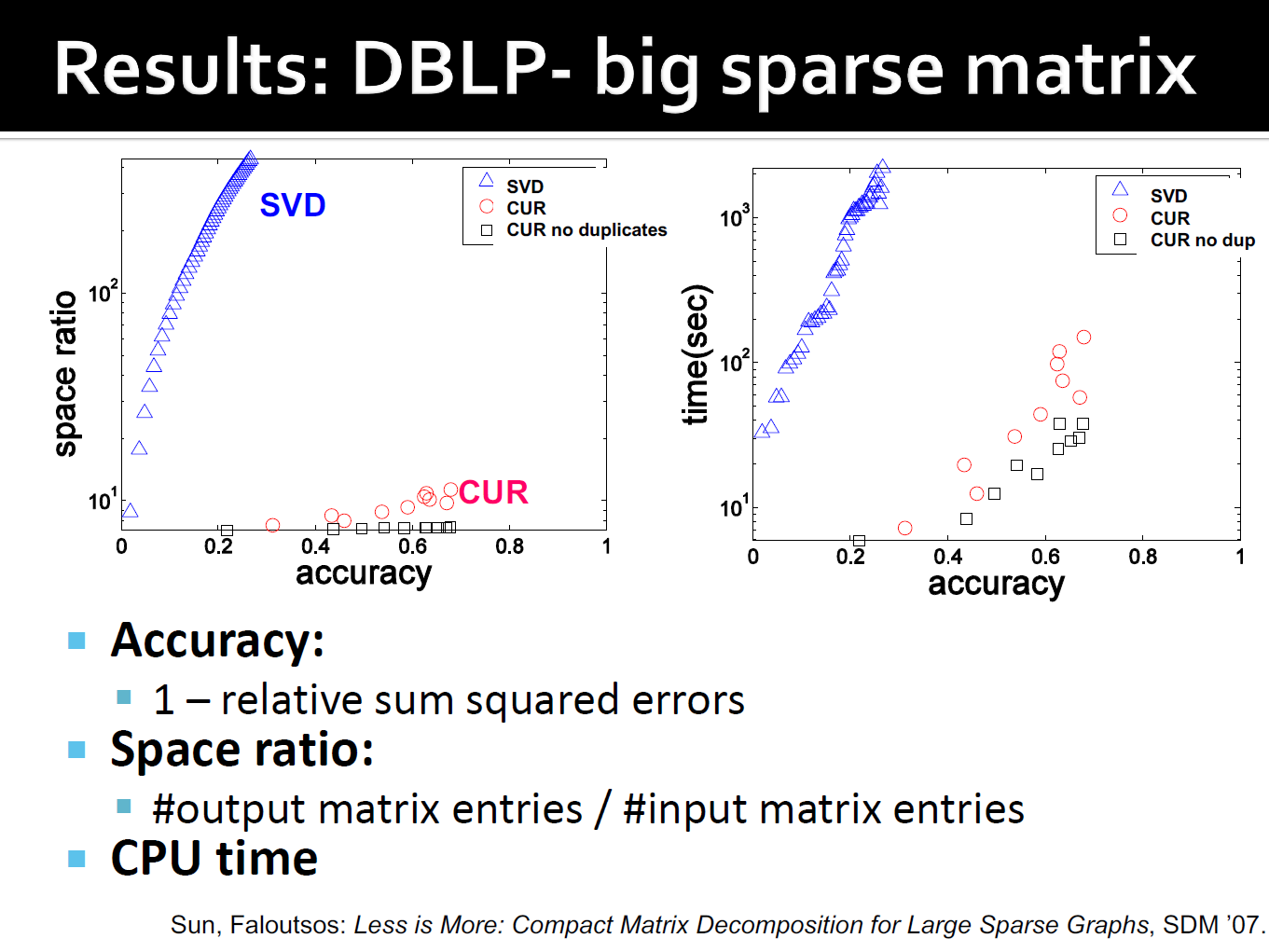
7. 线性假设

1. SVD只能用于线性投影:低维线性投影，保持欧式距离
2. 非线性方法:Isomap
   1. 数据位于一个低维的非线性曲线
   2. 使用距离度量对应的形状

8. 其他参考

1. 奇异值的物理含义是什么
2. 浅谈SVD分解和CUR分解