Lecture11-图挖掘-动机，应用和算法

1. 我们为什么会关注图数据

2. 参与的网络和社交媒体

2.1. 传统的媒体

广播：一对多，这些内容都是相对比较专业的

2.2. 社交媒体：多对多关系

交互提供了丰富的关于用户、内容的信息

2.2.1. 社交媒体的特点

每个人都可以成为媒体
通讯障碍消失
1. 丰富的用户互动
2. 用户生成的内容
3. 用户丰富的内容
4. 用户开发的小部件
5. 协作环境
6. 集体智慧
7. 长尾模式
广播媒体(过滤，然后发布) -> 社交媒体(发布，然后过滤)

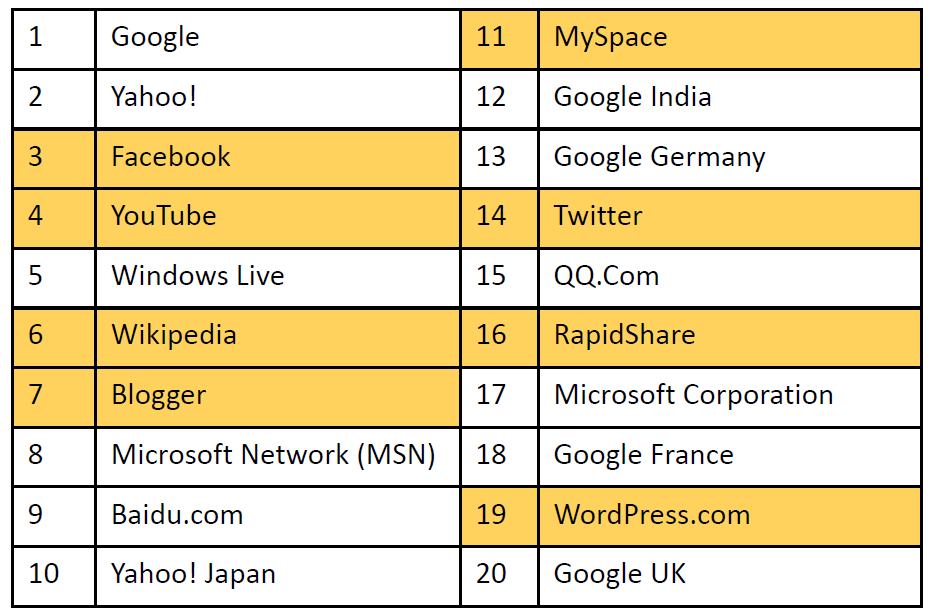
2.2.2. 最经常被访问的20个网页

前20个最常被访问的网站中有40%是社交网站

2.2.3. 社交网络有越来越重要的意义

美国大选

2.2.4. 社交网络

由节点(个人或组织)组成的社会结构，这些节点通过各种相互依存关系(如友谊，亲属关系等)相互关联。
图示
1. 节点：成员
2. 优势：关系
各种实现
1. 社交书签(Del.icio.us)
2. 友谊网络(facebook，myspace)
3. Blogosphere
4. 媒体共享(Flickr，Youtube)
5. 民间传说

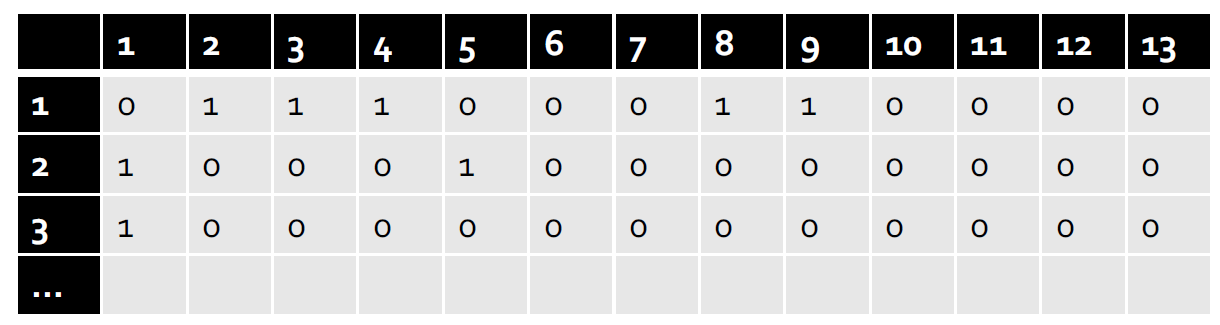
2.3. 社会矩阵

社交网络也可以矩阵形式表示

2.4. 社交计算和数据挖掘

社会计算涉及基于计算系统的社会行为和社会环境的研究。
数据挖掘相关任务
1. 集中度分析(中心和重点发现)
2. 社团检测
3. 分类
4. 关联预测
5. 病毒式营销
6. 网络建模
补充：城市计算

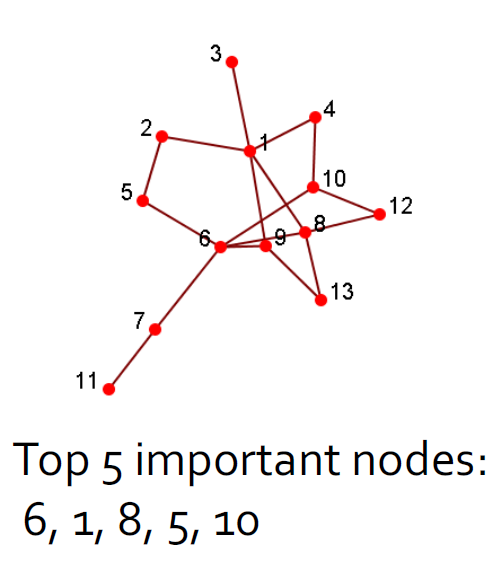
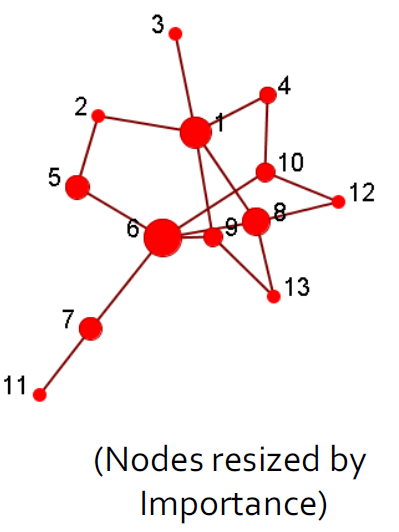
2.4.1. 集中性分析/影响力研究

识别社交网络中最重要的参与者
1. 给出：一个社交网络
2. 输出：顶级节点列表
计算出来任意两个节点之间的最近路径，然后计算出每一个节点相对于其他节点的是不是最近节点，得到中心度。
或者还可以使用1跳或者xxx来作为判断标准

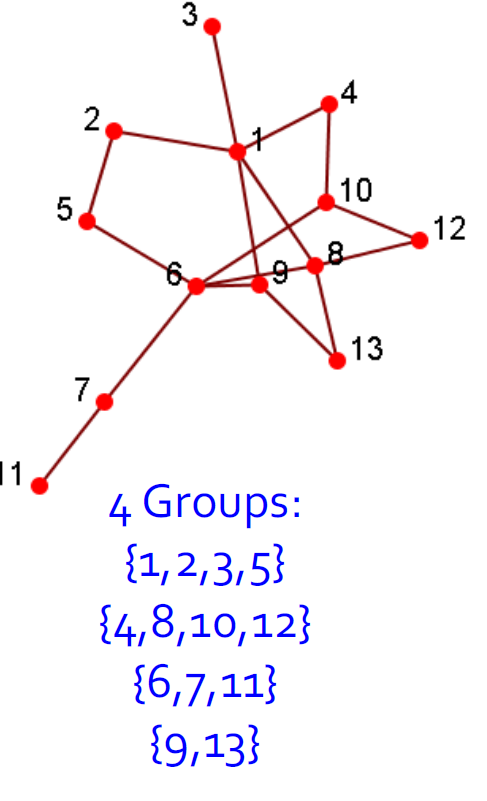
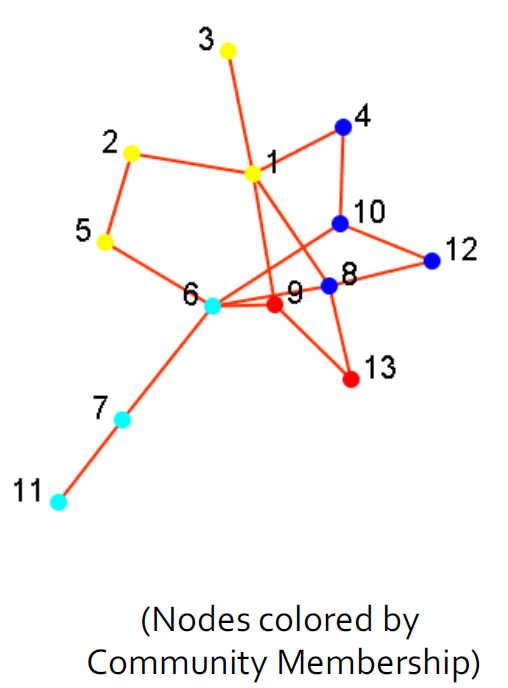
2.4.2. 社团检测(聚类)

社团是一组节点，它们之间的交互(相对)频繁(也称为组，子组，模块，集群)
社团检测又称分组，聚类，寻找有凝聚力的亚组(社团)，有点类似于聚类任务。
1. 给出：一个社交网络
2. 产出：(一些)演员的社团成员
应用
1. 了解人与人之间的互动
2. 可视化和导航大型网络
3. 为其他任务(例如数据挖掘)奠定基础
分组后可视化结果

2.4.3. 分类

用户首选项或行为可以表示为类标签
1. 是否点击广告
2. 是否对某些主题感兴趣
3. 订阅了某些政治观点
4. 喜欢/不喜欢产品
输入
1. 社交网络
2. 网络中一些参与者的标签
输出：网络中剩余参与者的标签
总结：分类预测后可视化

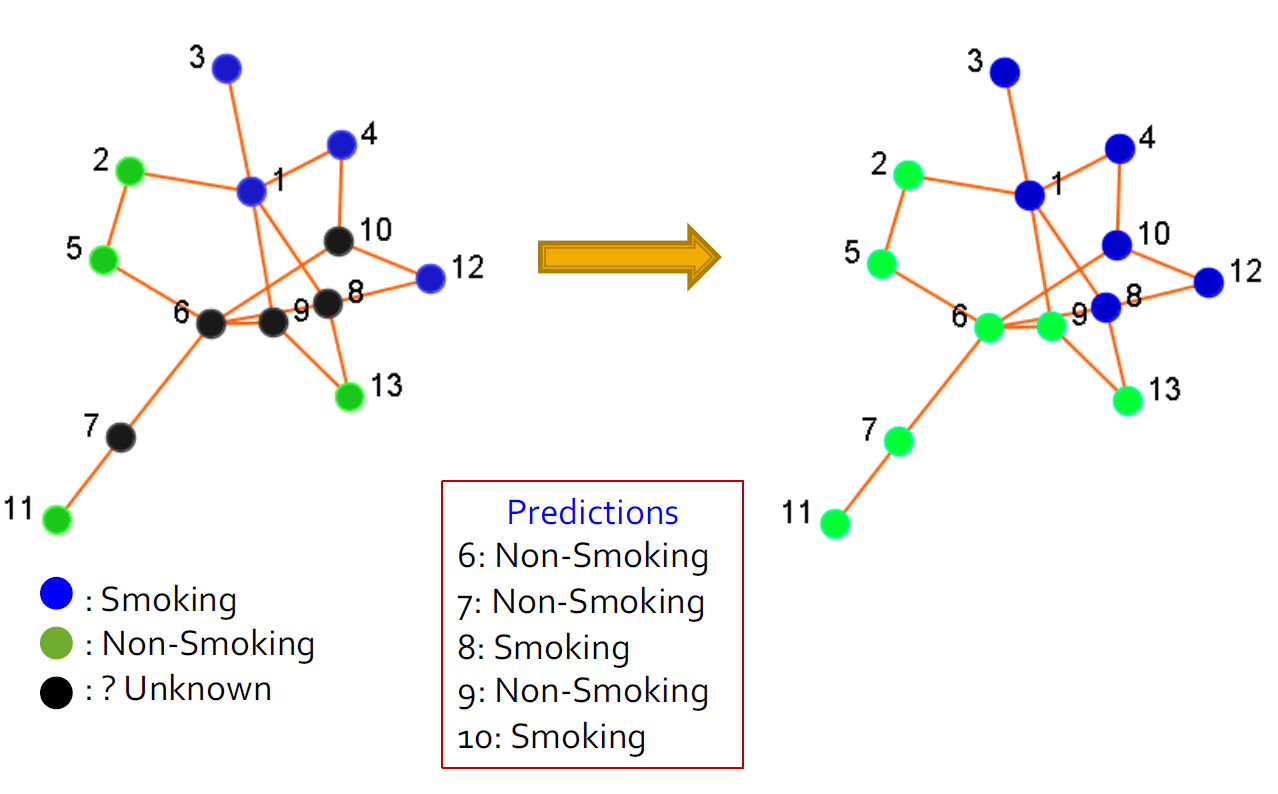
2.4.4. 关联预测

给定一个社交网络，预测哪些节点可能会连接
输出(排名)节点对的列表
示例：Facebook中的朋友推荐

2.4.5. 病毒式营销/爆发检测

2.4.5.1. 什么是病毒式营销/爆发检测

用户在社交网络中具有不同的社交资本(或网络价值)，因此，人们如何才能最好地利用这一信息？
病毒式营销：找出一组用户来提供优惠券和促销以影响网络中的其他人，从而使我的利益最大化
爆发检测：监控一组节点，这些节点可帮助检测爆发或中断感染传播(例如H1N1流感)
目标：在预算有限的情况下，如何最大程度地提高整体收益？

2.4.5.2. 病毒式营销的例子

查找节点数量最少的整个节点网络的覆盖范围
如何实现它，一个例子：基本贪婪选择：选择使实用程序最大化的节点，删除该节点，然后重复
1. 首先选择节点1
2. 然后选择节点8
3. 最后选择节点7，节点7不是一个有高中心度的结点。

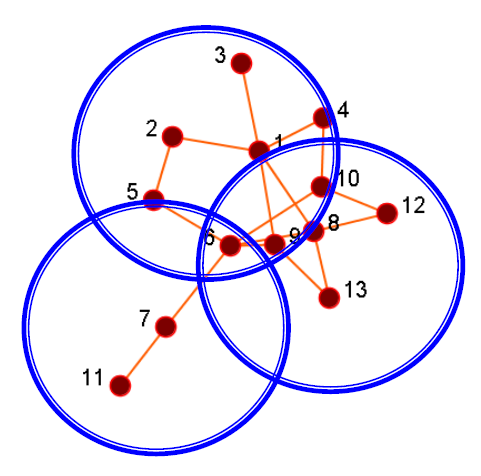
2.4.6. 网络建模

大型网络展示了统计模式：
1. 小世界效果(例如6度的分离度)
2. 幂律分布(又称无标度分布)
3. 社团结构(高聚集系数)
模拟网络动力学
1. 找到一种机制，以便可以复制在大型网络中观察到的统计模式。
2. 示例：随机图，优先附着过程
用于仿真以了解网络属性
1. Thomas Shelling的著名模拟：是什么导致白人和黑人隔离
2. 受攻击的网络稳健性
二八现象：20%的节点上有着80%的重要性
网络模型应用

2.5. 社交计算的应用

通过社交网络做广告
行为建模和预测
流行病学研究
协同过滤
人群情绪阅读器
文化趋势监测
可视化
健康2.0

3. 社团探测原则

3.1. 社团

社团：具有相对牢固，直接，强烈，频繁或积极联系的演员的子集。
社团是一组经常相互交流的参与者，例如：参加会议的人
一群没有互动的人不是一个社团，例如：人们在车站等公共汽车，却不互相交谈
人们在社交媒体中形成社团

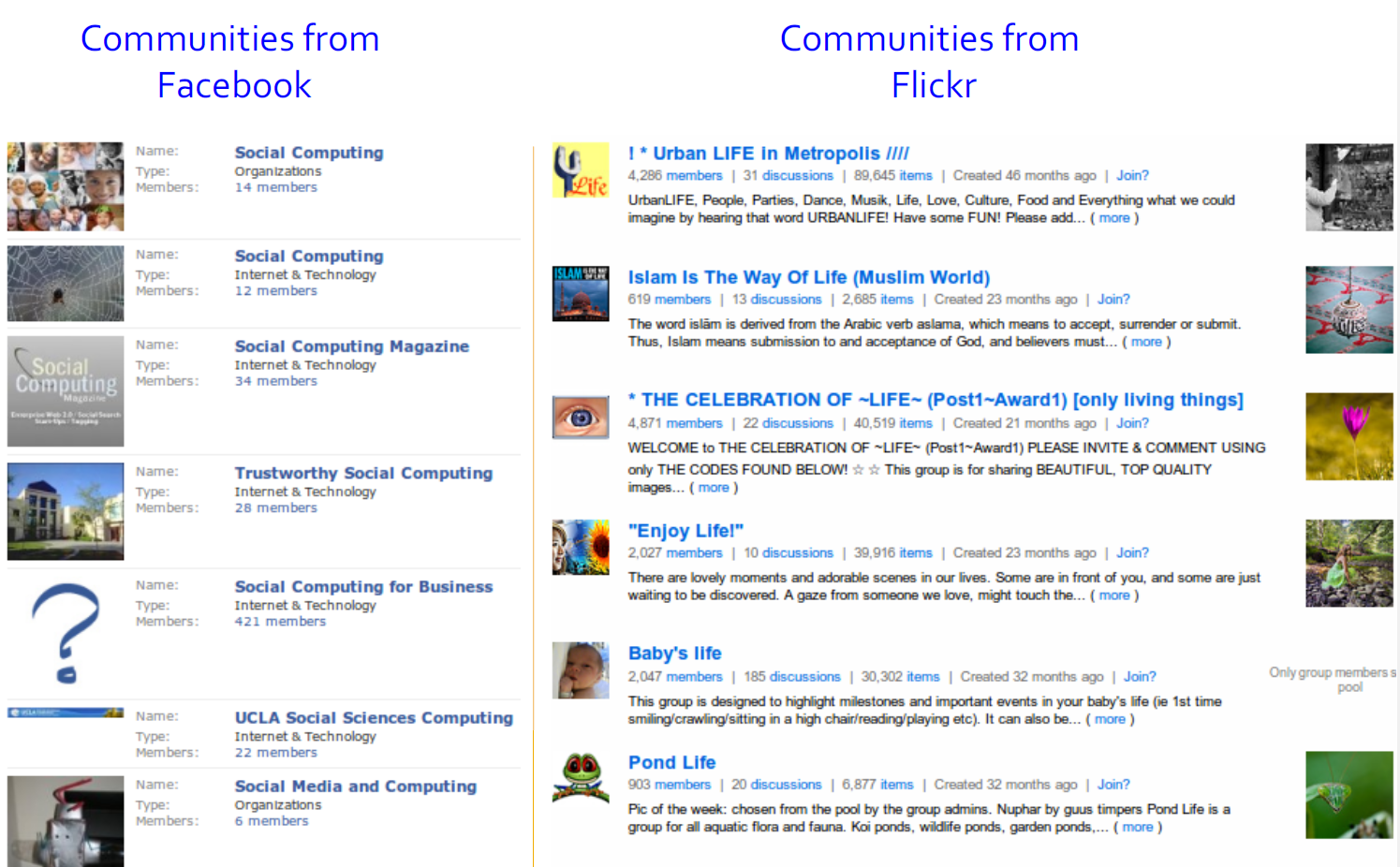
3.2. 社团的例子

3.3. 为什么在社交媒体上有社团

人是社会的
社交媒体中的部分互动是对现实世界的一瞥
人们在现实世界以及在线中都与朋友，亲戚和同事保持联系
易于使用的社交媒体使人们能够以前所未有的方式扩展社交生活，很难认识现实世界中的朋友，但更容易在网上找到志趣相投的朋友

3.4. 社团探测

社团检测：根据社交网络属性正式确定强大的社交群体
一些社交媒体网站允许人们加入群组，是否有必要根据网络拓扑提取群组？
1. 并非所有站点都提供社团平台
2. 并非所有人都参加
网络交互可提供有关用户之间关系的丰富信息
1. 组是隐式形成的
2. 可以补充其他类型的信息
3. 帮助网络可视化和导航
4. 提供其他任务的基本信息
社团定义的主观性

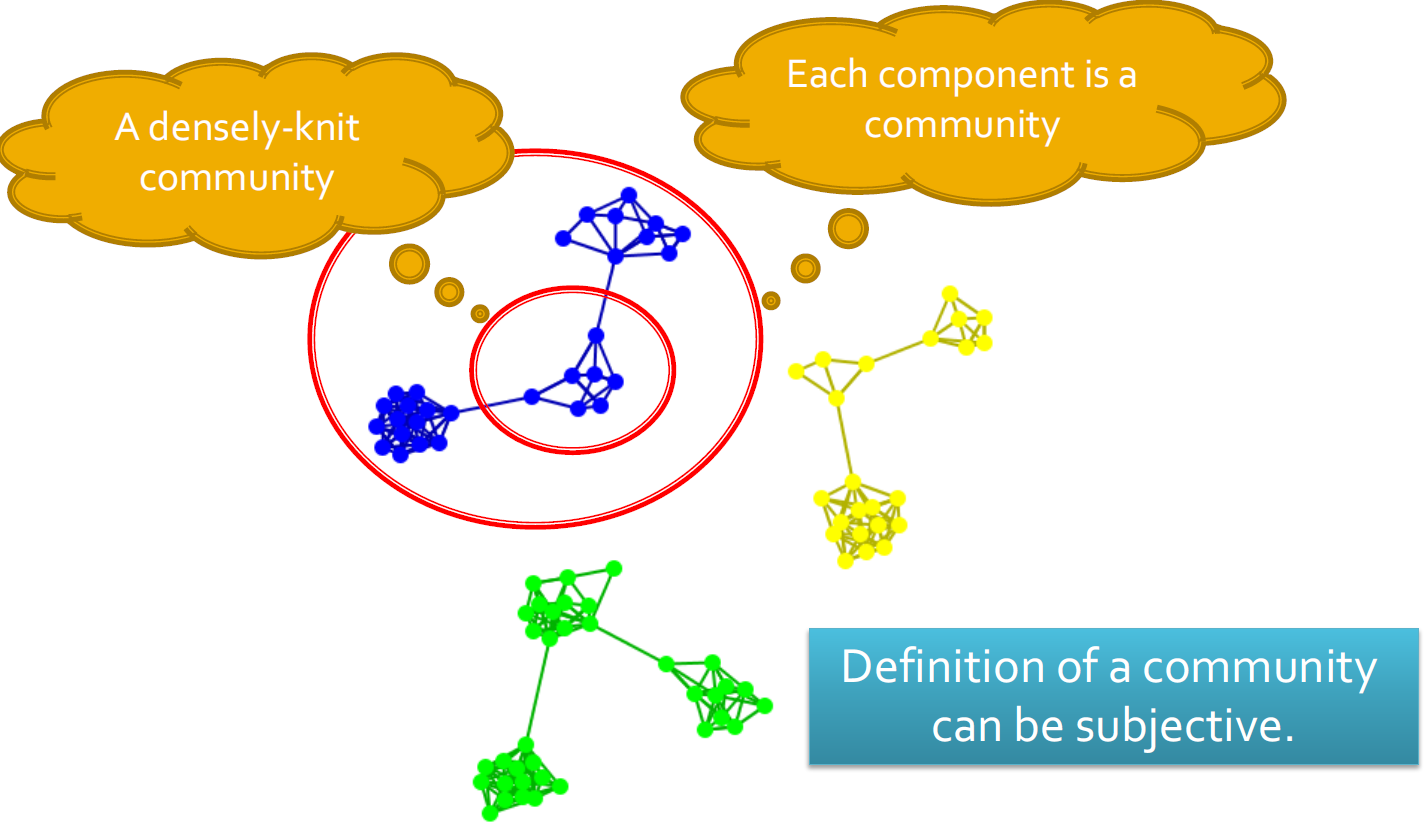
3.5. 社团标准分类

条件因任务而异
大致上，社团检测方法可分为4类(非排他性)：
1. 以节点为中心的社团：组中的每个节点都满足某些属性
2. 以团体为中心的社团：考虑整个组内的连接。该组必须满足某些属性，而无需放大节点级别
3. 以网络为中心的社团：将整个网络分成几个不相交的集合
4. 以等级为中心的社团：构建社团的层次结构

3.5.1. 以节点为中心的社团探测

节点满足不同的属性
1. 完全互通：clique
2. 成员可达性：k-clique，k-clan，k-club
3. 节点度：k-plex，k-core
4. 内外关系的相对频率：LS集，Lambda集
在传统社交网络分析中常用

3.5.1.1. 完全互通：clique

Clique:三个或更多节点彼此相邻的最大完整子图
NP-hard问题：以找到网络中的最大clique，直接实现查找clique会是一个非常耗时的操作
通常会从clique出发去探索更大的clique
递归修剪：
1. 从给定网络中采样一个子网，然后通过贪婪的方法在该子网中找到一个clique
2. 假设上面的clique大小为k，为了找到更大的clique，应删除度数<= k-1的所有节点。
重复上诉操作直到网络足够小。
随着社交媒体网络遵循节点度的幂定律分布，许多节点将被修剪

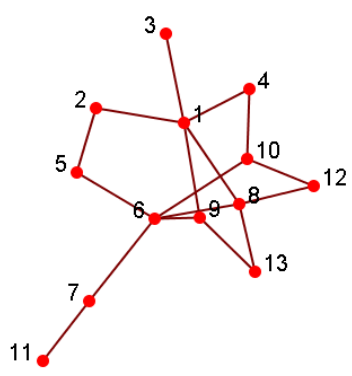
假设我们对一个节点为{1-9}的子网进行采样，并找到一个大小为3的集团{1,2,3}
为了找到>3的集团，请删除所有具有度数小于2(3-1)的节点
- 删除节点2和9
- 删除节点1和3
- 删除节点4

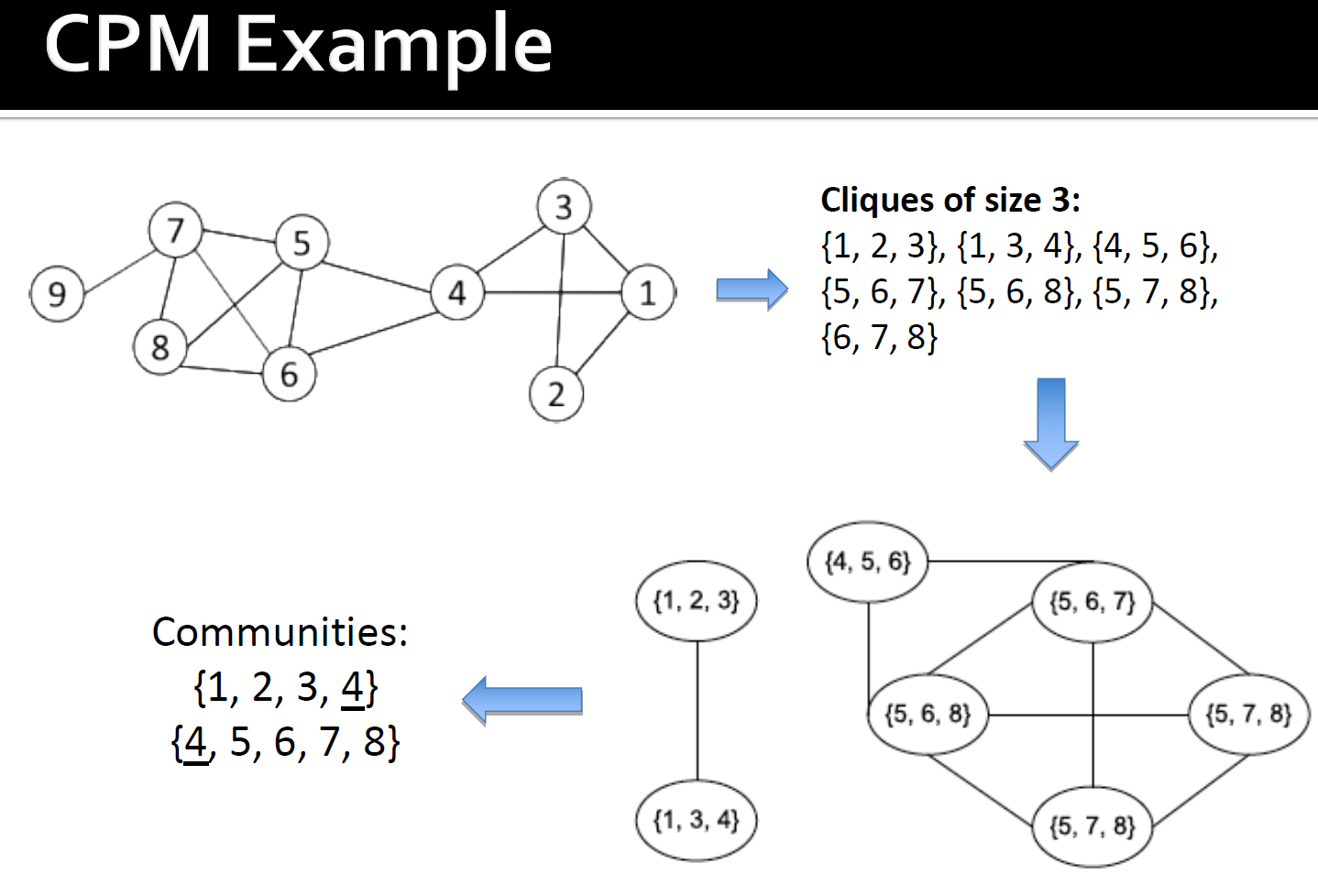
3.5.1.2. Clique渗透方法(CPM)

Clique是非常严格的定义，不稳定
通常以Clique为核心或种子来寻找更大的社团
CPM是查找重叠clique的一种方法
输入：参数k和网络
过程
1. 找出给定网络中所有大小为k的clique
2. 构造clique图。如果两个派系共享k-1个节点，则它们相邻
3. 集团图中的每个连接组件都构成一个社团

区别社团和clique

3.5.1.3. Geodesic

可达性通过Geodesic距离进行校准
Geodesic：两个节点(12和6)之间的最短路径
1. 两条路径：12-4-1-2-5-6、12-10-6
2. 12-10-6是Geodesic
Geodesic距离：在两个节点之间的Geodesic距离，例如，d(12，6)= 2，d(3，11)= 5
直径：网络中任意2个节点的最大测地距离，最长路径最短的跳跃

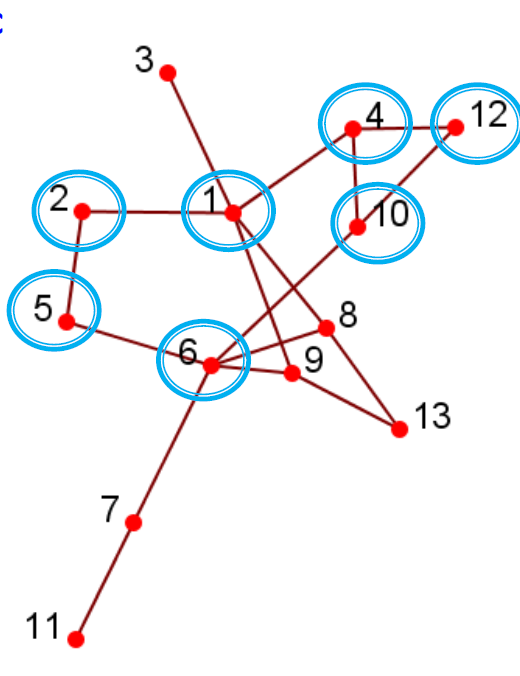
3.5.1.4. 可达性:k-clique、k-club

组中的任何节点都应在k跳中可达
k-clique：最大子图，其中任何节点之间的最大Geodesic距离<=k，但是其直径可能会超过k
k-club:直径小于等于k的子结构

上图中的2-clique：{12，4，10，1，6}
上图中的2-club：{1,2,5,6,8,9}，{12，4，10，1}
直径可能会更大:子图d(1，6)= 3中
经常在传统SNA中使用

3.5.2. 以团体为中心的社团

以组为中心的标准要求整个组满足一定条件，例如，组密度>=给定阈值
考虑整个组中的连接，可以使某些节点的连接性低
对于有 $V_s$ 个节点和 $E_s$ 条边的图 $G_s(V_s, E_s)$ 是一个密度为 $\gamma$ 的quasi-clique，如果满足

\frac{E_s }{\frac{V_s(V_s - 1)}{2}} \geq \gamma

分母是最大度数

递归修剪：
1. 对子图进行采样，找到最大的 $\gamma$ 密集拟似云(结果大小= k)
2. 删除满足以下条件的结点
  1. 度小于 $k\gamma$
  2. 所有的邻居的度都小于 $k\gamma$
采样一个子图，并找到一个最大的 $\gamma-dense$ quasi-clique(比如 $|V_s|$ 的大小)
删除度数小于平均度数的节点

< |V_s|\gamma \leq\frac{2|E_s|}{|V_s|-1}

3.5.3. 以网络为中心的社团

要形成一个组，我们需要全局考虑节点的连接。
目标：将网络划分为不相交的集合
1. 基于节点相似性的组
2. 基于潜在空间模型的组
3. 基于块模型近似的组
4. 基于切割最小化的组
5. 基于模块化最大化的组

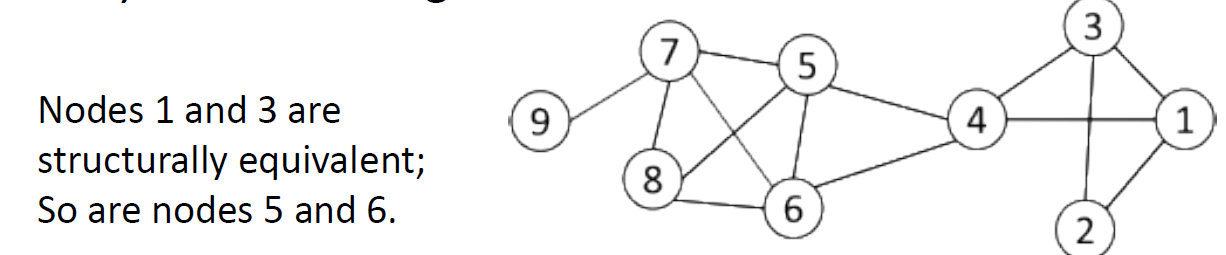
3.5.3.1. 节点相似度

节点相似性由它们的交互模式有多相似来定义，对节点应用k均值或基于相似度的聚类。
如果两个节点连接到同一组参与者，则在结构上是等效的。例如，节点8和9在结构上等效
组是在等效节点上定义的：过于严格、很少大规模放生、宽松的等价类很难计算
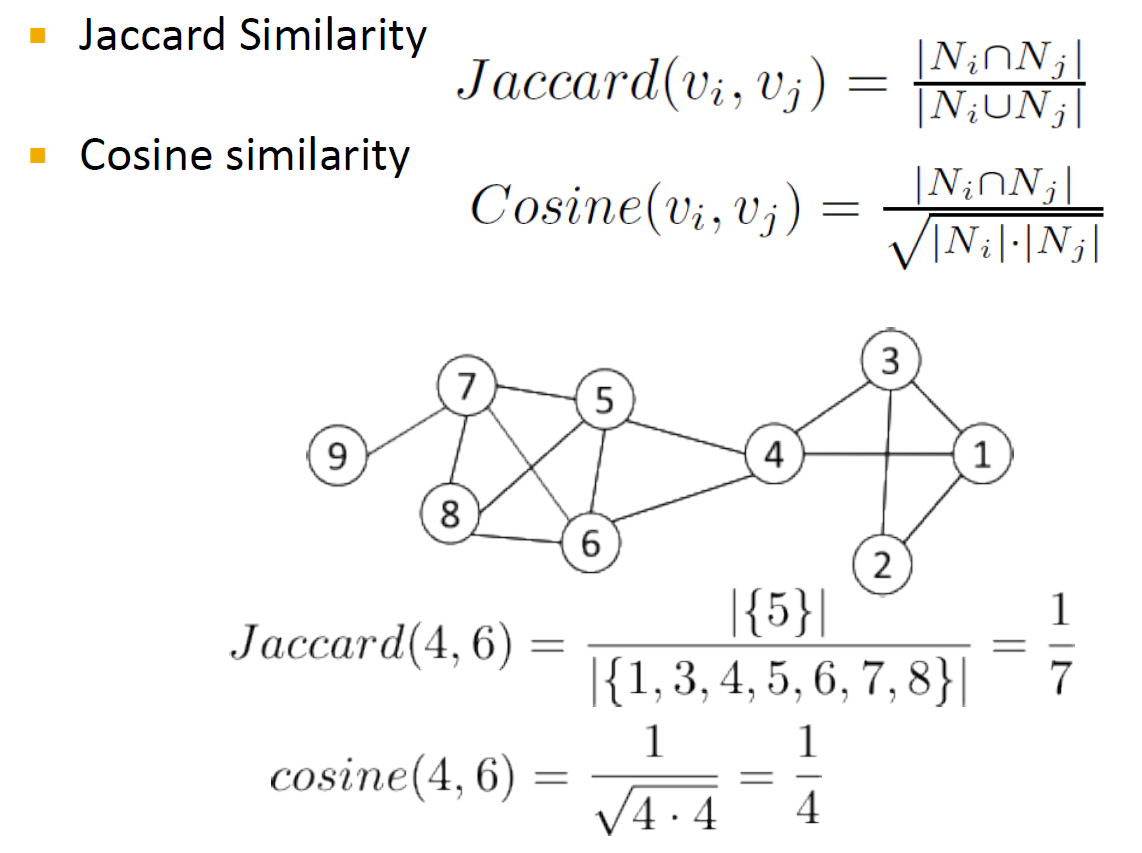
实际上，使用向量相似度：例如，余弦相似度，Jaccard相似度

3.5.3.2. 向量相似度

Cosine Similarity

similarity = \cos(\theta) = \frac{A \cap B}{||A||*||B||} \\ sim(5,8) = \frac{1}{\sqrt{2} * \sqrt{3}} = \frac{1}{\sqrt{6}} \\

Jaccard Similarity

J(A, B) = \frac{|A \cap B|}{|A \cup B|} \\ J(5, 8) = \frac{|\{6\}|}{|\{1, 2, 6, 13\}|} = \frac{1}{4} \\

3.5.3.3. 基于节点相似度的聚类

对于大型网络的实际使用：
1. 将连接视为特征
2. 使用余弦或Jaccard相似度计算顶点相似度
3. 应用经典的k均值聚类算法
K均值聚类算法：
1. 每个聚类与一个质心(中心点)相关联
2. 将每个节点分配给具有最接近质心的群集

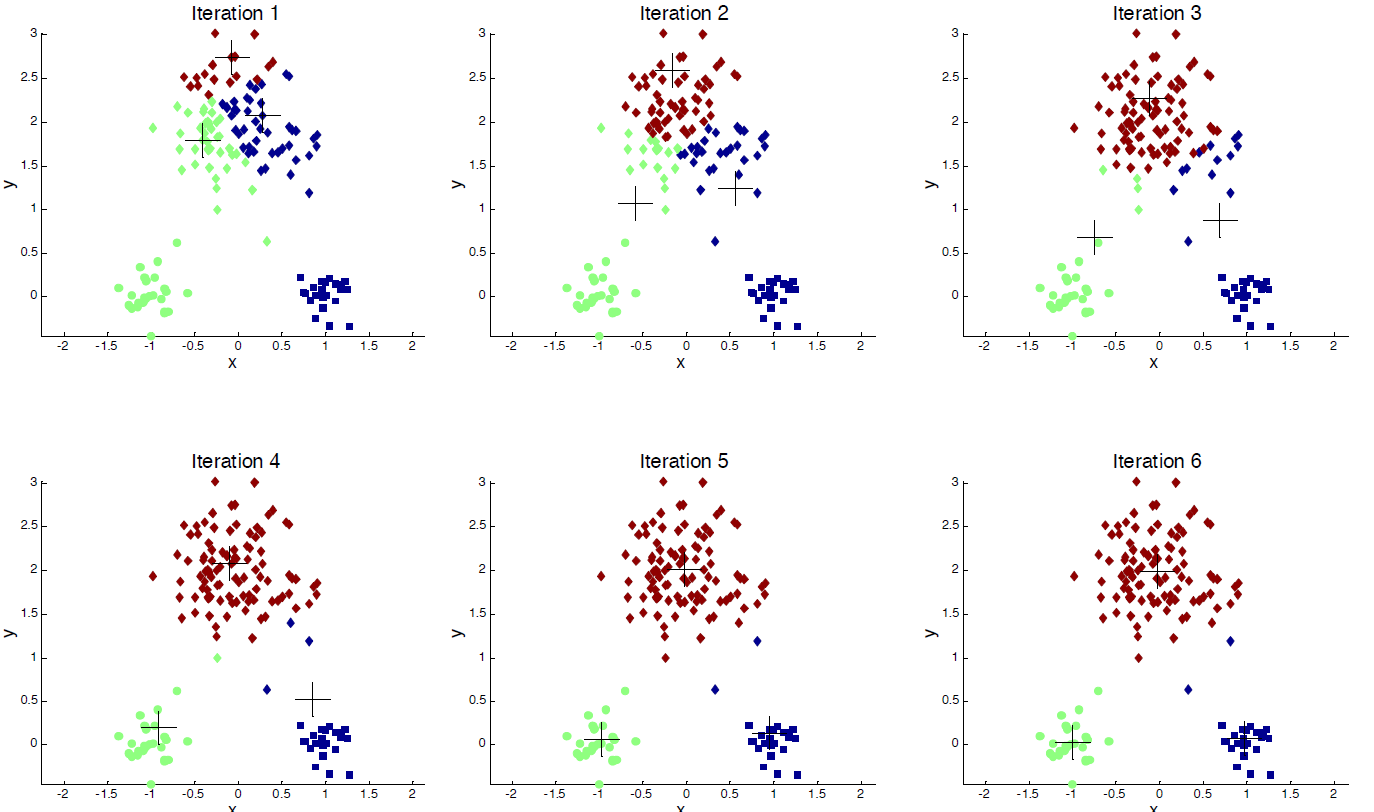
3.5.3.4. 潜在空间模型上的组

潜在空间模型：将网络中的节点转换为较低维度的空间，以使节点之间的距离或相似性保持在欧几里得空间中
将k均值应用于S以获取聚类

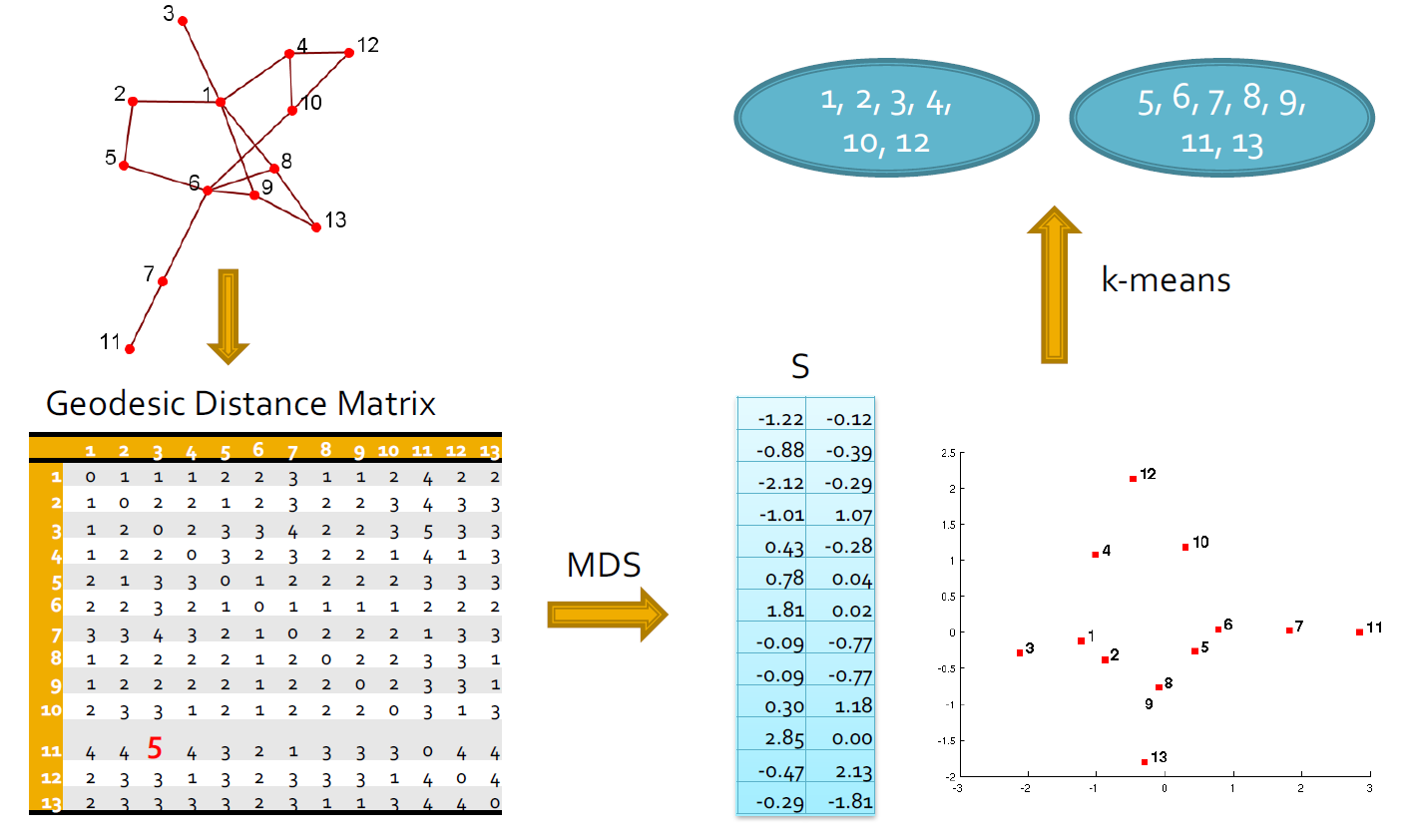
3.5.3.5. 多维缩放(MDS)

给定一个网络，构造一个接近矩阵来表示节点之间的距离(例如geodesic距离)
令D表示节点之间的平方距离
$S \in R^{n * k}$ 表示低维空间中的坐标

SS^T = -\frac{1}{2} *(I - \frac{1}{n}e*e^T)D(I - \frac{1}{n}e*e^T) = \triangle(D)

客观性:最小化差异 $\min||\triangle(D) - SS^T||_F$
我们计算 $\Epsilon = diag(\lambda_1, ... , \lambda_k)$ 的前k个特征值，V前k个特征向量
解决方案: $S = V * \Epsilon^{\frac{1}{2}}$
例子:

3.5.3.6. 块模型近似

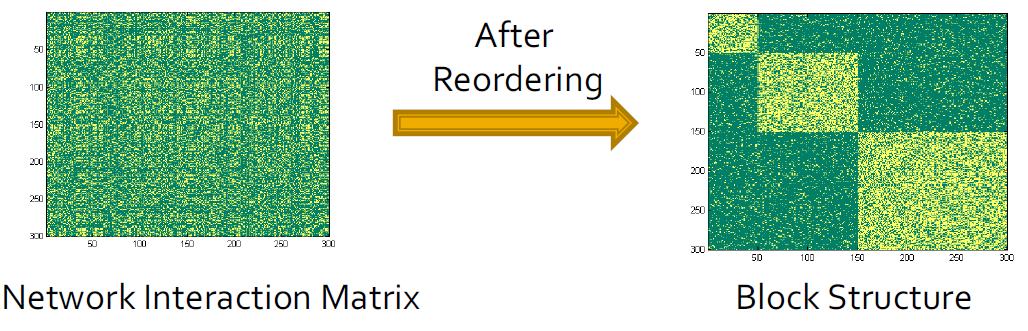
客观上，最小化两个矩阵之间的差异

\min\limits_{S, \Sigma}||A - S \Sigma S^T||_F \\ s.t.\ S \in{0, 1}^{n * k}, \Sigma \in R^{k * k} is\ diagonal

挑战：S是离散的，很难去求解
放松：允许S连续满足 $S^TS = I_k$
解决方案：使用矩阵A的特征值
后处理：将k均值应用于S以找到分区

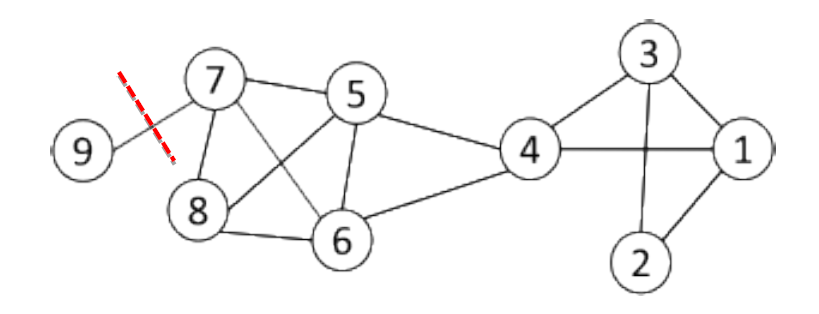
3.5.3.7. 最小化切割

大多数互动都在小组内部，而小组之间的互动很少
我们将社团检测简化为最小切割问题
剪切：将图的顶点划分为两个不相交的集合
目标：最小割问题，找到一个图形分区，以使两组之间的边数最小化
1. 限制:经常会找到只有一个结点的社团
2. 需要去考虑组的大小

cut(C_1, C_2, C_3, ..., C_k) = \sum\limits_{i = 1}\limits^{k}cut(C_i, \overline{C_i})

3.5.3.8. 经常使用的切割方式

最小切割通常会返回不平衡的分区，其中一组是单例，例如节点9

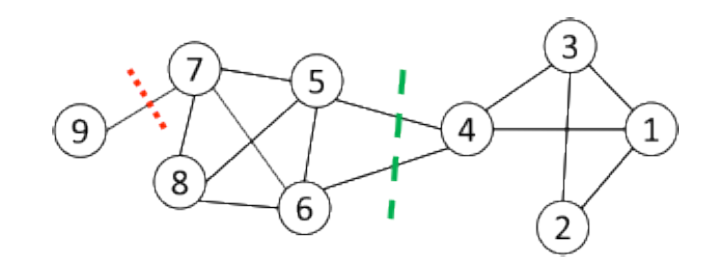
更改目标函数以考虑社区规模
Ratio-cut:在网络中的结点数量
Normalized-cut:在组内的结点的相关性

Ratio-cut(C_1, C_2,... , C_k) = \sum\limits_{i=1}\limits^k\frac{cut(C_i, \overline{C_i})}{|V_i|} \\ Normalized-cut(C_1, C_2, ... , C_k) = \frac{1}{k}\sum\limits_{i = 1}\limits^{k}\frac{cut(C_i, \overline{C_i})}{vol(V_i)}

$C_i$ 是一个社团
$|C_i|$ 是 $C_i$ 中的结点数
$vol(C_i)$ 是 $C_i$ 中的结点的度总数，包含切断的边

3.5.3.9. 图拉普拉斯算子

可以被花间为如下的最短路径问题
L是(规范化)图拉普拉斯算子

\min\limits_{S \in R^{n * k}} Tr(S^TLS)\ s.t. S^TS = I \\ L = D - A \\ D = \begin{bmatrix} d_1 & 0 & ... & 0 \\ 0 & d_2 & ... & 0 \\ . & . & . & . \\ . & . & . & . \\ . & . & . & . \\ 0 & 0 & ... & d_n \\ \end{bmatrix} \\ \ \\ normalized-L = I - D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \\

解决方案：S是具有最小特征值的L的特征向量(第一个特征除外)
后处理：将k均值应用于S，亦称光谱聚类

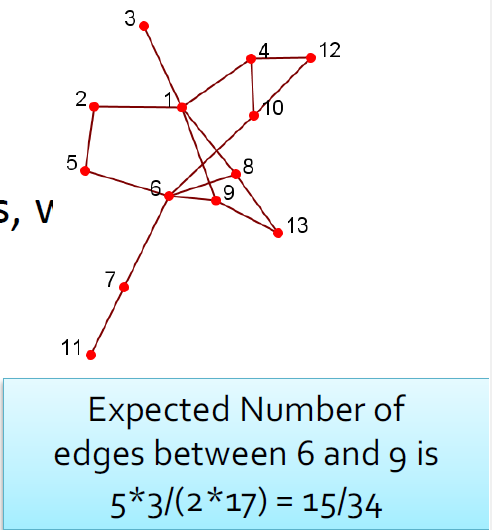
3.5.3.10. 模块化最大化

模块化通过考虑度数分布来度量社区划分的强度。给定一个具有m个边的网络，度为 $d_i$ 和 $d_j$ 的两个节点之间的期望边数为

\frac{d_i * d_j}{2 * m}

社团的强度：

\sum\limits_{i \in C, j \in C} (A_{ij} - \frac{d_id_j}{2m})

模块化：较大的值表示社区结构良好

\max \frac{1}{2m}\sum\limits_C\sum\limits_{i\in C，j\in C} A_{ij} - \frac{d_id_j}{2m}

3.5.3.11. 模块矩阵

模块化最大化也可以用矩阵形式表示

Q=\frac{1}{2m}Tr(S^TBS)

B是模块化矩阵

B_{ij} = A_{ij} - \frac{d_id_j}{2m}

解决方案：模块化矩阵的顶部特征向量

3.5.3.12. 矩阵分解形式

对于潜在空间模型，块模型，频谱聚类和模块化最大化
可以表述为

\max(\min)_S\ Tr(S^TXS) \\ s.t. S^TS = I

3.5.3.13. 回顾以网络为中心的社团

以网络为中心的社团检测
1. 基于节点相似性的组
2. 基于潜在空间模型的组
3. 基于切割最小化的组
4. 基于块模型近似的组
5. 基于模块化最大化的组
目标：将网络节点划分为几个不相交的集合
限制：要求用户事先指定社团数

3.5.4. 以等级为中心的社团

目标：基于网络拓扑构建社团的层次结构
便于以不同的分辨率进行分析
代表性方法：
1. 划分层次聚类
2. 聚集层次聚类

3.5.4.1. 划分层次聚类

划分层次聚类
1. 将节点分成几组
2. 每组进一步分成较小的组
3. 以网络为中心的方法可以应用于分区
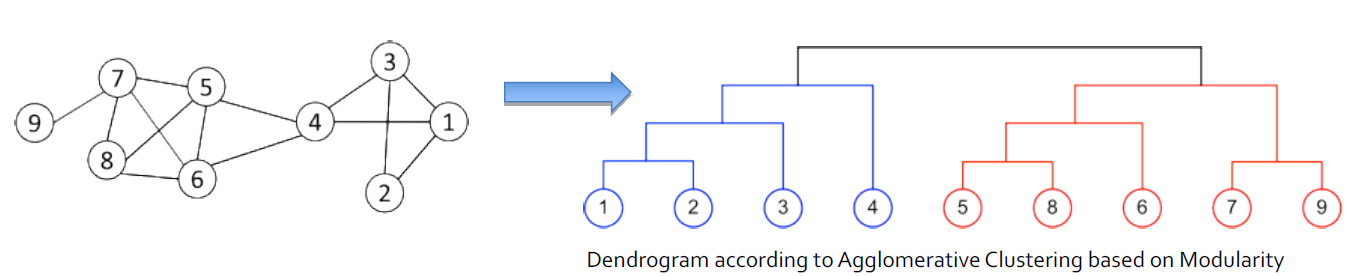
一个特定的例子:递归删除"最弱"的连接
1. 找到强度最小的边
2. 移除边并更新每个边的相应强度
递归上面的两个步骤，直到网络已经被分解成目标个数的联通图数
每一个连通图都构成一个社区

3.5.4.2. edge betweenness

边的强度可以通过边之间的距离来衡量
edge betweenness：通过该边的最短路径的数量
具有较高中间性的betweenness往往是两个社区之间的桥梁。

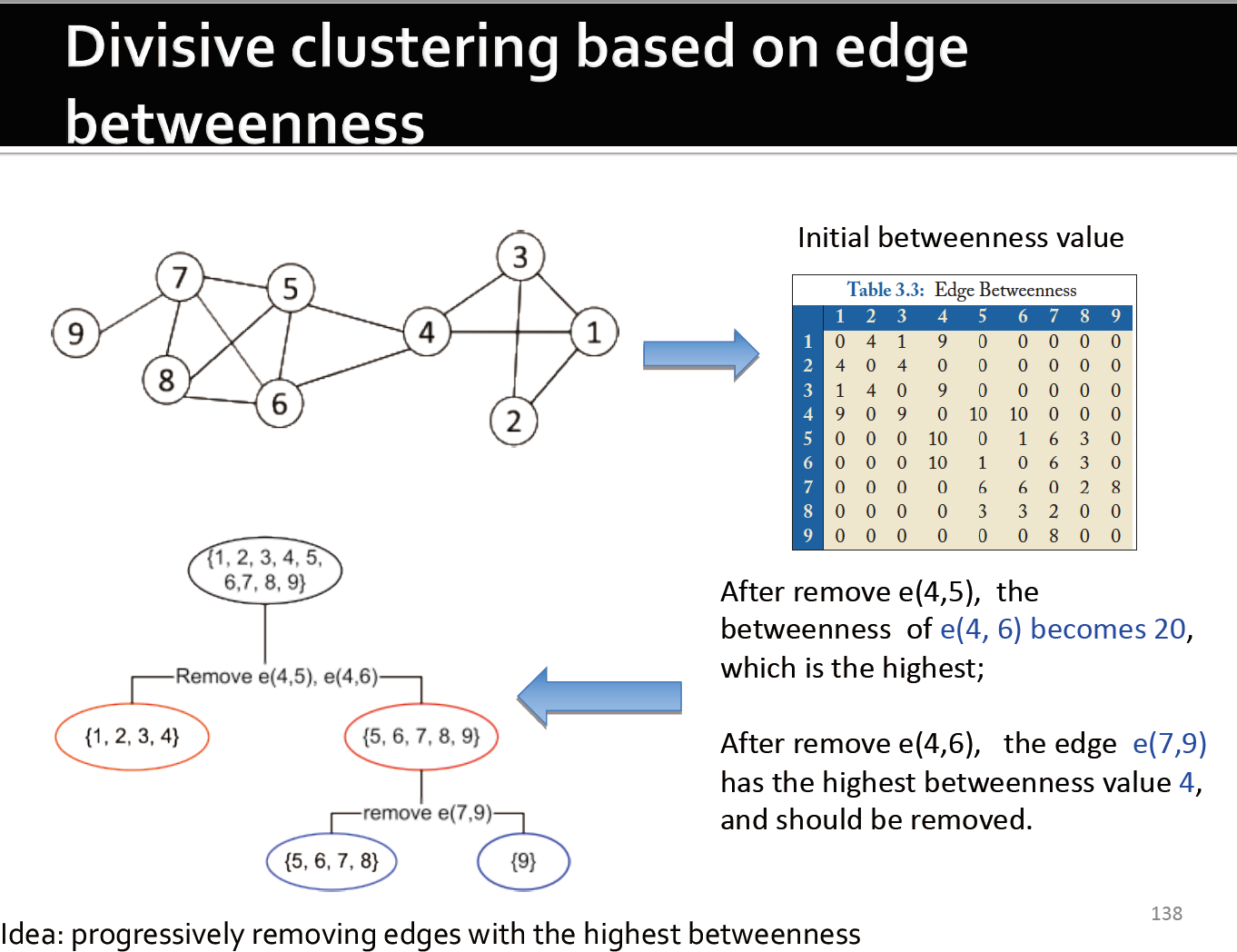
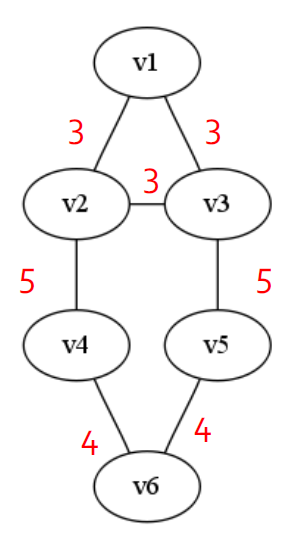
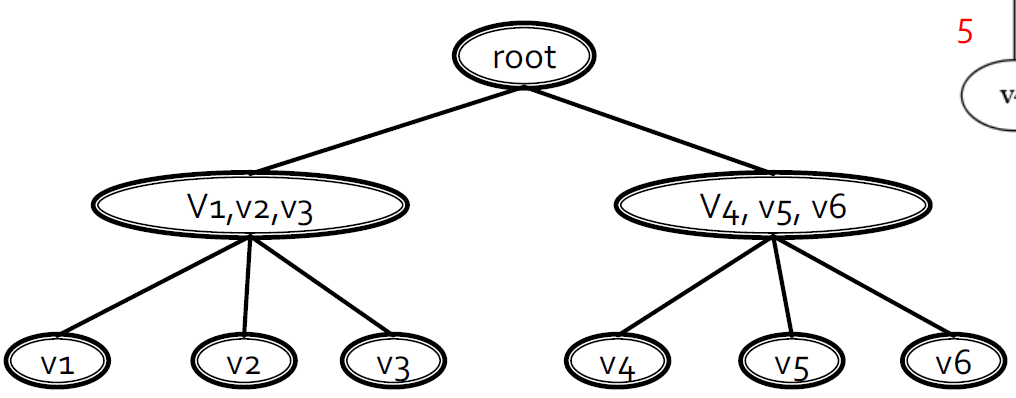
3.5.4.3. 根据edge betweenness来进行划分簇

逐步删除有最高的edge betweenness的边
1. 删除e(2, 4), e(3, 5)
2. 删除e(4, 6), e(5, 6)
3. 删除e(1, 2), e(2, 3), e(3, 1)

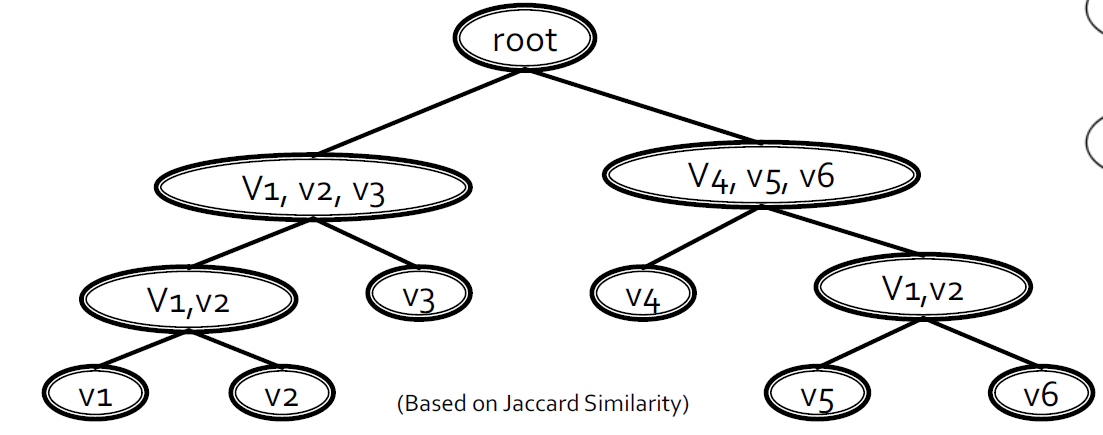
3.5.4.4. 聚集层次聚类

将每个节点初始化为社团
选择两个满足特定条件的社团，然后将它们合并为更大的社团
1. 最大模块化增加
2. 最大节点相似度

3.5.4.5. 回顾层次聚类

大多数分层聚类算法输出二叉树
1. 每个节点都有两个子节点
2. 可能高度失衡
聚集集群对节点的处理顺序和采用的合并标准非常敏感。
分裂聚类更稳定，但通常计算量更大

3.6. 社团探测总结

最佳方法？
根据应用程序，网络，计算资源等的不同而不同。
可扩展性可能是社交媒体网络的关注点
其他研究领域
1. 定向网络中的社团
2. 重叠的社团
3. 社团发展
4. 组分析和解释

4. 图数据挖掘

4.1. 数据挖掘

数据挖掘也称为数据库知识发现(KDD，Knowledge
Discovery in Databases)，是一种以无监督的方式从大型数据库中提取有用的隐藏信息的过程。

4.2. 类别任务

图模式挖掘
1. 挖掘频繁的子图模式
2. 图形索引
3. 图相似搜索
图形分类
1. 基于图模式的方法
2. 机器学习方法
图聚类：基于链路密度的方法

4.3. 图模式挖掘

频繁子图：如果(子)图在给定数据集中的支持(发生频率)不小于最小支持阈值，则该图频繁
对图g的支持定义为G中以g为子图的图的百分比
图形模式挖掘的应用
1. 挖掘生化结构
2. 程序控制流分析
3. 挖掘XML结构或Web社团
4. 用于图分类，聚类，压缩，比较和相关性分析的构建块

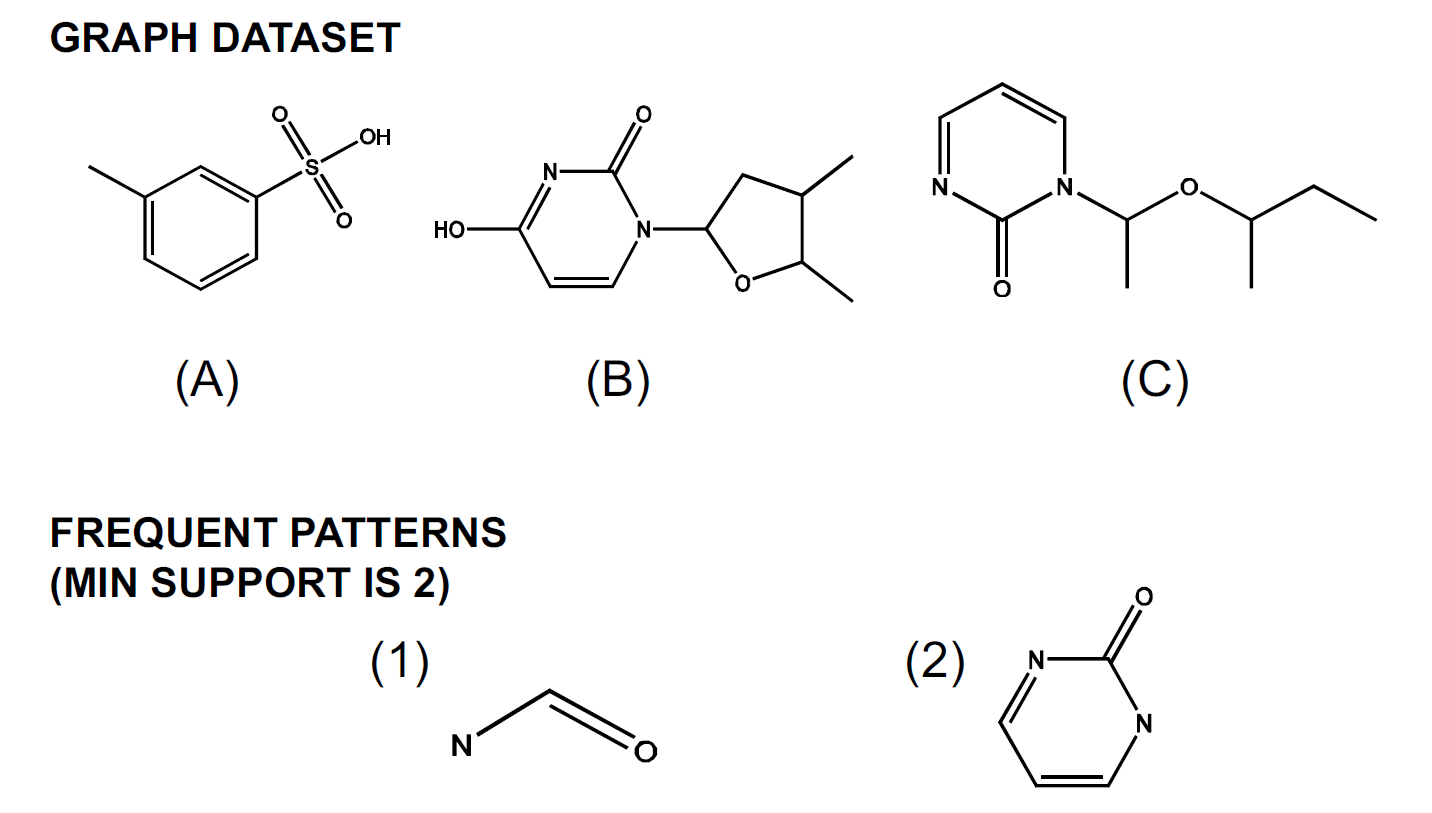
4.4. 示例:频繁子图

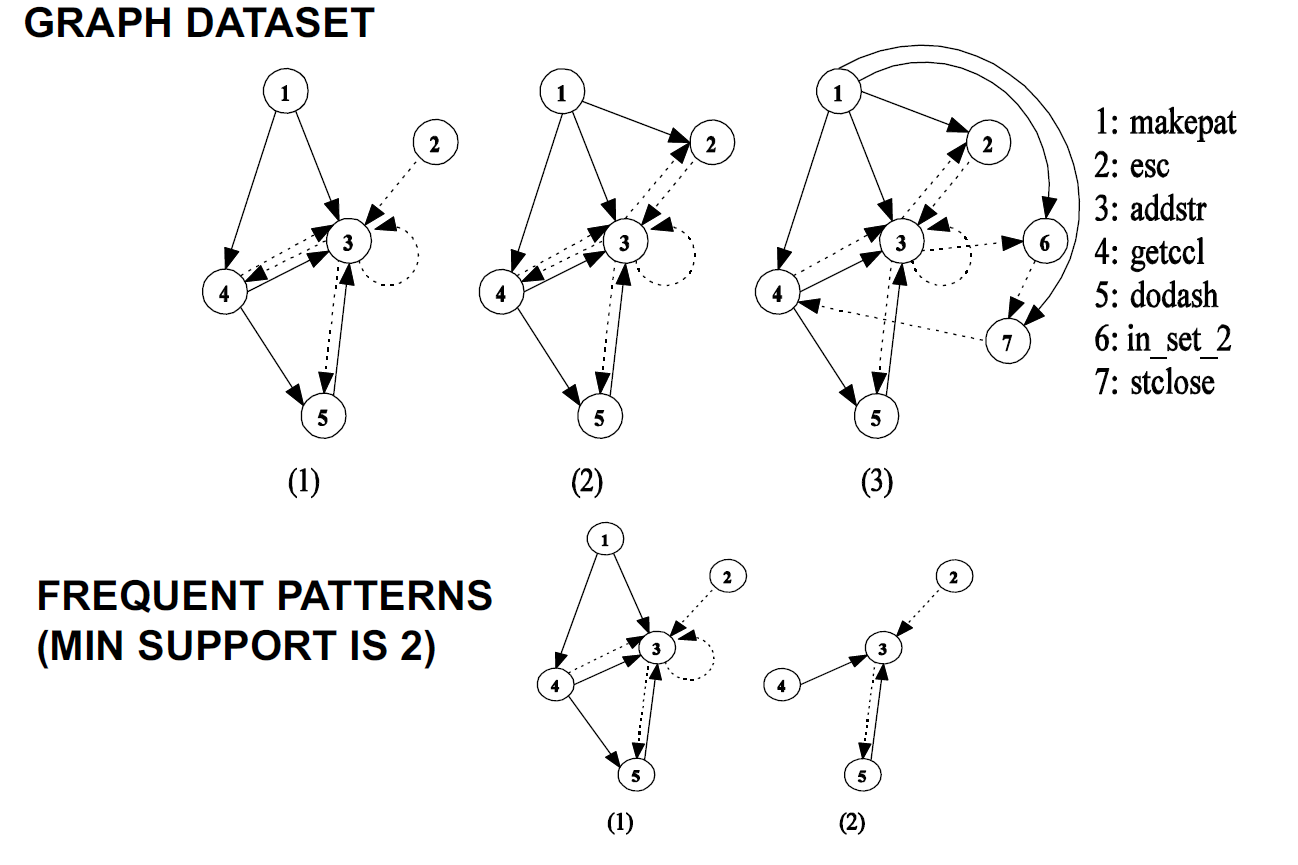4.5. 图挖掘算法

不完全的光束搜索:贪婪(制服)
归纳逻辑编程(WARMR)
基于图论的方法
1. 基于先验的方法
2. 模式增长法

4.6. 图挖掘算法的性质

搜索顺序：宽度与深度
生成候选子图：先验与模式增长
消除重复的子图：被动与主动
支持计算：是否嵌入商店
发现花样顺序：path->tree->graph

4.7. 基于先验的方法

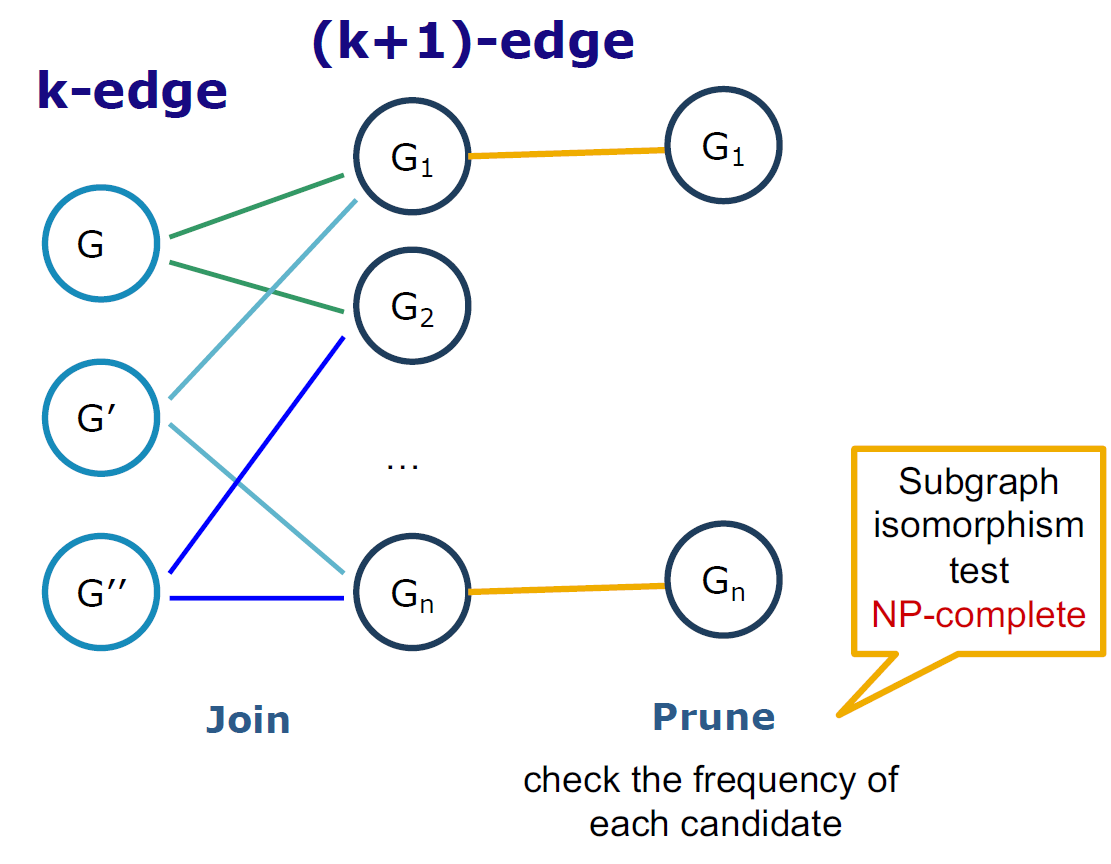
4.7.1. 例子

4.7.2. 基于先验，广度优先搜索

方法：广度搜索，连接两个图

年度股东大会(Inokuchi等)：生成一个带有另外一个节点的新图形

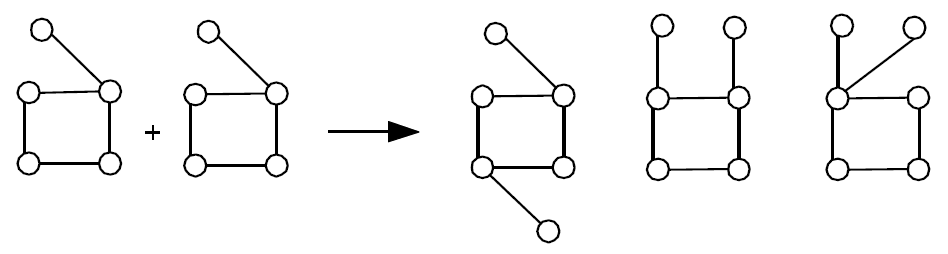
FSG(Kuramochi和Karypis)：生成具有更多边的新图

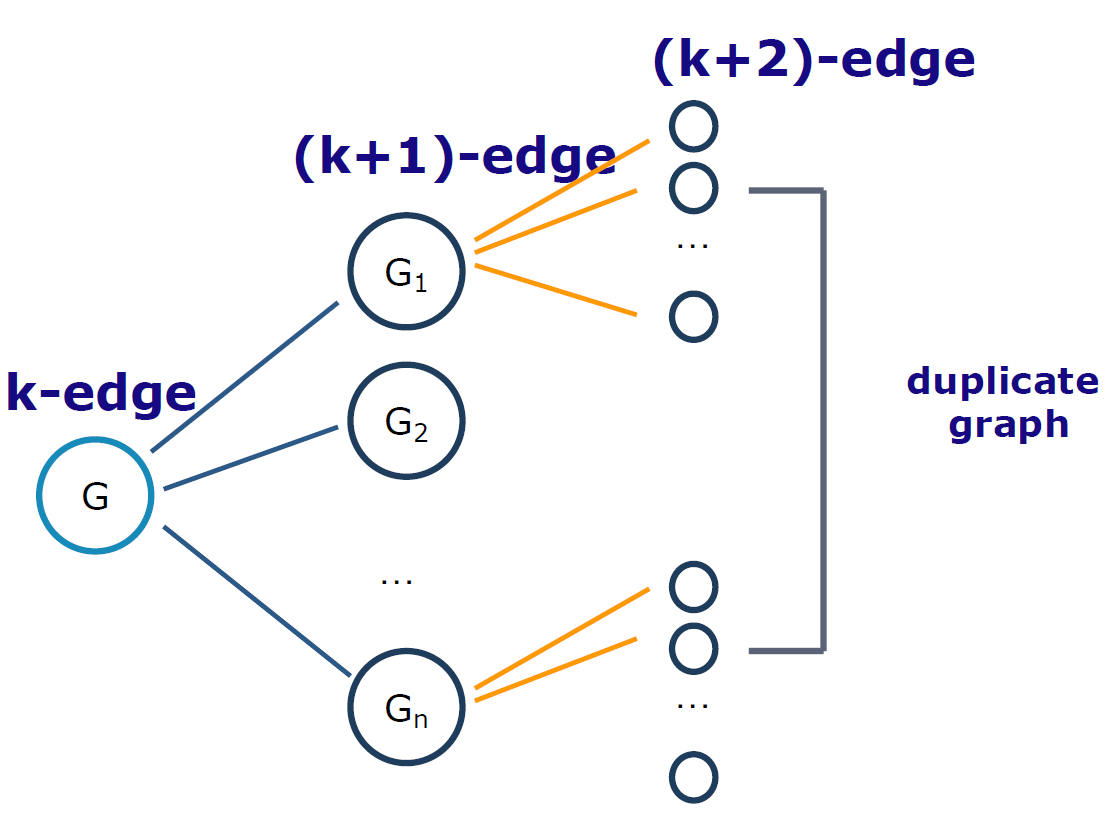
4.8. 模式增长算法

4.9. Transaction setting:GM的不同方法

4.9.1. 交易设定

输入(D, minSup)
1. 带有标签的图形交易记录集 $D = {T_1，T_2，...，T_N}$ ，是一个无向简单图，定点和边关联
2. 最低支持minSup
输出(所有的频繁子图)
1. 如果子图至少是minSup*|D|的子图，则该子图是频繁的。或#minSup)D中的不同交易。
2. 每个子图都已连接。

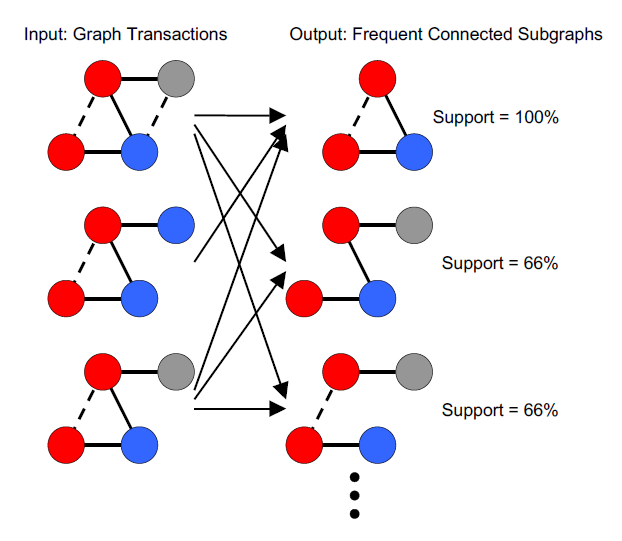
4.9.2. 先验式算法:FSG算法

Candidate generation：要确定两个候选候选对象，我们需要检查图同构。
Candidate pruning：要检查向下闭合特性，我们需要图同构。
Frequency counting：子图同构，用于检查频繁子图的包含性。

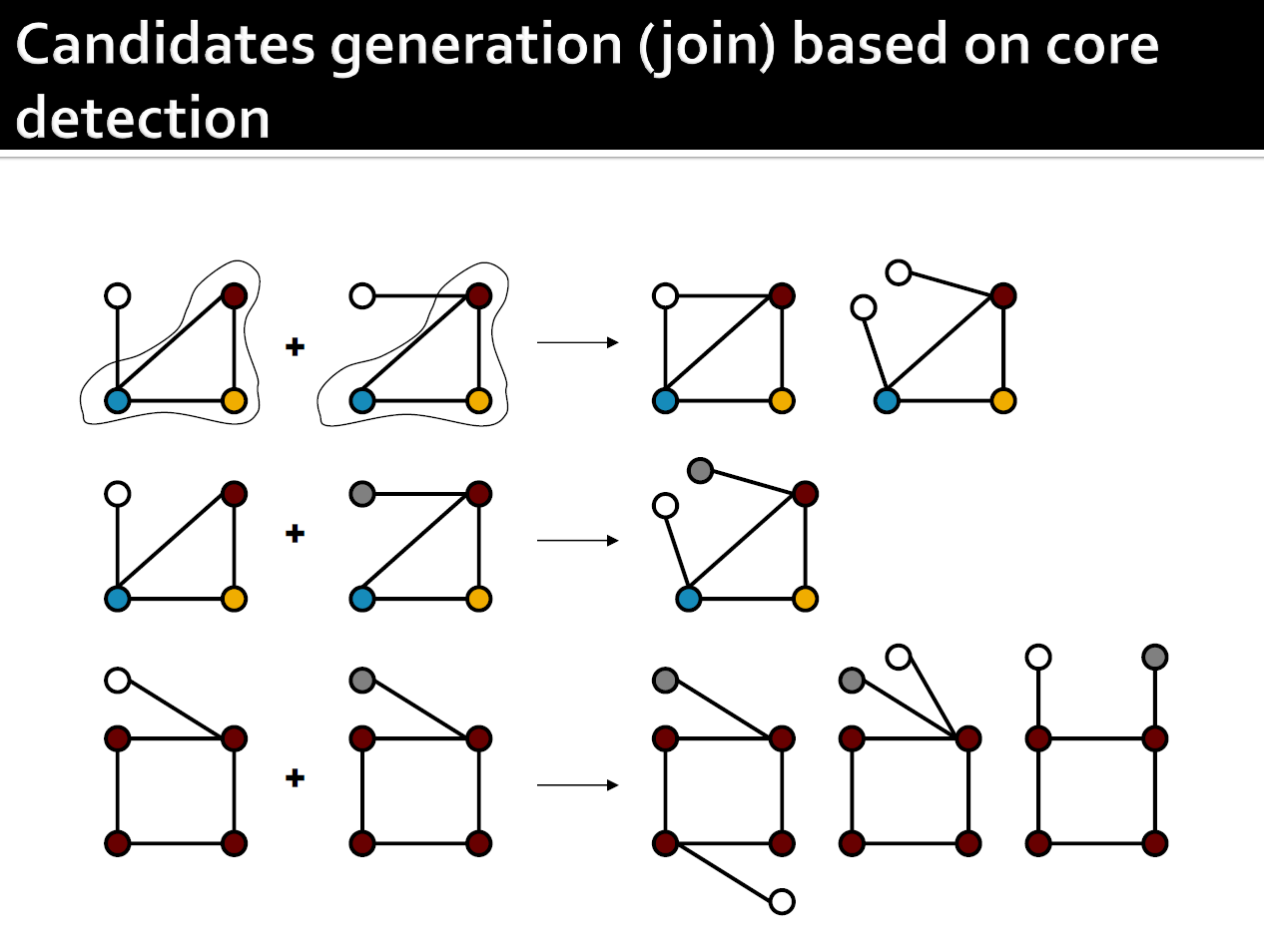
4.9.2.1. Candidate generation

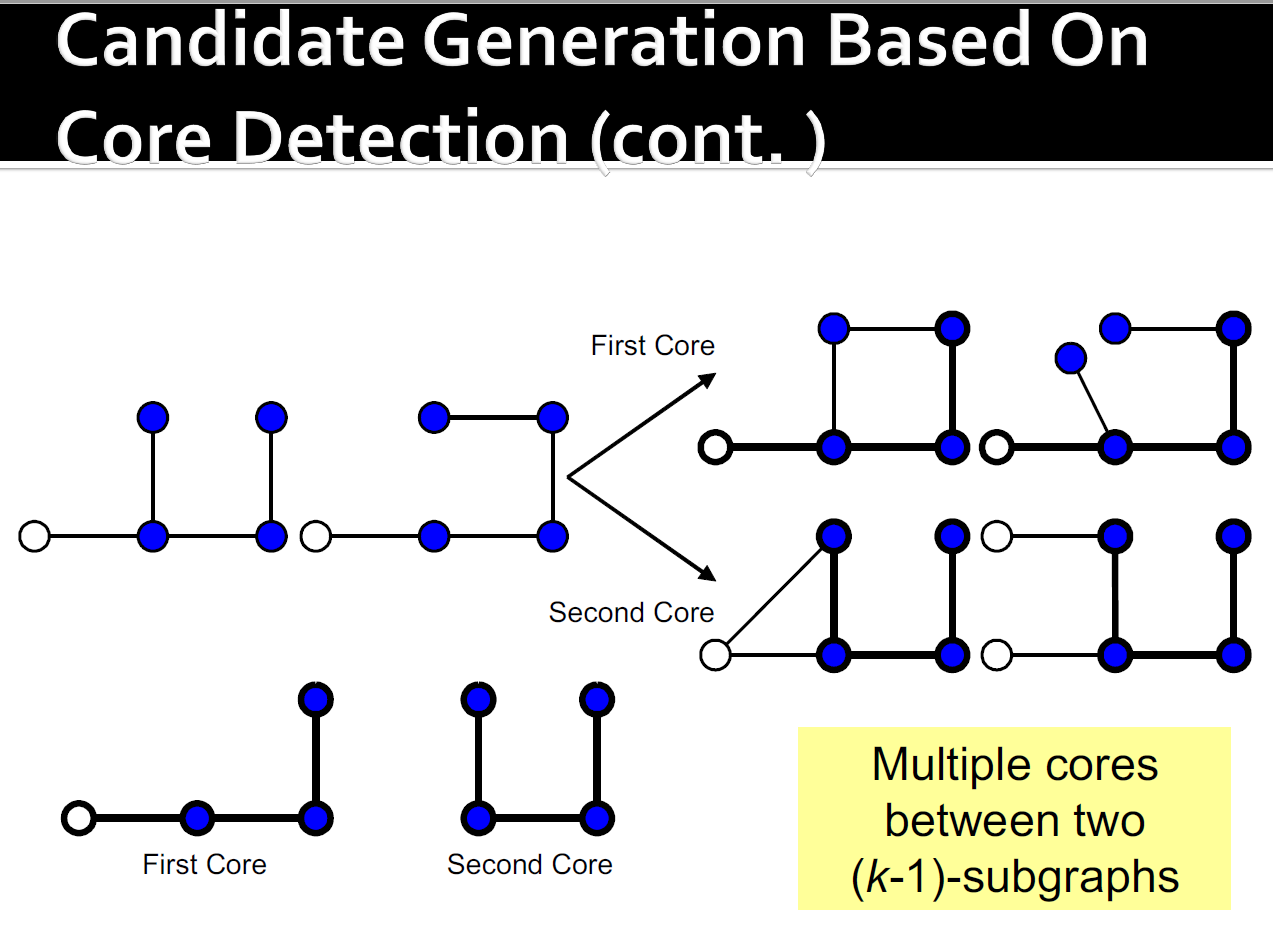
4.9.2.2. Candidate pruning：向下封闭属性

每个(k-1)个子图必须频繁出现。
对于给定k个候选的所有(k-1)个子图，检查向下闭合性是否成立

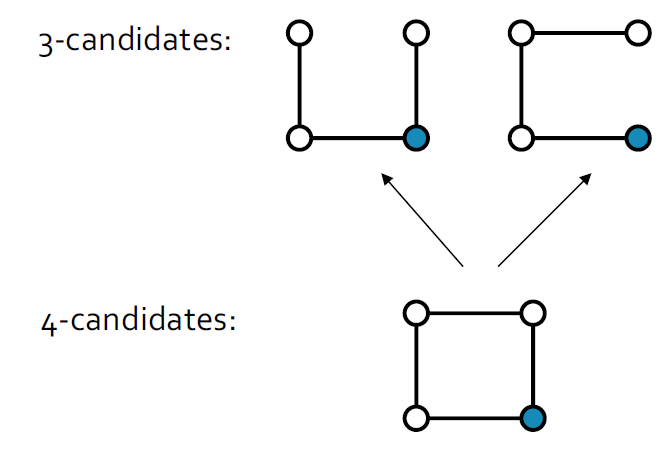
4.9.2.3. Frequency counting

4.9.2.4. 计算挑战

图上面的简单的计算会变得复杂并且高代价
Candidate generation
1. 为了确定我们是否可以加入两个候选者，我们需要执行子图同构来确定它们是否具有共同的子图。
2. 没有明显的方法可以减少我们生成同一子图的次数。
3. 需要执行图同构以进行冗余检查。
4. 两个频繁子图的联接可以导致多个候选子图。
Candidate pruning：要检查向下封闭性，我们需要子图同构。
Frequency counting：子图同构，用于检查频繁子图的包含性
FSG计算效率的关键：
1. 使用高效的算法来确定图形的规范标签，并使用这些"字符串"执行身份检查(字符串的简单比较！)。
2. 使用复杂的候选生成算法，可减少每个候选生成的次数。
3. 使用基于增强TID列表的方法来加快频率计数。

4.9.2.5. FSG：基于邻接矩阵的图规范化表示

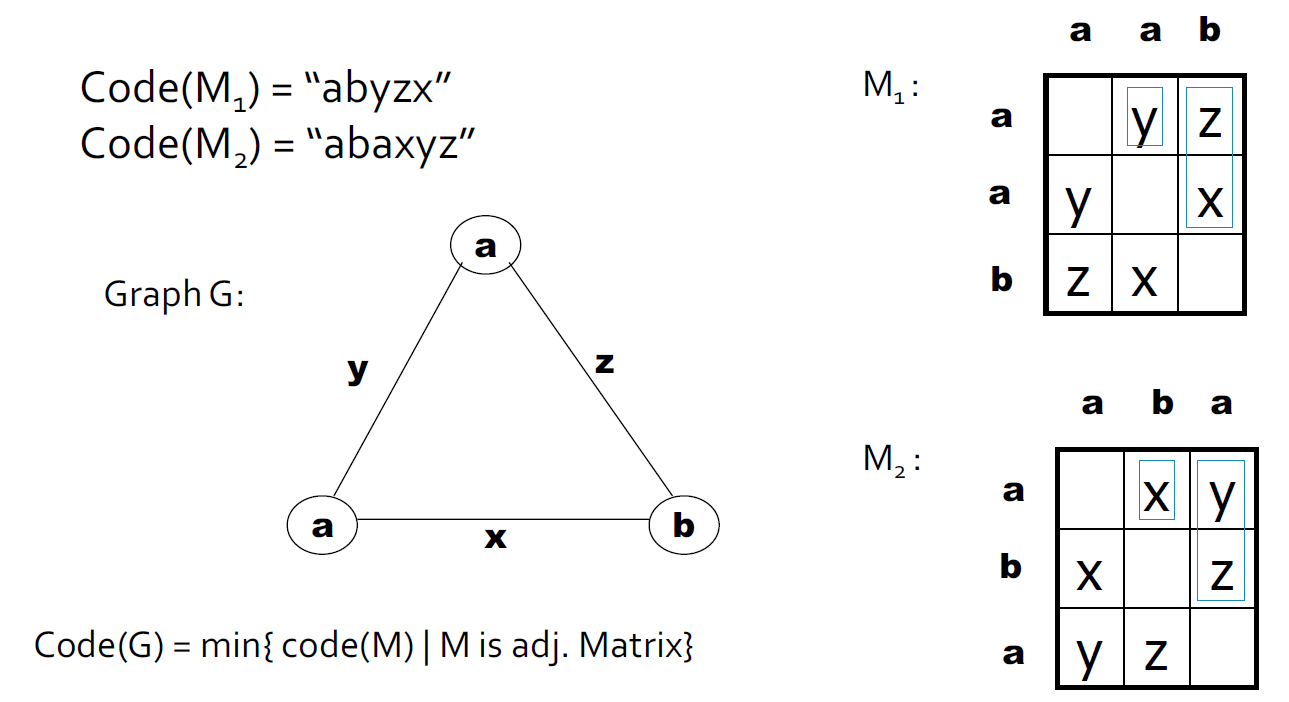
4.9.2.6. 规范化标记

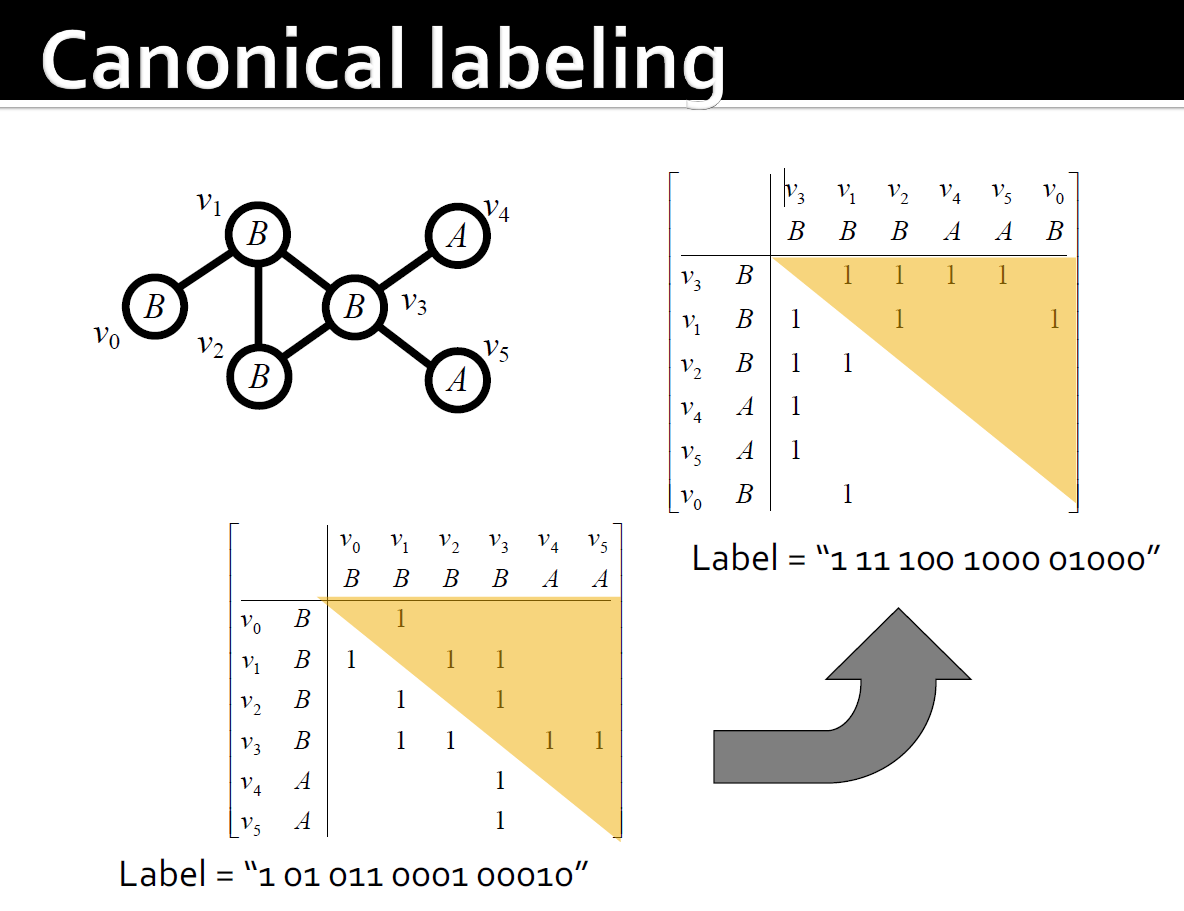
4.9.2.7. FSG：找到规范化标记

这个问题和图同构一样复杂，但是FSG建议使用一些启发式方法来加速它
如：
1. 顶点不变式(例如度)
2. 邻居列表
3. 迭代分区

4.9.2.8. 另一种FSG启发式算法：Frequency counting

4.9.2.9. 拓扑是不充分的

由物理域产生的图具有很强的几何性质，数据挖掘算法必须考虑这种几何形状。
几何图，顶点具有与之关联的物理2D和3D坐标。

4.9.3. gFSG:FSG的Geometric扩展

与FSG相同的输入和相同的输出：查找频繁的几何连接子图
(子)图同构的几何版本
1. 顶点的映射可以是平移，旋转和/或缩放不变的。
2. 只要坐标在r的公差半径内，坐标的匹配就可能不精确。R容忍的几何同构。

4.9.4. DFS方法:gSpan

4.9.4.1. 定义查询树空间(TSS，Tree Search Space)

数据集查询空间(前缀树)

4.9.4.1.1. TSS的驱动

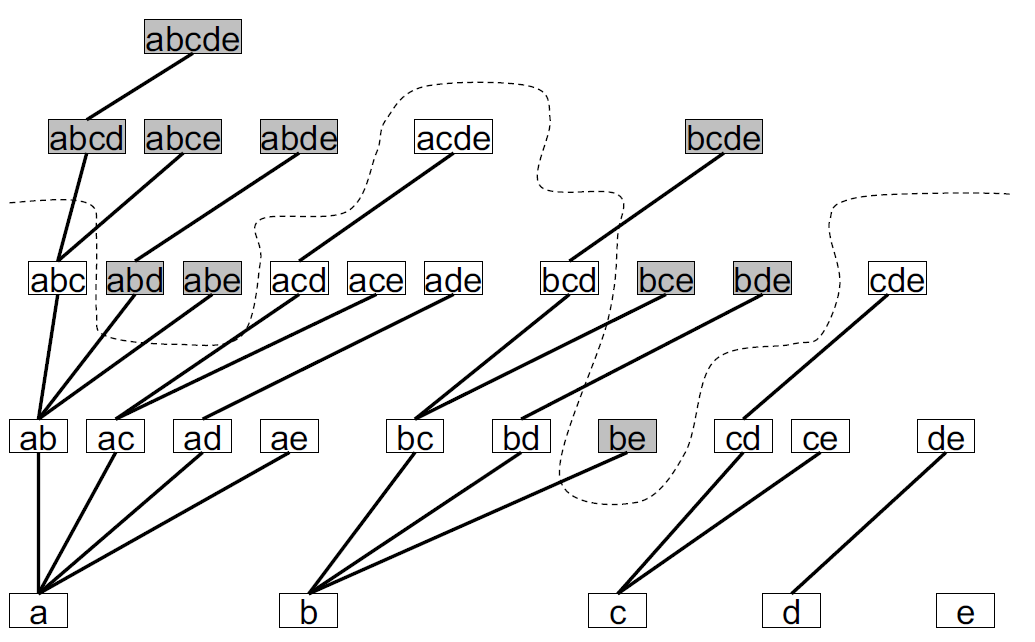
项集的规范表示是通过对项的完整顺序获得的。
每个可能的项目集在TSS中仅出现一次：没有重复或遗漏。
树搜索空间的属性
1. 对于每个k标签，其父对象是给定k标签的k-1前缀
2. 兄弟姐妹之间的关系按字典顺序升序。

4.9.4.1.2. DFS 编码表示

将每个图形(二维)映射到顺序的DFS代码(一维)。
按词典顺序对代码进行排序。
根据字典顺序构造TSS。

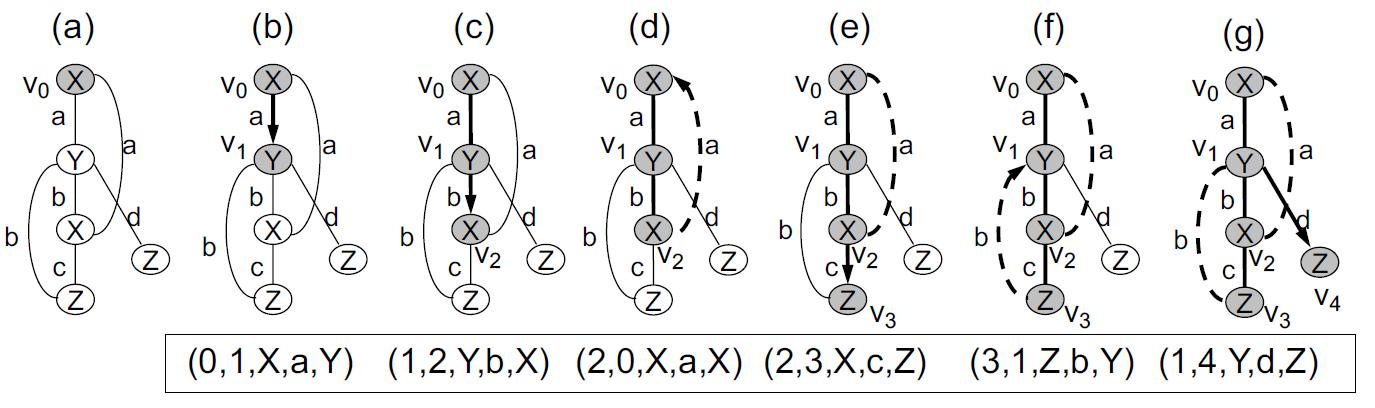
4.9.4.1.3. DFS编码过程

给定图G，针对图G上的每个深度优先搜索，构造相应的DFS代码。

4.9.4.1.4. 简单图与DFS编码示例

4.9.4.1.5. 最小化DFS编码

最小DFS代码min(G)(按DFS词典顺序)是图G的规范表示。
当且仅当以下条件时，图A和B是同构的：min(A)= min(B)

4.9.4.1.6. DFS编码数-父子关系

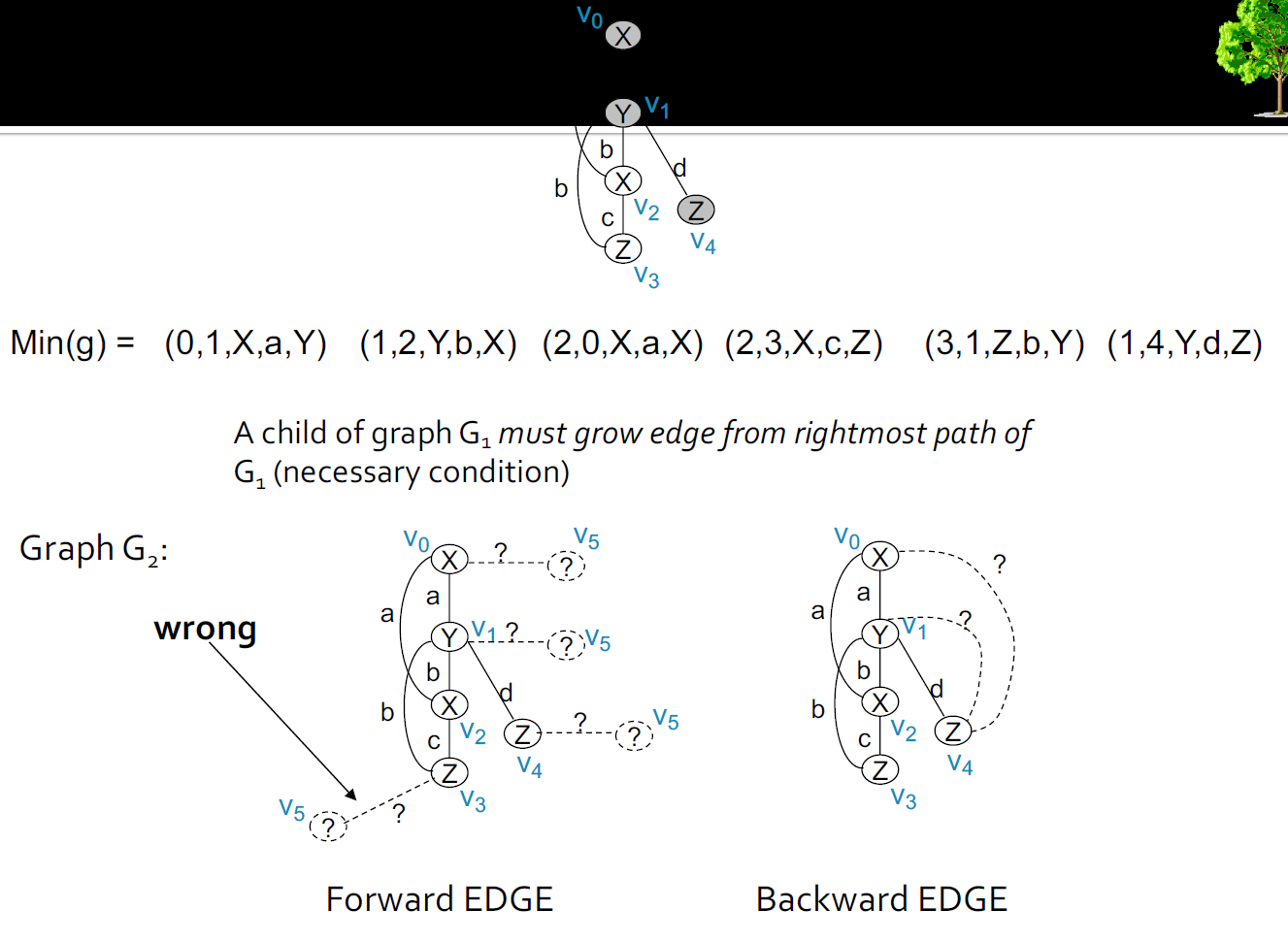
如果 $\min(G_1)= {a_0，a_1，...，a_n}$ $min (G_{1}) = a_{0} ， a_{1} ， . . . ， a_{n}$ 和 $\min(G_2)= {a_0，a_1，...，a_n，b}$ $min (G_{2}) = a_{0} ， a_{1} ， . . . ， a_{n} ， b$
1. G1是G2的父级
2. G2是G1的子代
有效的DFS代码要求b从最右边路径上的顶点开始增长(DFS搜索中的继承属性)

4.9.4.1.7. 搜索空间:DFS编码数

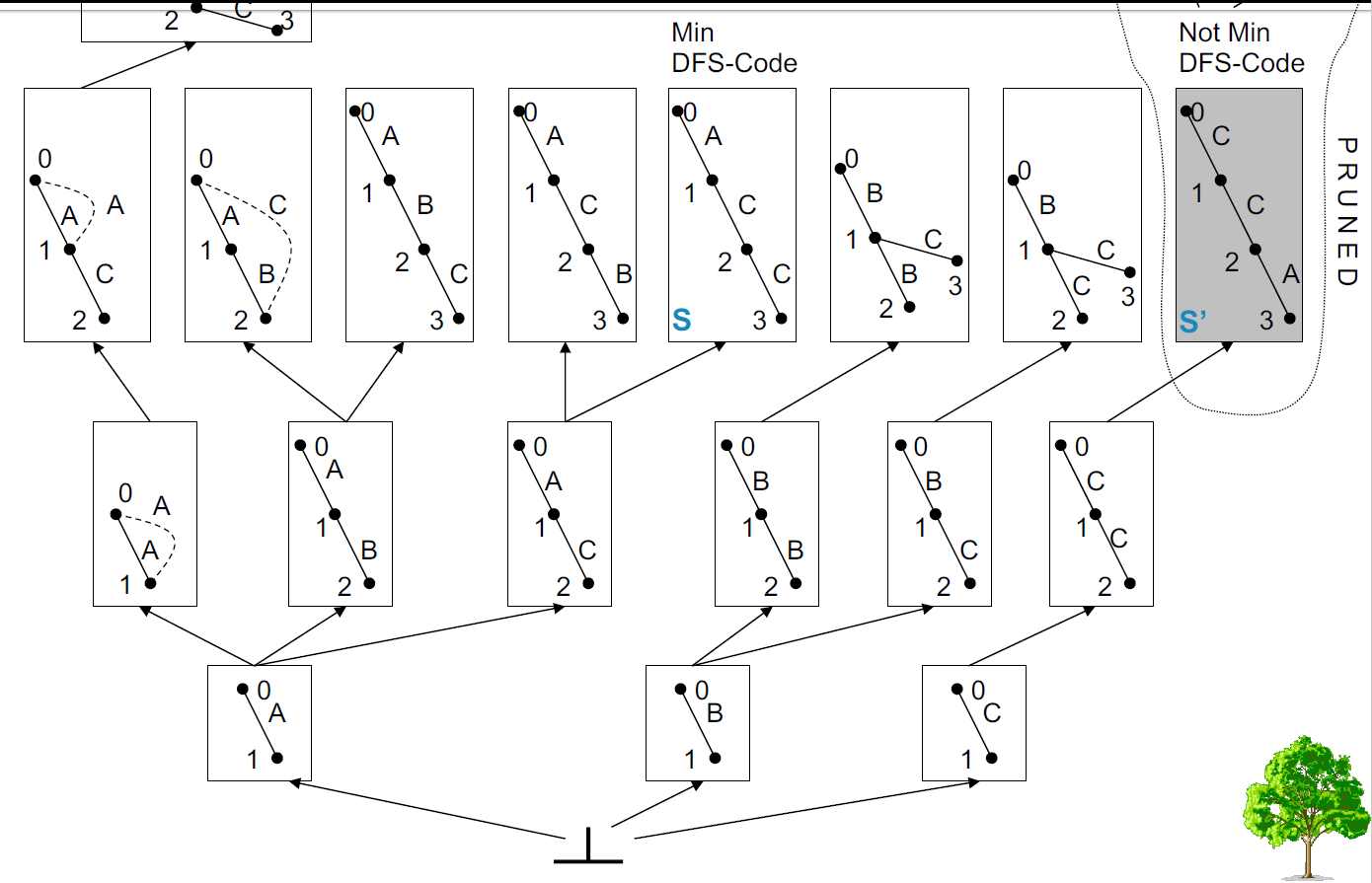
将DFS代码节点组织为父子节点。
兄弟节点按照DFS字典顺序升序组织。
按序遍历遵循DFS字典顺序！

4.9.4.1.8. 树剪枝

稀疏节点的所有后代也是稀疏的。
非最小DFS代码的所有后代也不是最小DFS代码。

4.9.4.2. gSpan使用TSS查找频繁图

4.9.4.2.1. gSpan内容

4.9.4.2.2. 示例

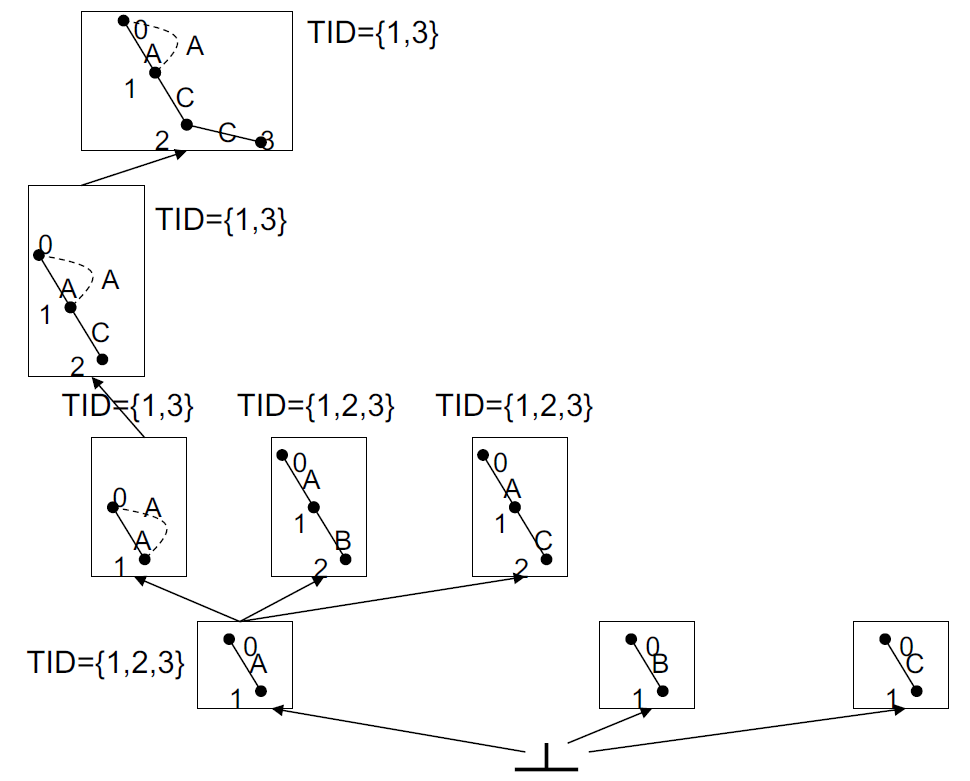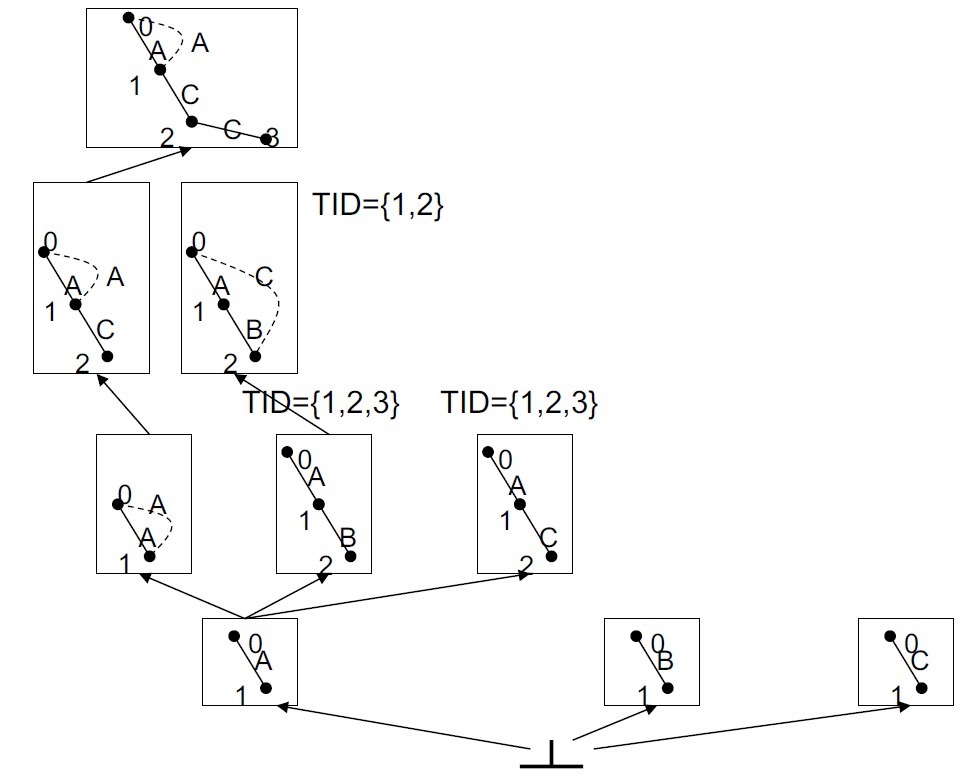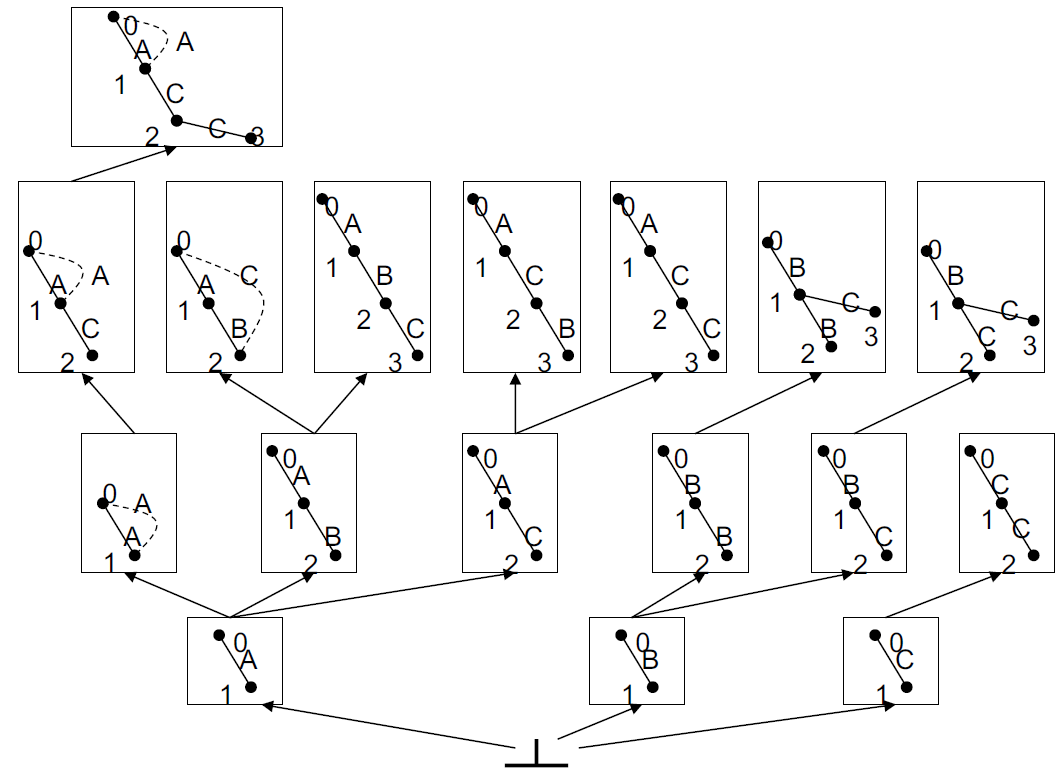4.9.4.3. gSpan算法表现

在合成数据集上，它比FSG快6-10倍。
在化合物数据集上，它快15到100倍！
但这与FSG的旧版本相比！

4.9.5. 贪婪算法:Subdue

一种贪婪算法，用于查找一些最普遍的子图。
此方法不完整，即虽然可以快速执行，但可能无法获得所有频繁的子图。
它发现可压缩原始数据并表示数据中结构概念的子结构。
基于波束搜索与BFS一样，它逐级进行。但是，与BFS不同，波束搜索仅通过每个级别的最佳W节点向下移动。其他节点将被忽略。

4.9.5.1. 图模式探索问题

如果图是频繁的，则其所有子图都是频繁的：先验属性
n边频繁图可能有2n个子图
在AIDS抗病毒筛选数据集中被确认具有活性的422种化合物中，如果最低支持为5％，则有1,000,000个频繁的图形模式

4.9.5.2. 第一步:为每个唯一的顶点标签创建子结构

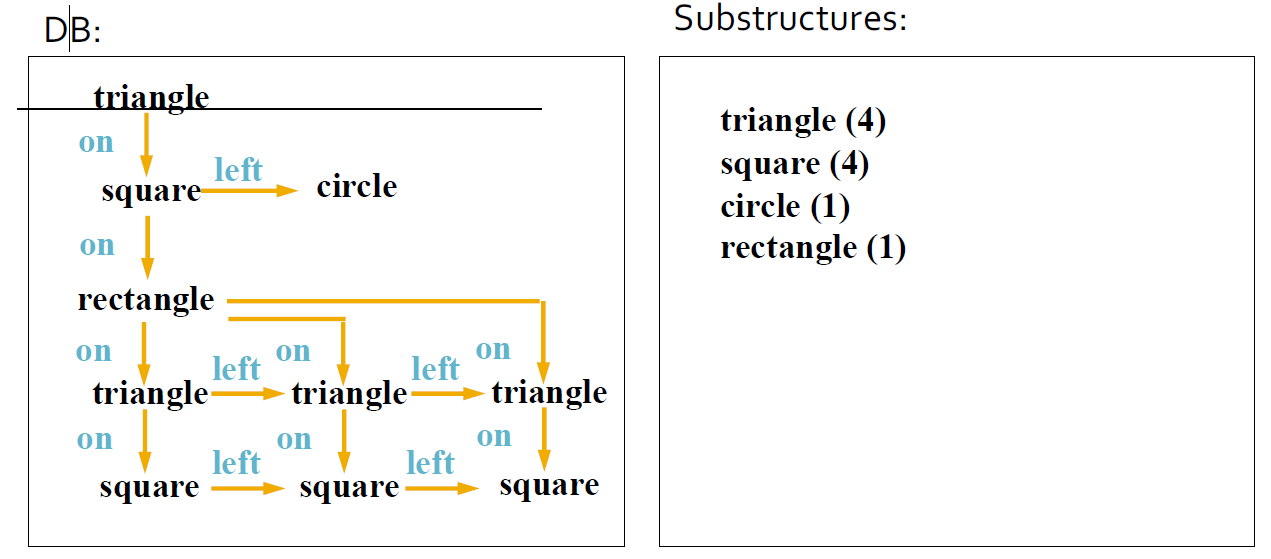
4.9.5.3. 第二步:通过边或边和相邻顶点扩展最佳子结构

4.9.5.4. 第三步：仅将最佳子结构保留在队列中(由光束宽度指定)

4.9.5.5. 第四步：在队列为空或发现的子结构数大于或等于指定的限制时终止。

4.9.5.6. 第五步：压缩图并重复以生成层次描述。

4.10. Single graph setting问题

现有的大多数算法都使用Transaction setting方法。
也就是说，如果某个模式甚至多次出现在Transaction中，则将其计为1(FSG，gSPAN)。
如果整个数据库是单个图形怎么办？这称为单图设置。
我们需要一个不同的支持定义！

4.10.1. 单个图设定

输入(D, minSup)
1. 一个简单图D(比如网络或者存储在XML中的BDLP)
2. 最低支持minSup
输出(所有的频繁子图)
1. 如果子图中在D中出现的次数大于允许的支持度量(满足向下封闭性的度量)，则该子图是频繁出现的。

4.10.2. 单个图设计:动机

输入通常是一个大图。
示例：
1. 网页或网页的一部分。
2. 社交网络(例如，通过BGU通过电子邮件进行通信的用户网络)。
3. 大型XML数据库，例如DBLP或Movies数据库。
挖掘大型图形数据库非常有用。

4.10.3. 支持的问题

如果对于任何模式P和任何子模式QÌP，P的支持不大于Q的支持，则允许采取支持措施。
问题：图案出现的数量不好！

4.10.4. 支持的问题

数据库图D中的模式P的实例图是这样的图：其节点是D中的模式实例，并且当相应的实例共享边时，它们通过边连接。
实例图上的操作
1. clique收缩：用单个节点c替换组C。只有与C的每个节点相邻的节点才可以与c相邻。
2. 节点扩展：用新的子图替换节点v，该子图的节点可能与相邻于v的节点相邻或不相邻。
3. 节点添加：向图中添加一个新节点，并在新节点和旧节点之间添加任意边。
4. 边去除：去除边

4.10.5. 主要的结果

定理。当且仅当在团簇收缩，节点扩展，节点添加和边缘去除下每个模式P的实例图上不减少时，支持度量S才是允许的支持度量。
支持度量示例

MIS = \frac{实例图的最大独立设置大小}{数据库图中的边数}

4.10.6. 路径挖掘算法(Vanetik，Gudes，Shimony)

目标：查找数据库图的所有频繁连接的子图。
基本方法：Apriori或BFS。
1. 基本构建块是路径而不是边。
2. 这是可行的，因为任何图都可以分解为边不相交的路径。
结果：算法收敛更快。

4.10.6.1. 基于路径的挖掘算法

该算法使用路径作为模式构建的基本构建块。
它从单路径图开始，然后将它们组合为2、3等路径图。
组合技术不使用图形运算，易于实现。
图的路径数以线性时间计算：奇数度顶点的数量除以2。
给定最小路径覆盖P，给定一条路径的删除将创建一个具有最小路径覆盖大小|P| -1的图形。
P中至少存在两条路径，将其删除会使图形保持连接状态。

4.10.6.2. 超过一条边覆盖的图

根据节点标签和节点度定义每个路径的描述符。
使用描述符中的字典顺序在路径之间进行比较。
一张图可以具有多个最小路径覆盖。
我们只使用与字典顺序相关的最小的路径覆盖。
从词典上最小的路径封面中删除路径，使封面在词典上最小。

4.10.6.3. 路径描述符示例

4.10.6.4. 路径挖掘算法

阶段1：找出所有常见的1-路径图。
阶段2：通过"加入"频繁的1-路径图找到所有频繁的2-路径图。
阶段3：通过"联接"成对的(k-1)路径图，找到所有频繁的k路径图， $k \geq 3$ 。
主要挑战："加入"必须确保算法的健全性和完整性。

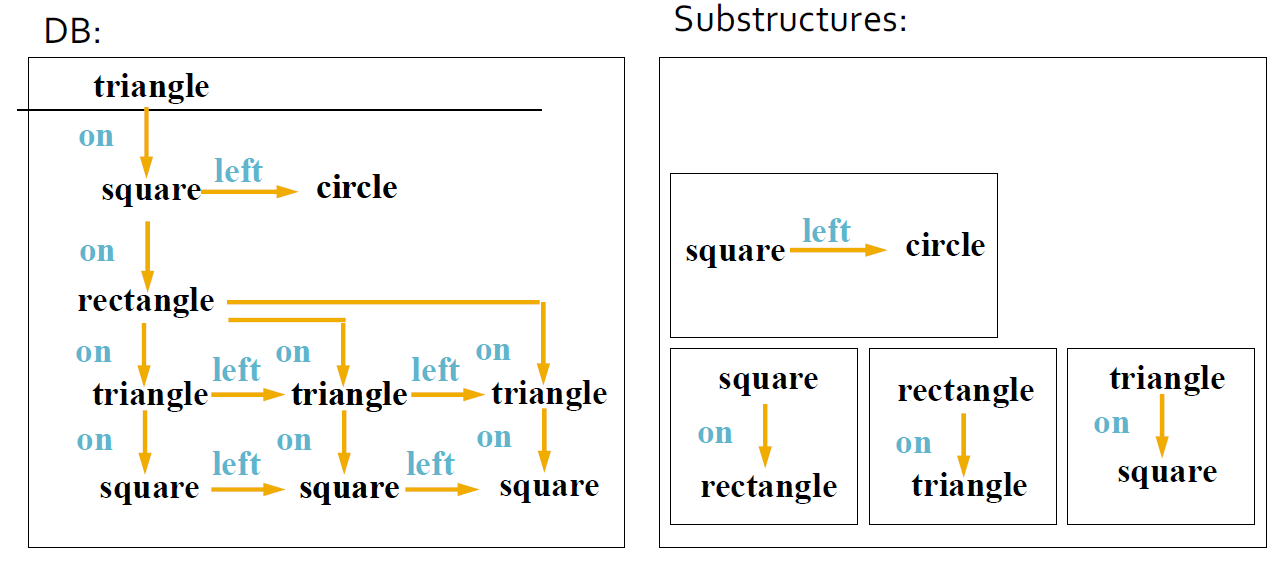
4.10.6.5. 图形作为路径的集合：表表示

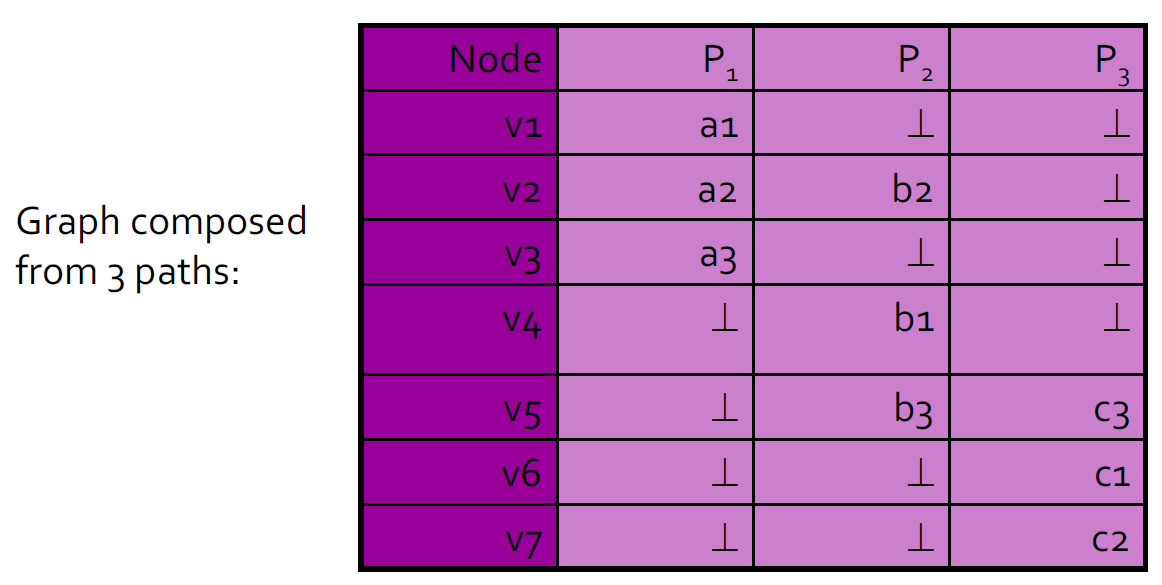
4.10.6.6. 从表中删除路径

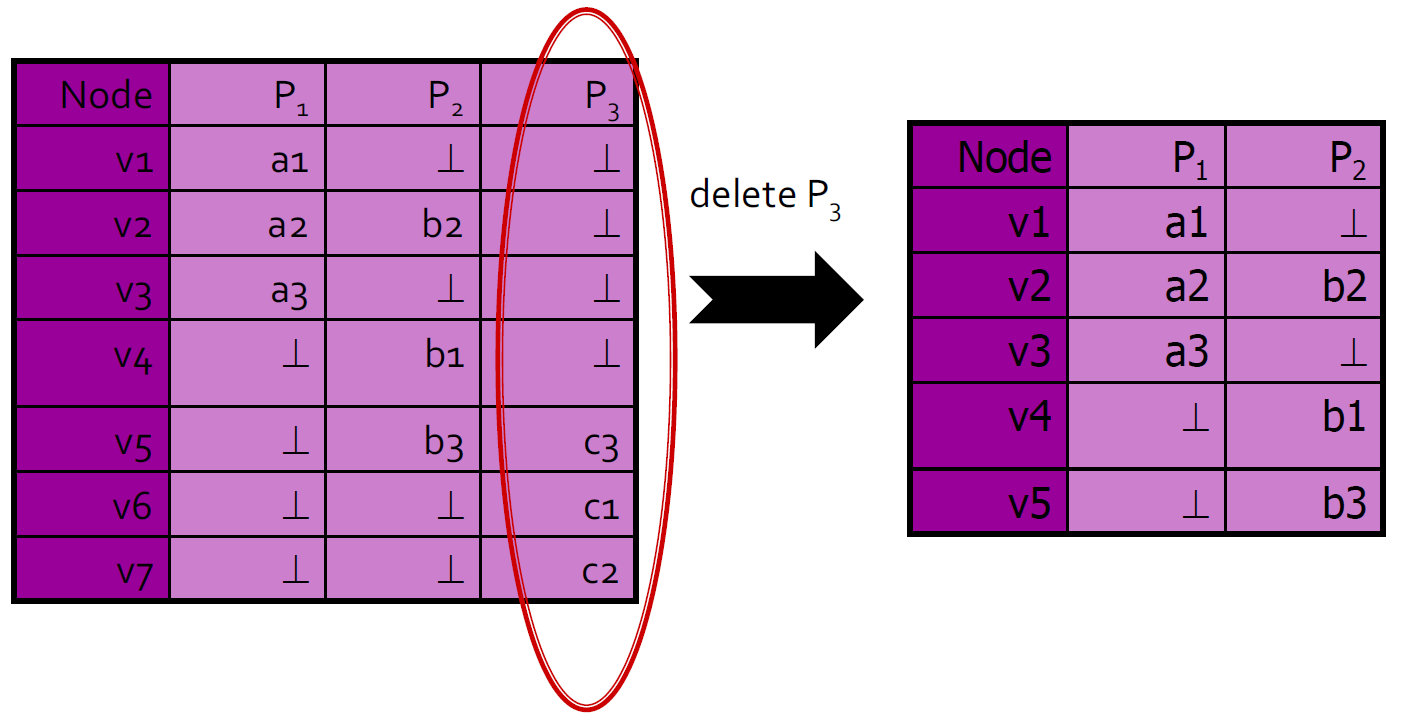
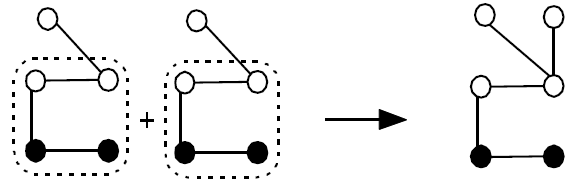
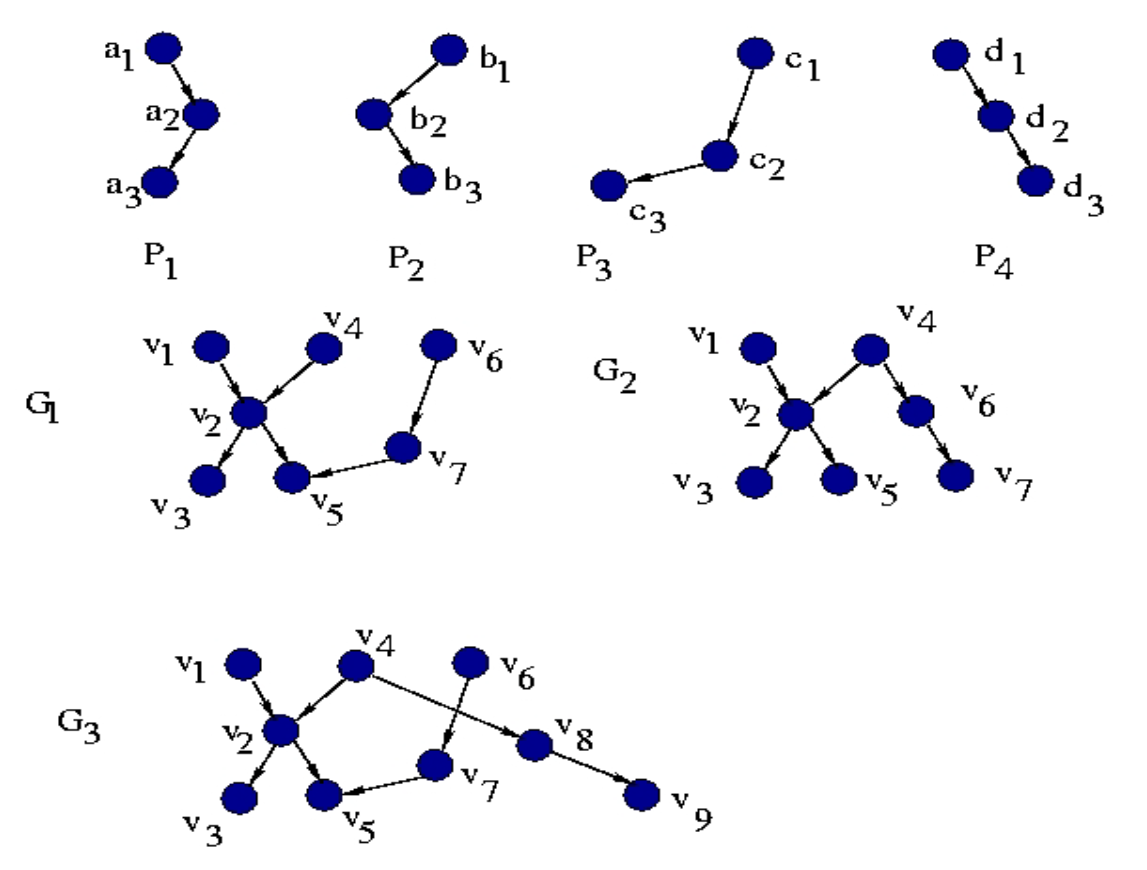
4.10.6.7. 用通用路径联接图：求和运算

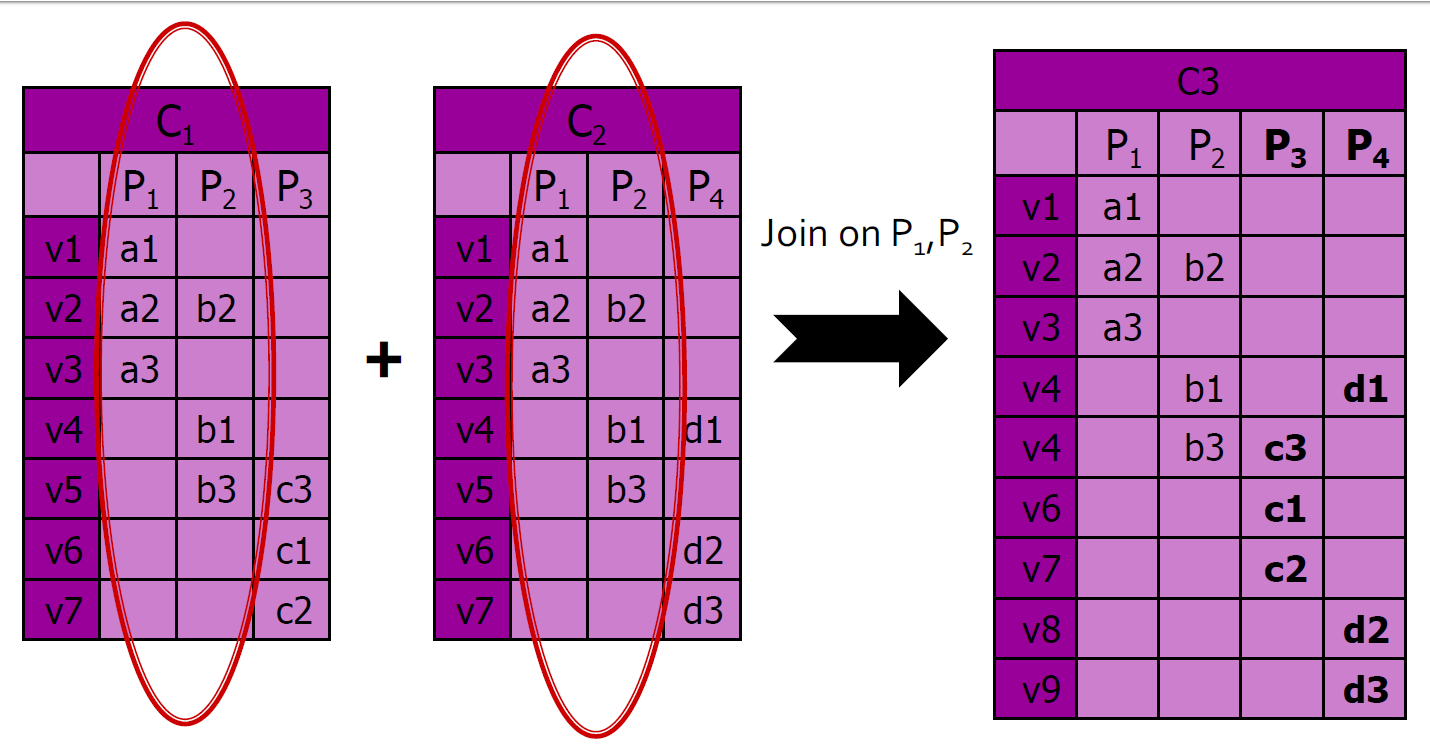
求和运算：在图形上的外观

4.10.6.8. 总和是不够的：拼接操作

我们需要在路径 $P_1,...,P_n$ 上构造一个频繁的n路径图G。
我们有两个频繁的(n-1)个路径图，路径 $P_1,...,P_{n-1}$ 上的G1和路径 $P_2,...,P_n$ 上的G2。
G1和G2的总和将为我们在路径 $P_1,...,P_n$ 上提供n路径图G’。
如果P1和Pn没有仅属于它们的公共节点，则G’= G。
如果G频繁出现，则包含P1和Pn的精确2-路径图H完全与G中出现的一样。
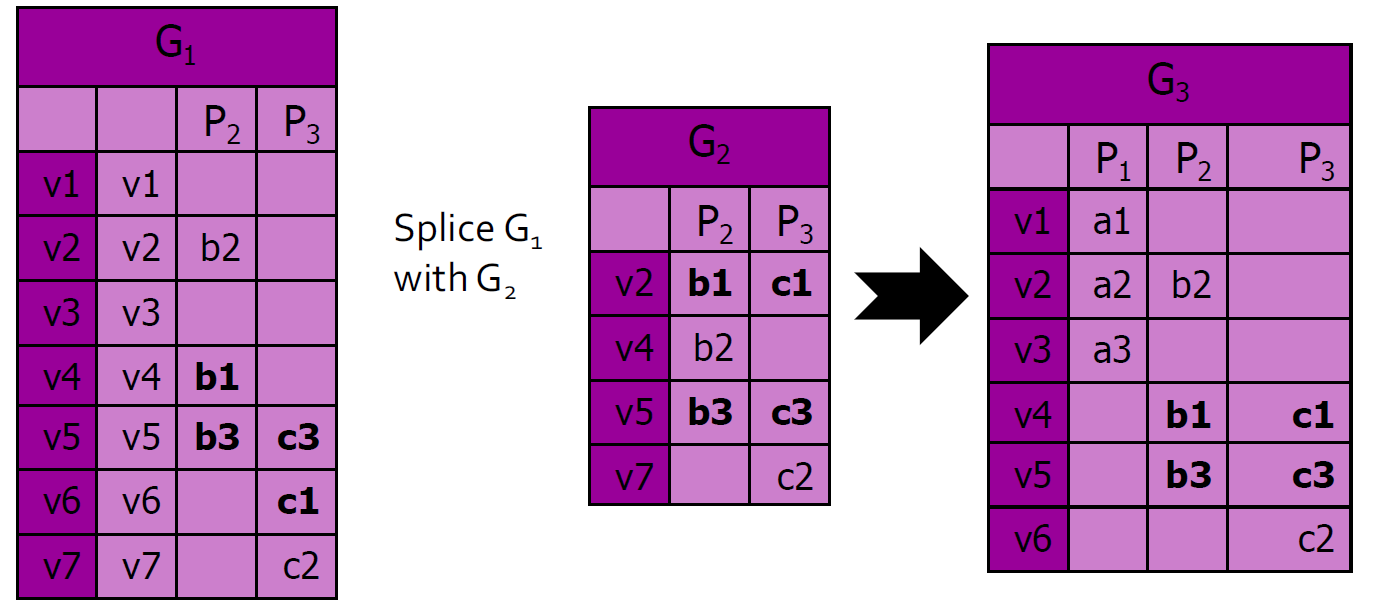
让我们根据H加入G’中P1和Pn的节点。这是拼接操作！

拼接操作例子

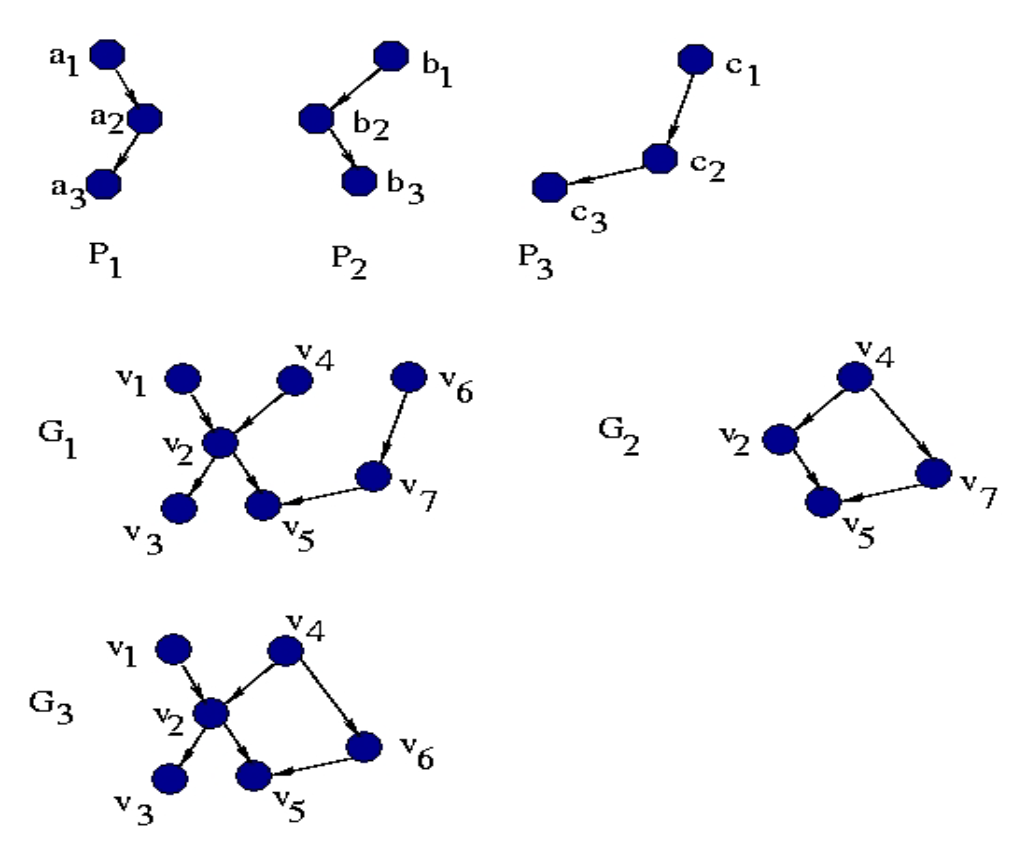
拼接操作：在图形上的外观

4.10.6.9. 标记图：我们注意标记

4.10.6.10. 路径挖掘算法例子

查找所有常见的边。
通过一次添加一条边找到频繁的路径(并非所有节点都适合！)
通过穷举查找所有频繁的2路径图。
设置k = 2。
虽然存在频繁的k路径图
1. 在适用的情况下，对成对的频繁k路径图执行求和运算。
2. 对生成的(k + 1)个路径候选者执行拼接操作，以获得其他(k + 1)个路径候选者。
3. 计算对(k + 1)个路径候选者的支持。
4. 消除不经常出现的候选人，并设置k：= k + 1。
5. 转到5。

4.10.7. 复杂性

指数-频繁模式的数量可以指数，数据库大小(如任何Apriori算法)
艰巨的任务：(NP hard)
1. 支持的计算包括：在数据库中查找频繁模式的所有实例。(子图同构)
2. 计算实例图的MIS(最大独立集合大小)。
相对简单的任务：
1. 候选集生成：上一次迭代中频繁集大小的多项式，
2. 消除同构候选模式：图同构计算在最坏的情况下取决于模式的大小，而不是数据库的指数。

4.10.8. 简单图设置的补充方法

BFS Approach：hSiGram
DFS Approach：vSiGram
两者都使用MIS测度的近似值

4.11. 封闭频繁图

频繁图G关闭：如果不存在与G具有相同支持的G的上标
如果某些G的子图具有相同的支持
1. 不必输出这些子图
2. 非封闭图
无损压缩：仍确保挖掘结果完整

4.12. 图搜索

查询图数据库：给定图数据库和查询图，找到包含该查询图的所有图

4.13. 可扩展性

天真的解决方案
1. 顺序扫描(磁盘I / O)
2. 子图同构测试(NP完全)
问题：可伸缩性是一个大问题
需要索引机制

4.14. 索引策略

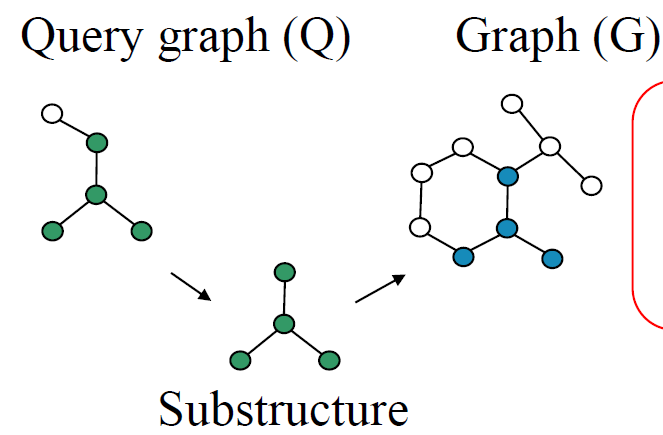
如果图G包含查询图Q，则G应该包含Q的任何子结构
备注：将查询图的子结构索引到不包含这些子结构的修剪图

4.14.1. 索引框架

处理图查询的两个步骤
步骤1.索引构建，枚举图数据库中的结构，在结构和图之间建立反向索引
步骤2.查询处理
1. 列举查询图中的结构
2. 计算包含这些结构的候选图
3. 通过执行子图同构测试来修剪错误肯定答案

4.14.2. 为什么结果频繁

我们无法索引(甚至搜索)所有子结构
大型结构很可能会被其子结构索引
增加规模的支持门槛

4.14.3. 结构相似查询

4.14.4. 子结构相似度度量

基于特征的相似性度量
每个图都表示为一个特征向量

X = {x_1，x_2，...，x_n}

相似性是由它们对应的距离定义的向量
优点
1. 易于索引
2. 快速
3. 粗略的措施

4.14.5. 一些更直接的方法

方法1：直接计算数据库中的图和查询图之间的相似度
1. 顺序扫描
2. 子图相似度计算
方法2：根据原始查询图形成一组子图查询，并使用精确的子图搜索。代价高昂：如果我们允许在20条边的查询图中遗漏3条边，则可能会生成1,140个子图

4.14.6. 索引:精确和模糊查询

精确搜寻
1. 使用频繁模式作为索引功能
2. 根据其选择性在数据库空间中选择特征
3. 建立索引
近似搜索
1. 难以建立涵盖相似子图的索引
2. 数据库中子图的爆炸数量
3. 想法：
  1. 保持索引结构
  2. 在查询空间中选择要素

4.15. 图分类问题

4.15.1. 基于子结构的图分类问题

基本思路
1. 提取图子结构， $F = {g_1, ..., g_n}$
2. 用特征向量 $X = {x_1, ..., x_n}$ 表示图， $x_1$ 是 $g_i$ 在图中出现的次数。
3. 建立分类模型
不同的功能和代表性的工作
1. 指纹
2. Maccs键
3. 树和循环模式[Horvath等]
4. 最小对比度子图[Ting和Bailey]
5. 频繁的子图[Deshpande等；刘等]
6. Graph片段[Wale和Karypis]

4.15.2. 直接挖掘判别模式

避免挖掘整个模式
1. Harmony [Wang和Karypis]
2. DDPMine [Cheng等]
3. LEAP [Yan等]
4. MbT [Fan等]
找到最有区别的模式
1. 搜索问题
2. 优化问题
扩展
1. 挖掘前k个判别模式
2. 挖掘近似/加权判别模式

4.15.3. 图的核函数

驱动：
1. 基于内核的学习方法不需要访问数据点
2. 它们依赖于数据点之间的内核功能
3. 可以应用于任何复杂的结构，前提是您可以在它们上定义内核函数
基本思路：
1. 将每个图形映射到一些重要的模式
2. 在相应的模式集上定义内核

4.15.4. 基于核函数的分类

随机漫步
1. 基本思想：计算两个图标之间匹配的随机游动
2. 边缘核函数

K(G_1, G_2) = \sum\limits_{h_1}\sum\limits_{h_2}p(h_1)p(h_2)K_L(l(h_1), l(h_2))

$h_1$ 和 $h_2$ 是图 $G_1$ 和 $G_2$ 中的路径
$p(h_1)$ 和 $p(h_2)$ 是路径上的可能性分布
$K_L(l(h_1), l(h_2))$ 是路径间的核函数

K_L(l_1,l_2)=\begin{cases} 1 & if\ l1 = l2 \\ 2 & otherwise \end{cases}

4.15.5. 图分类的Boosting方法

决策树桩

简单的分类器，其中的最终决定由单个特征决定
规则就是元组 $<t, y>$
如果分子包含子结构y，则将其分类为t。
Gain

h_{<t, y>}(x) = \begin{cases} y & if t \subseteq{x} \\ -y & otherwise \\ \end{cases}

应用提升

\begin{matrix} gain(<t, y>) = \sum\limits_{i=1}\limits^n y_ih_{<t, y>}(x_i) \\ gain(<t, y>) = \sum\limits_{i=1}\limits^n y_ih_{<t, y>}(x_i) \end{matrix}

4.16. 图聚类问题

4.16.1. 图压缩

提取公共子图并通过将这些子图压缩为节点来简化图

4.16.2. 图/网络聚类问题

由数据元素的相互关系组成的网络通常具有基础结构。由于关系很复杂，因此很难发现这些结构:如何弄清楚结构？
有了有关谁与谁联系的简单信息，就可以确定具有共同兴趣或特殊关系的个人群体吗？例如，家庭，集团，恐怖分子牢房…

4.16.3. 网络的例子

多少个集群？
他们应该是多大？
最好的分区是什么？
是否应将某些观点分开？

4.16.4. 社交网络模型

紧密的社会群体或集团中的人认识许多相同的人，不论小组大小
成为枢纽的人认识不同组中的许多人，但不属于单个组，例如，政治人物跨多个团体
离群的人生活在社会的边缘，例如，隐士认识的人很少，不属于任何群体

4.16.5. 顶点邻居

将G(v)定义为顶点的直接邻域，即个人认识的一群人

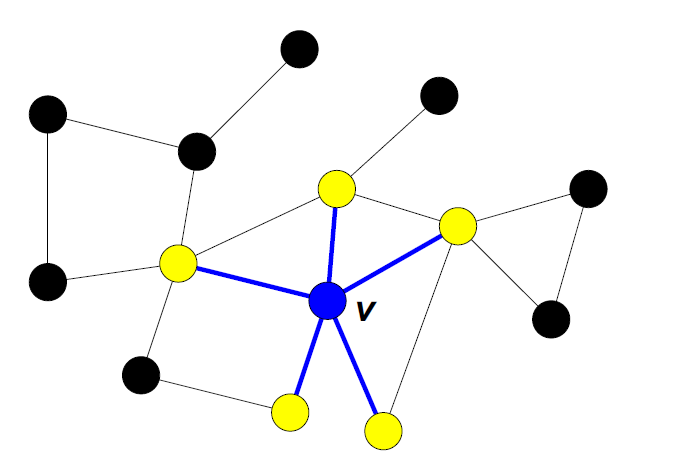
4.16.6. 结构相似性

所需的特征倾向于通过称为结构相似性的度量来捕获

\sigma(v, w) = \frac{|\Gamma(v) \cap \Gamma(w)|}{\sqrt{|\Gamma(v)||\Gamma(w)|}}

对于集团成员而言，结构相似性很大，而对于中心和离群点而言，结构相似性很小。

4.16.7. 社团

社区：它是由个人组成的，因此与组外的人相比，组内的人之间的互动更加频繁，在不同上下文中也称为组，群集，内聚子组，模块
社区检测：在网络中发现未明确授予个人组成员身份的组
为什么在社交媒体中使用社区？
1. 人类是社会的
2. 易于使用的社交媒体使人们能够以前所未有的方式扩展社交生活
3. 很难认识现实世界中的朋友，但更容易在网上找到志趣相投的朋友
4. 节点之间的交互可以帮助确定社区

4.16.8. 社交媒体的社团

社交媒体中的两种类型的群体
1. 显式群体：由用户订阅组成
2. 隐性群体：由社交互动隐式形成
一些社交媒体网站允许人们加入群组，是否有必要根据网络拓扑提取群组？
1. 并非所有站点都提供社区平台
2. 并非所有人都愿意努力加入团体
3. 组可以动态变
网络交互可提供有关用户之间关系的丰富信息
1. 可以补充其他类型的信息，例如用户资料
2. 帮助网络可视化和导航
3. 提供其他任务的基本信息，例如建议请注意，以上三点中的每一个都可以成为研究主题。

4.17. 总结

数据挖掘领域通过有效的DM算法证明了其在短生命周期内的实用性。
在数据库，化学与生物学，网络等领域有许多应用程序。
交易和单图设置都很重要
图挖掘是
1. 处理为挖掘图数据集而设计的有效算法。
2. 途中面临许多硬度问题。
3. 快速发展的领域，具有前所未有的发展潜力。
随着越来越多的信息存储在复杂的结构中，我们需要为图形数据挖掘开发一套新的算法。

5. 文档分类

多语言的替代表示
Web文档：基于图的模型

5.1. 基于图模型的网络文档

基本思路：
1. 每个唯一术语一个节点
2. 如果单词B紧跟单词A，则从A到B有一条边：在存在标点符号(句号，问号和感叹号)的情况下，两个单词之间未形成边线
3. 通过仅包含最常用的术语来限制图形大小
4. 节点和边缘标签的几种变体(请参阅下一张幻灯片)
预处理步骤
1. 停用词已删除
2. 合法化：同一术语的替代形式(单数/复数，过去/现在/将来时等)被合并为最常见的形式

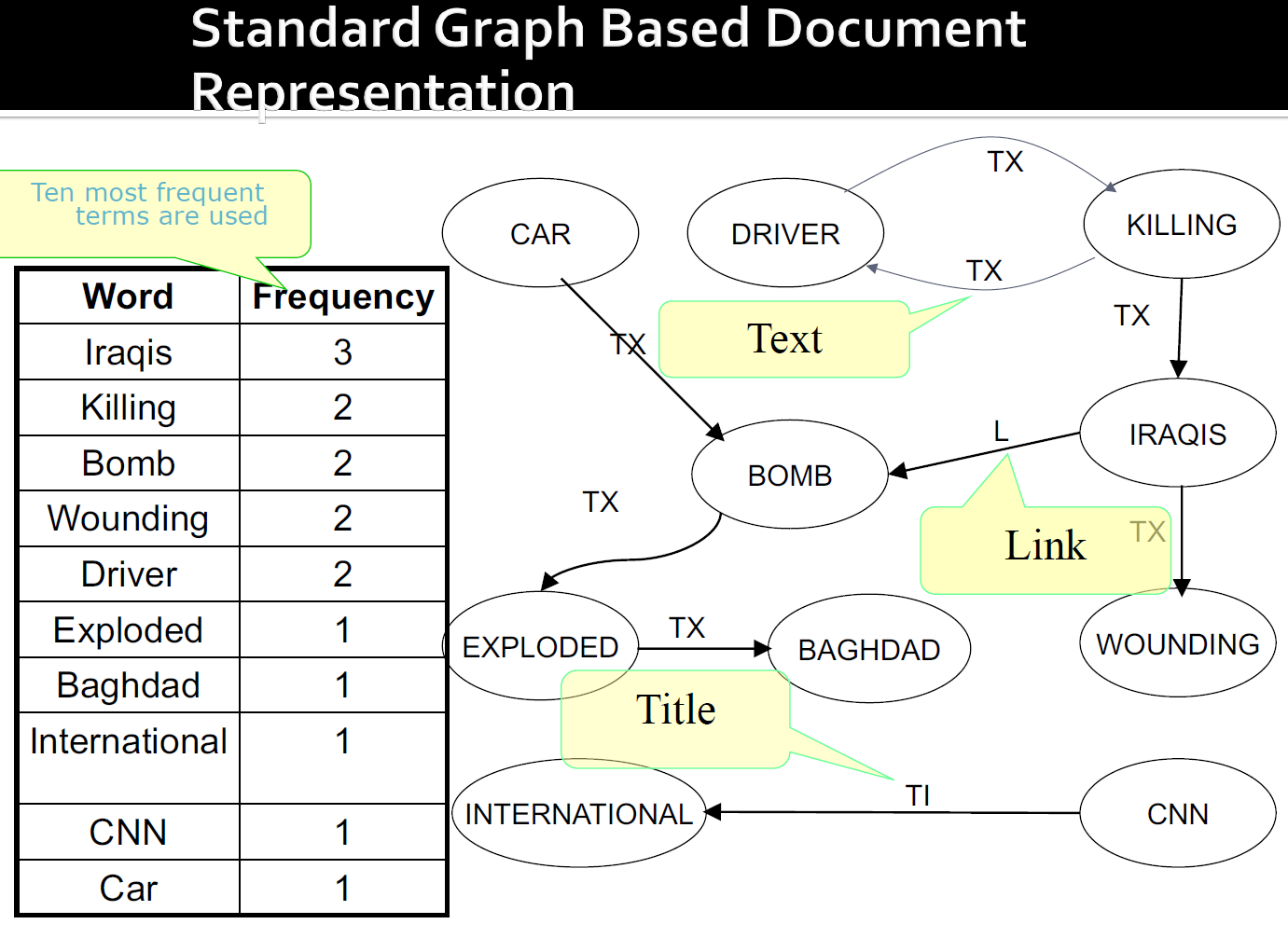
5.2. 标准化表示

边缘根据文档部分标记，单词彼此紧跟
1. 标题(TI)包含与文档标题和任何提供的关键字(元数据)有关的文本；
2. 链接(L)是出现在文档上可点击的超链接中的"锚文本"；
3. 文本(TX)包含文档中的任何可见文本(这包括锚文本，但不包括标题和关键字文本)

5.3. 使用图进行分类

基本思路：
1. 挖掘频繁的子图，称其为术语
2. 使用TFIDF为文档分配最具特色的术语
3. 使用聚类和K近邻分类

5.4. 子图挖掘

输入值
1. G –有向，唯一节点图的训练集
2. $CR_{min}$ :最低分类率
输出:与分类相关的子图集
流程：
1. 对于每个类，找到子图 $CR$ > $CR_{min}$
2. 将所有子图合并为一组
基本假设:与类别相关的子图在特定类别中比在其他类别中更常见

5.5. 计算分类率

子图分类率：

CR(g'_k(c_i)) = SCF(g'_k(c_i)) * ISF(g'_k(c_i))

$SCF(g'_k(c_i))$ :子图类别 $c_i$ 类中子图 $g'_k$ 的频率
$ISF(g'_k(c_i))$ :类别 $c_i$ 中子图 $g'_k$ 的逆子图频率
分类相关功能是最能解释特定类别的功能，该类别比其他所有类别更常见

2020-大数据分析

#课程笔记 #大数据分析 #社团网络

2020-大数据分析-Lecture11-图挖掘

https://spricoder.github.io/2020/11/01/2020-Big-data-analysis/2020-Big-data-analysis-Lecture11-%E5%9B%BE%E6%8C%96%E6%8E%98/

作者

SpriCoder

发布于

2020年11月1日

许可协议

2020-大数据分析-Lecture12-Spark与数据分析上一篇

2020-大数据分析-Lecture10-Graph DB 下一篇