2020-数据科学基础-03-概率分布

1. 数据分布与概率分布

1.1. 频数分布与频率分布

1. 频数是各个数据被观测到的次数。
2. 频率是频数除以总次数。

1.2. 累积频数与累积频率

1. 数据排序后(通常是降序)进行频数或者频率的累加。

1.3. 概率分布

1. 我们需要从特定数据到一般规律的抽象，才能奠定数据科学的基础。

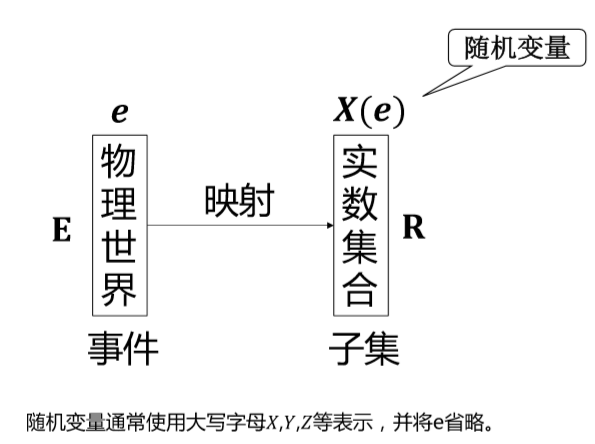
1.3.1. 随机变量

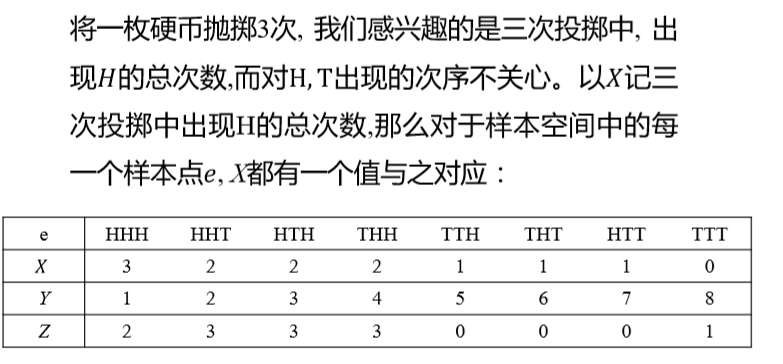
1. 例子:随机变量X，Y，Z
   • X更加符合需求

2. Summary:

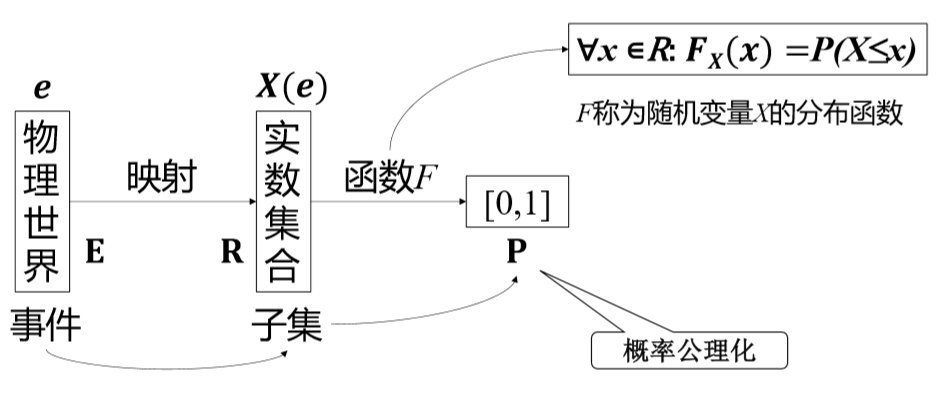
1.3.2. 分布函数

1. 对任意的X进行概率的累加，即从负无穷到X累加构建的一个函数成为随机变量X的分布函数
2. 分布函数一定是左连续的，但是概率密度函数不一定

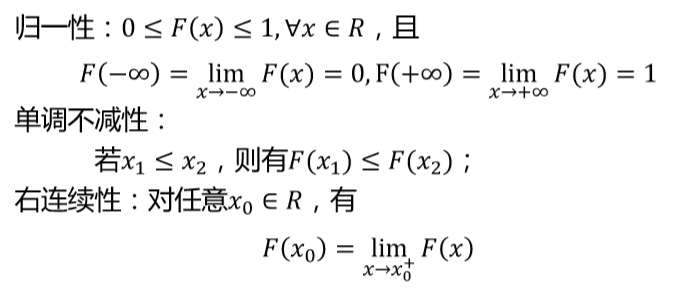
1.4. 随机变量

1. 为了进一步研究概率分布，我们对于随机变量进行深入研究分析。

1.4.1. 离散型随机变量(离散随机变量)

1. 一个随机变量 X 的可能取值为有限个或可列无穷多个, 则称X为离散型随机变量。
2. 概率分布律

3. 之前的抛硬币问题的例子

1.4.2. 连续型随机变量

1. 例子:一个靶子是半径为2米的圆盘,设击中靶上任意同心圆盘上的点的概率与该圆盘的面积成正比,并设射击都能击中靶, 以X表示弹着点于圆心的距离。试求随机变量X的分布函数。

2. 概率密度函数:在断点处未必是连续的
   • 密度函数要求非负可积即可。当然在经典连续概率分布中，密度函数通常也是连续的。一来是比较符合自然世界，二来是容易得出优良的数学性质。

3. 性质:

1.4.3. 强调

1. 随机变量还有其他形式，不是离散的未必是连续的，反之亦然。

2. 矩:数据动力学

2.1. 什么是矩?

1. 矩：是物理学中的一个丰富概念，涉及质量、 形状、空间、运动等各个方面。
2. Eg.力矩

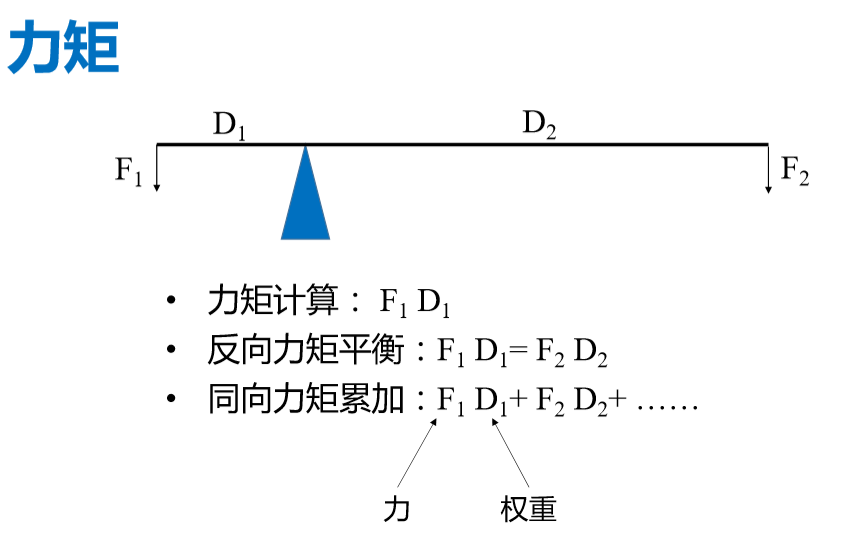
2.2. 数据原点矩

1. 一阶矩是算术平均值，代表数据集的"重心"
2. 二阶矩代表数据集的转动惯量
3. 原点矩代表了数据集跟重量相关的动力度量

2.3. 数据中心距

1. 一阶中心矩B1为零
2. 二阶中心矩B2为方差
3. 三阶中心矩刻画偏度
4. 四阶中心矩刻画峰度
5. 中心矩代表了数据集跟几何相关的动力度量

2.4. 例子

2.5. 数学期望

2.5.1. 离散变量数据期望

2.5.2. 连续随机变量数学期望

2.5.3. 数学期望的性质

1. 对于常数𝐶, 有𝐸(𝐶)=𝐶
2. 对于常数𝐶及随机变量𝑋, 有𝐸(𝐶𝑋)=𝐶𝐸(𝑋)
3. 设𝑋和𝑌为两个随机变量, 则𝐸(𝑋+𝑌)=𝐸(𝑋)+𝐸(𝑌)
4. 设随机变量𝑋和𝑌独立, 则𝐸(𝑋𝑌)=𝐸(𝑋)𝐸(𝑌)

2.6. 方差

2.6.1. 方差的性质

1. 设𝐶是常数，则𝑉𝑎𝑟(𝐶)=0;
2. 设𝑋是随机变量, 𝐶是常数, 则 𝑉𝑎𝑟(𝑋+𝐶)=𝑉𝑎𝑟(𝑋),𝑉𝑎𝑟(𝐶𝑋)=𝐶²𝑉𝑎𝑟(𝑋).
3. 设随机变量𝑋与𝑌相互独立, 则 𝑉𝑎𝑟(𝑋±𝑌)=𝑉𝑎𝑟(𝑋)+𝑉𝑎𝑟(𝑌).

2.7. 概率分布的矩-数字特征

1. 随机变量X的矩定义如下
   • 若𝐸(𝑋^k)存在(𝑘=1,2,⋯), 称𝐸(𝑋^k)为𝑋的𝑘阶原点矩或𝑘阶矩, 记为𝜇_𝑘
   • 若𝐸((𝑋−𝐸𝑋)^k)存在(𝑘=1,2,⋯), 称𝐸((𝑋−𝐸𝑋)^k)为𝑋的𝑘阶中点矩, 记为𝜐_𝑘
2. 中心距的原点矩表示

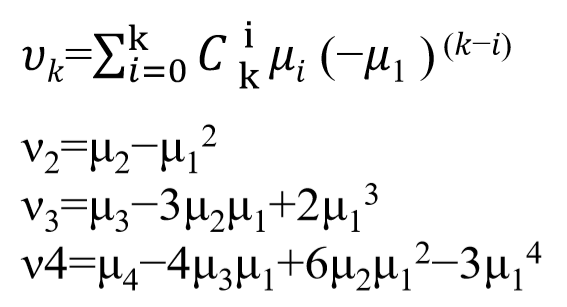
离散概率分布

1. 见离散概率分布