2020-数据科学基础-02-概率基础

02-概率基础

1. 第一节 概率的定义

1.1. 元素与数据之间的映射

1. 样本点:集合元素
2. 样本空间:集合
3. 为何映射集合？
   • 可以应用大量的已有数学模型来进行研究

1.2. 事件的集合表示

1. 样本空间Ω的任意子集 A 称为(随机)事件
2. 观察到样本点e ，若e ∊ A则称这一事件发生

1.2.1. 事件的分类

1. 基本事件：由一个样本点组成的单点集
2. 复合事件：由两个或两个以上样本点组成的集合
3. 必然事件：全集Ω
4. 不可能事件：空集∅
   • 任何实验产生的样本点都不能属于空集
5. 空集和全集都是样本空间的子集，所以都是事件。

1.3. 事件的结合运算

1. 包含：𝐴⊆𝐵，即事件𝐴发生必然导致事件𝐵发生
2. 相等：𝐴=𝐵，即𝐴⊆𝐵且𝐵⊆𝐴
3. 和：𝐴∪𝐵，即𝐴和𝐵至少一个发生
4. 差：𝐴−𝐵，即事件𝐴发生且事件𝐵不发生。
5. 积：𝐴∩𝐵，也记作𝐴𝐵，即事件𝐴和𝐵都发生
6. 互不相容：𝐴𝐵=∅，即𝐴和𝐵不能同时发生
7. 互逆：𝐴∪𝐵=Ω且𝐴𝐵=∅，𝐴和𝐵互逆，通常𝐵记为 𝐴(上划线)

1.3.1. 复杂事件的集合运算表示

1.3.2. 事件发生的频率

1.3.3. 频率的收敛性

1. 这个常数为概率

1.4. 经典概率定义

1.4.1. 古典概率

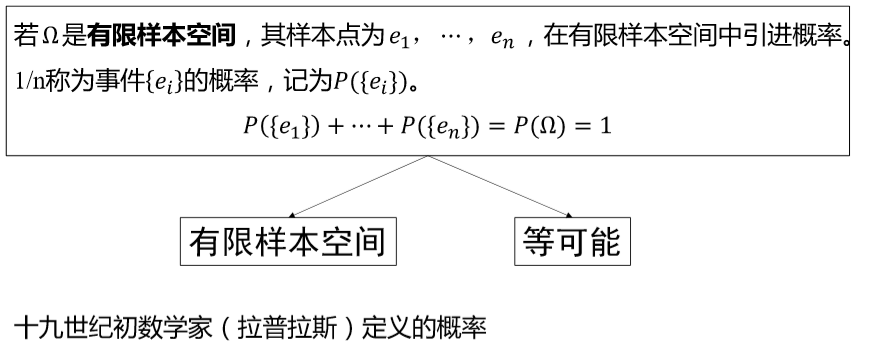
1. 两个重要特性:
   1. 有限样本空间
   2. 等可能

1.4.2. 几何概率

1. 数据表示如何从有限集合到无限集合推广？
2. 例一：某人午觉醒来，发觉表停了，他打开收音机，想听电台报时，求他等待的时间短于10分钟的概率。
3. 例二：在400毫升自来水中有一个大肠杆菌，今从中随机抽出2毫 升水样放到显微镜下观察，求发现大肠杆菌的概率。
4. 一种相当自然的答案是认为例1所求的概率等于<1/6，例2所求的概率等于1/200。在求这些概率时，我们采纳了某种几何特性的等可能假设。
5. 实例:在半径为1的圆内随机地取一条弦，问弦长超过根号3的概率等于多少?
   • 等可能假设不同，结果不同
   • 选择圆心角:1/3，等可能假设:假设在弧上
   • 选择弦心距:1/2，等可能假设:到圆心的距离
   • 选择弦中点:1/4，等可能假设:面积

1.4.3. 小结

1. 在数据映射中，我们需要遵循物理世界到数据集合的某种结构保持。

1.5. 概率的公理化表示

1. 概率的性质

2. 概率的计算

2.1. 条件概率

2.1.1. 引入

1. 已知某一事件已发生，求另一事件发生的概率。
2. 例如考虑有两个孩子的家庭，假定男女出生率一样，则两个孩子(依大小排列)的性别为(男男)，(男女)，(女男)，(女女)的可能性是一样的。
3. 记A为随机选取两娃家庭有一男一女的事件，则𝑃(𝐴)=1/2
4. 如果我们预先知道某个家庭至少有一个女孩(设为事件𝐵)，那么，上述事件A的概率便应是2/3

2.1.2. 条件概率

1. 使用韦恩图来进行说明

2.2. 乘法公式

1. 例子:设某光学仪器厂制造的透镜，第一次落下时打破的概率为1/2，若第一次落下未打破，第二次落下打破的概率为7/10，若前两次落下未打破，第三次落下打破的概率为9/10。试求透镜落下三次后未打破的概率。
   • (1 - 0.5)(1 - 0.7)(1 - 0.9) = 0.015

2.3. 完备事件组

2.4. 全概率公式

1. 练习

1. 2/5 * 1/2 * 3/7 * 1/2 = 3/70

2. 2/3 * 1/2 + 1/3 * 3/4 = 7/12

3. 写法设法参考

2.5. 贝叶斯公式

1. 意义:贝叶斯定理往往与全概率公式同时使用。全概率公式一用于"由因求果"问题，而贝叶斯定理一般用于"执果寻因"问题。
2. 例如，在医疗诊断中，为了诊断到底是哪种疾病，对病人进行观察与检查，确定了某项身体指标(如是体温、验血)，然后采用这类指标来帮助诊断。这时就可以用贝叶斯公式来计算有关概率。
3. 是概率理念的一个巨大进步。

4. 练习:
   • 11/164

2.6. 独立性

1. 和互不相容是完全不一样的，A与B互不相容是指A交B为空
2. 独立在实际中往往是假设。
   • 而不是去求证的目标
3. 独立是一个非常强的假设。

3. 随机测试示例

3.1. 引入

3.2. 问题背景

3.3. 随机测试初步

1. 进一步明确化问题
   • 通过选择部分数字来进行校验

2. 什么时候会出现误判？
   • 求解的时候我们要计算第二种情况下的误判概率
   • 注意单边错误，误判概率:单边错误概率

3. 我们化简到求两个方程的差等于0的根的个数
   • 根据代数基本定理我们可以知道的是我们的根的个数不会大于100个。
   • 概率的模糊估计

3.4. 随机测试改进

1. 我们只需要简单的增加测试用例的数量就可以降低出错的概率

2. 为了进一步降低出错概率，我们多次使用常用的系统分析的手段
   • 使用随机检测

3. 有放回抽样
   • 每次随机取，所以检测错误的概率为1/100
   • 也就是错误概率会成指数型降低

4. 有放回的抽样:
   • 一共有d个根，在第j次的时候，已经提出了j-1个根。
   • 为什么是100d - (j - 1)因为是从100d个数据中选择数字
   • j增大到d的时候，就能将概率降低到0

4. 总结

1. 𝐹(𝑥)无放回抽样的准确率比有放回抽样高。
2. 有放回抽样的算法实现通常比无放回抽样简单。
3. 当𝑑+1次无放回抽样后，能够确保算法的准确性。
4. 但算法复杂度提升到𝑂(𝑑²)。