2020-数据科学基础-01-数据科学

1. 数据科学的角色

1. 数据科学家
2. 数据分析师
3. 数学工程师
4. 问题:不同的术语

1.1. 数据科学的具体角色

1. 收集正确的数据
   • 外部来源的内部数据库
2. 业务分析师了解业务需求
   • 将要求传递给数据分析师
3. 数据分析师 -> 数据科学家(在部分公司中)
   • 理解数据，并确定解决业务问题所需的数据
   • 理解数据和关系并探索数据以确保可以创建模型
   • 如果数据缺失，则返回收集点收集更多的数据
4. 数据工程师
   • 使用数据管道收集数据、清理并转换数据，并尽可能将其聚合到数据库或数据源中去
5. 设计师:
   • 担心数据如何存储，关心字段之间的关系，并且设计存户数据的结构存储
6. 数据库管理员
   • 通过安全访问来正确访问，不是所有人可以访问
   • 备份数据库防止出现数据丢失
7. 数据架构师
   • 设计所有工作原理的架构(多长时间更新一次)
8. 数据科学家
   • 分析输入，建立模型，进行预测
   • 从很多的模型中选择合适的模型
   • 更多的工作是基于数据理解的参数微调 -> 超参数
9. 机器学习研究人员:
   • 更关注研究机器学习模型
10. 机器学习工程师
    • 部署模型，获得正确输入和输出以及风险
    • 保护部署的机器的模型，监视机器
11. 全局业务或流程设计师 或 业务架构师 或 企业架构师
    • 完成端到端的部署

2. 数据信息知识

1. 主要将DIKW模型

2.1. DIKW金字塔

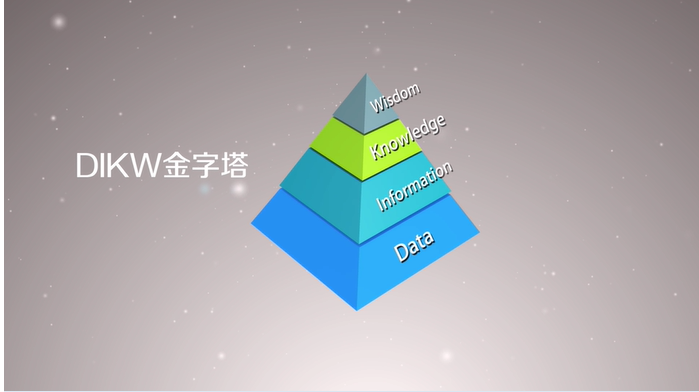
2.2. 数据

1. 数据来自符号和标识，往往是可以表示抽象事实的物体。
   • 数据可以通过矩阵描述
   • 可以是字符串
2. 数据可以运算和处理
3. 数据最相关的集合论
4. 编码:从一种形式或格式转化为另一种形式

2.3. 数学结构

1. 在数学中，一个集合上的结构是由附加在该集合上的某种操作和含义

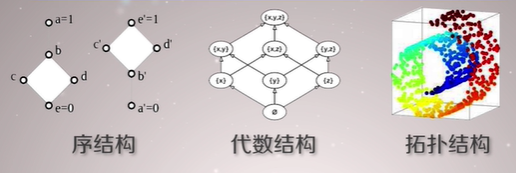
2.3.1. 序结构

1. 全序关系:任意两个关系可比
2. 任意良序关系一定是全序关系
3. 身份证的序结构

2.3.2. 代数结构

2.3.3. 逻辑规则

2.4. 信息

1. 信息来自于给定环境的数据
2. 信息不等同于数据

2.5. 知识

1. 知识一旦符号化或者客观化就削减成为信息

2.6. 智慧

1. 智慧是知道什么是正确应该做的东西，需要是非感

3. 数据类型

1. 我们关注的数学数据类型

3.1. 根据数据类型选择统计做表方式

1. 分类型数据:
   • 饼图
   • 柱状图
   • 横向柱状图
2. 定序数据
   • 柱状图，按照次序
3. 数值型数据
   • 折线图
   • 直方图
   • 盒形图

3.2. 常见数据类型

1. 定类数据
2. 定序数据
3. 定距数据
4. 定比数据
5. 从上到下:从低级别到高级别
6. 高级数据可以通过数据处理降为低级别数据
   • 低级别数据可以实用的方法，高级别数据也是适用的

3.2.1. 定类数据

3.2.2. 定序数据

3.2.3. 定距数据

1. 零点是强制规定的，并不代表完全没有

3.2.4. 定比数据

1. 零点是有完全没有的含义的

3.2.5. 其他数据类型

4. 数据汇总

4.1. 度量方式

1. 集中趋势度量
2. 离散趋势度量
3. 形态趋势度量

4.2. 集中趋势度量

4.2.1. 众数

1. 一批数据中出现次数最多的那个数值，通常记为M
2. 众数不受极值的影响。众数通常用来描述离散型变量，尤其是分类型变量。

4.2.2. 中位数

4.2.3. 四分位数

1. 四分位数的计算

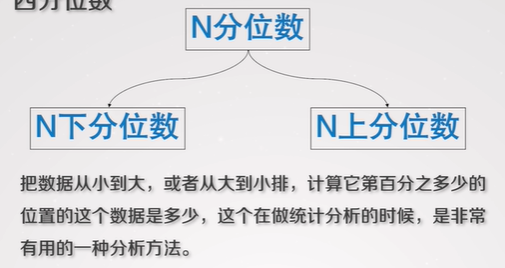
4.2.4. N分位数

1. N下分位数
2. N上分位数

4.2.5. (算术)平均数

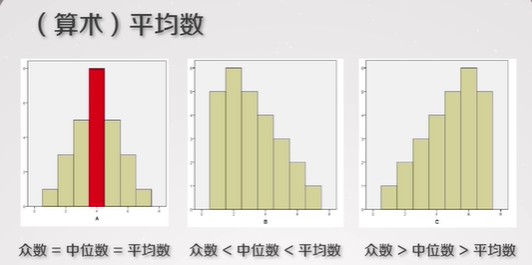
1. 上图:正常、右倾、左倾

   • 数据偏移是根据重心(均值)确定的

2. 具有求和稳定性

4.2.6. 加权平均数

1. 有对应的权
   • 权重的设置通常要求代表某种性质如重要性、频繁度等。

4.2.7. 几何平均数

1. 例子:累积增长

2. 取对数->算术平均数

4.2.8. 调和平均数

4.2.9. 平方平均数

1. 量纲一致

4.2.10. 平均数不等式

4.3. 离散趋势度量

1. 研究数据的波动

4.3.1. 全距

4.3.2. 内距

4.3.3. 偏差平方和

1. 为什么用算术平均值做偏差
   • 算术平均值有偏差极小型

4.3.4. 方差和标准差

1. 定义式和计算式

2. 平方的和减去和的平方作为偏差平方和

4.4. 思考

1. 对数在数据预处理中的作用?
2. 如何建立集中趋势度量和离散趋势度量之间的关系。

5. 作业

1. ABCD
2. 在第一章的课程中，老师为我们介绍了逻辑推理规则，即逻辑三段论推理规则，我们赋一个规则，它的前提条件满足，则可以得到结论，((p->q)^p)->q。此外，我在课外了解到，知识的推理分析，还包含直接推理、间接推理等多种推理形式。
3. ABCD ?
4. B
5. 答案
   • 全距，又称极差，是样本观察值的最大值和最小值的差。全距是最简单的一种离散趋势度量，通常用来反映一批数据总的离散趋势，但全距不考虑数据的分布情况。当数据中存在极值并不太关注数据分布时，全距是一种合适的离散趋势度量
   • 内距，又称内四分位距，内四分位距用来描述50%的样本观察值的离散趋势度量。它是样本观察值的第三四分位数与第一四分位树的差。内距比全距更有意义，但是仍然有两个缺点:一是不能提供精确的数据分布信息，二是不能用来进行精确的统计推断。