2020-数据管理基础-ch06-数据库设计
ch06-数据库管理
1. 数据库设计
- 数据库设计是研究数据项的基本属性与他们之间的相互关系。
- 该逻辑数据模型包含以数据定义语言生成设计所需的所有必需的逻辑和物理设计选择以及物理存储参数,然后可以使用这些定义来创建数据库。
- 完全属性化的数据模型包含每个实体的详细属性。
1.1. 如何进行数据库设计
- 分析数据库实体
- 列举数据库的数据项
- 决定数据库的每一行的数据项的数据类型
1.2. 数据库设计的问题
1.2.1. 数据冗余:大量重复数据
- 浪费磁盘空间
- 不分表,则会导致大量的数据冗余

1.2.2. 修改异常
- 修改异常浪费时间,并且用户容易造成错误。
- 在修改一个数据的时候,会导致大量数据列的修改。
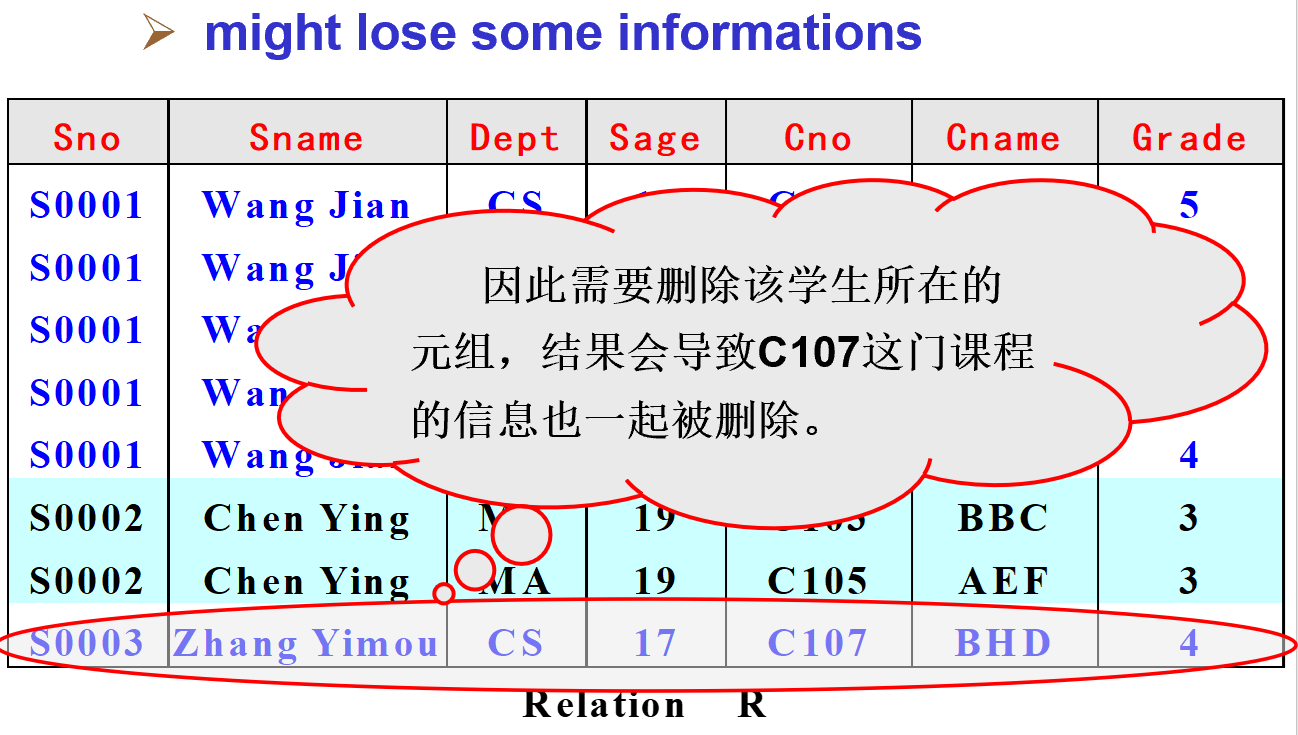
1.2.3. 删除异常
- 删除一个信息实体的同时,可能会导致其他实体信息被同时删除。
1.2.4. 插入异常
- 实体不完全是无法进行插入的
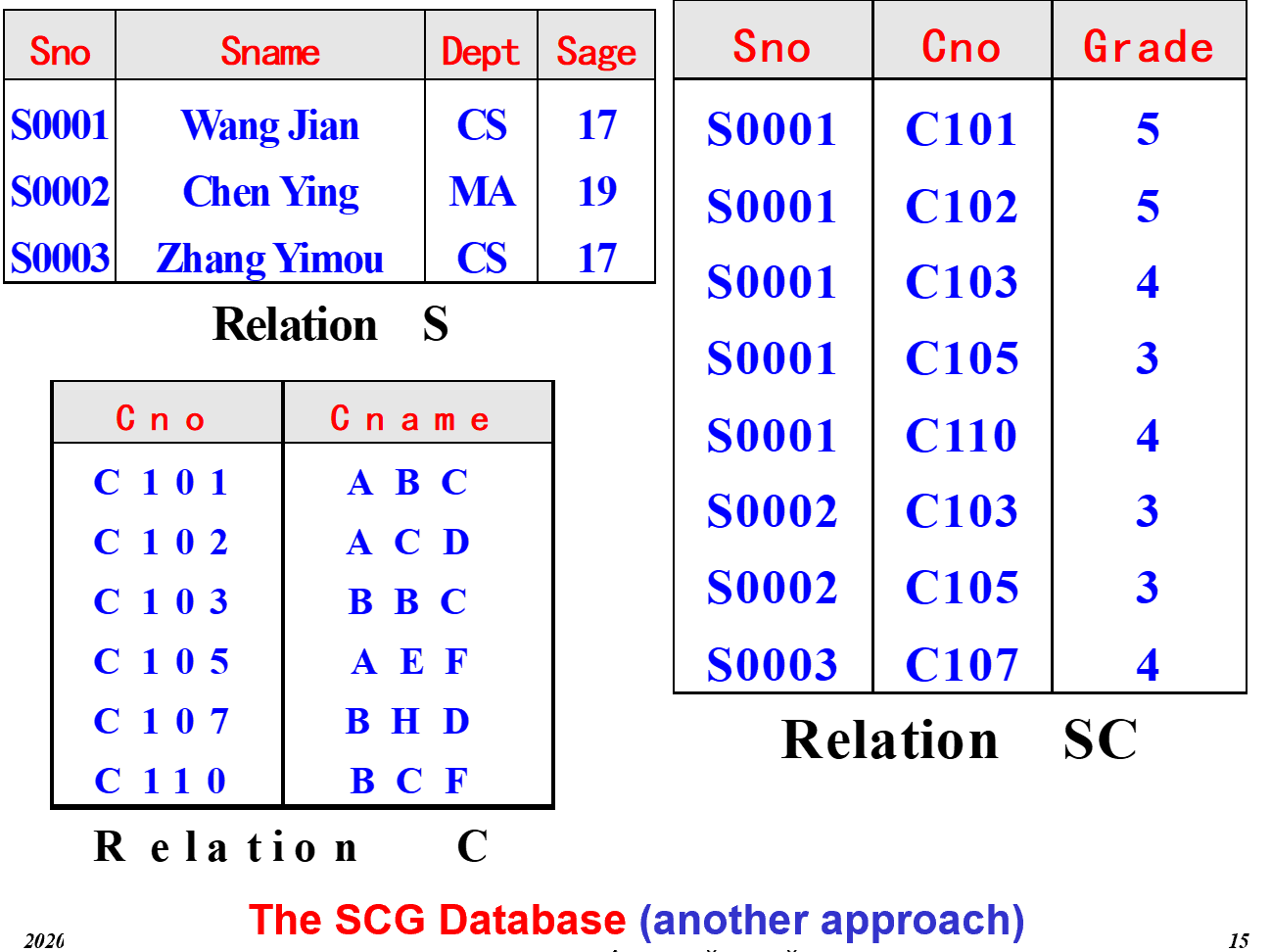
2. ER模型
2.1. 模型的概念
- ER模型是一种用来描述数据库的抽象方式
- 实体关系模型是一种设计方法,更直观,机械更少,但基本上导致了相同的最终设计。
2.2. 模型的组成部分
2.2.1. 实体
- 实体是具有公共属性的可区分的现实世界对象的集合。
- 一个实体对应一个关系表,是一组物体。
- 每一行都是一个实体,或者一个实体的实例,代表一个物体。
- 实体是用长方形表示的
2.2.2. 属性
- 属性是描述实体或关系(定义如下)的属性的数据项。
- 属性是椭圆形表示,单值属性用单实线连接,多值属性用双实线连接
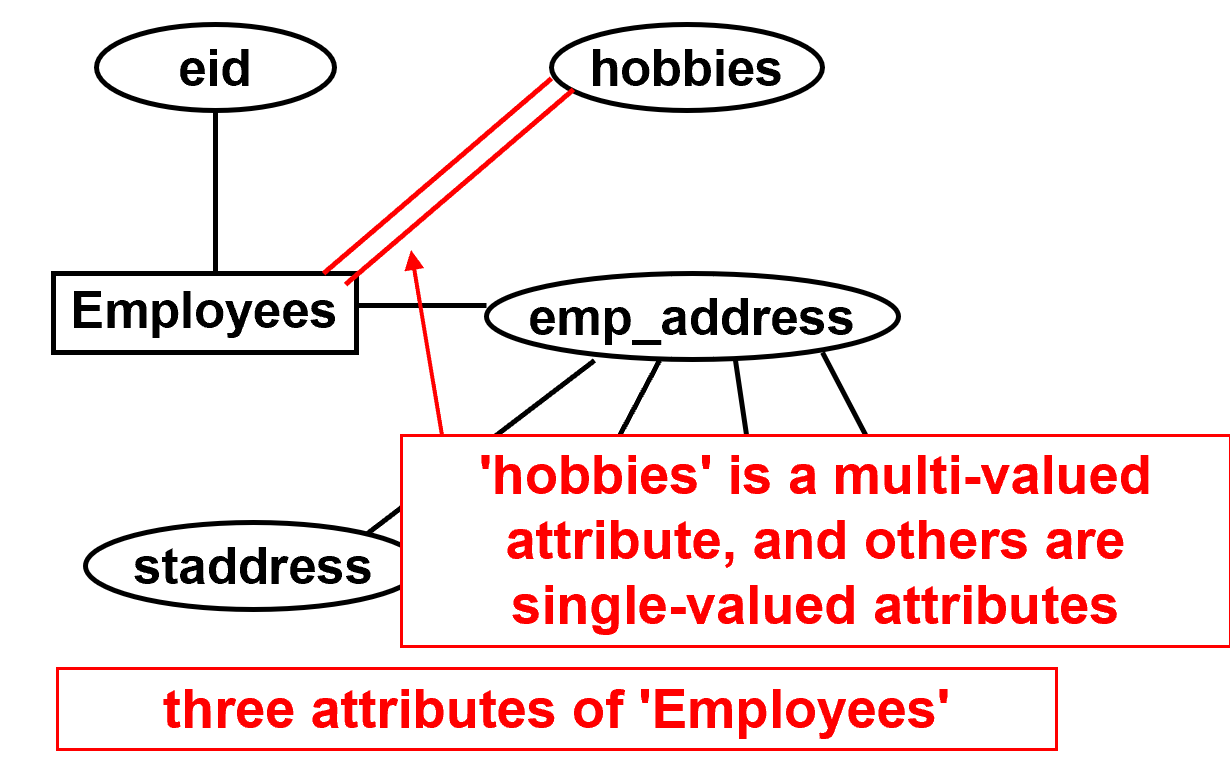
- 特殊的属性
- 候选键:标识符是唯一标识实体实例的属性或属性集。
- 主键
- 候选键和主键在名字下面用下划线表示。
- 描述符:描述符是一个非键属性
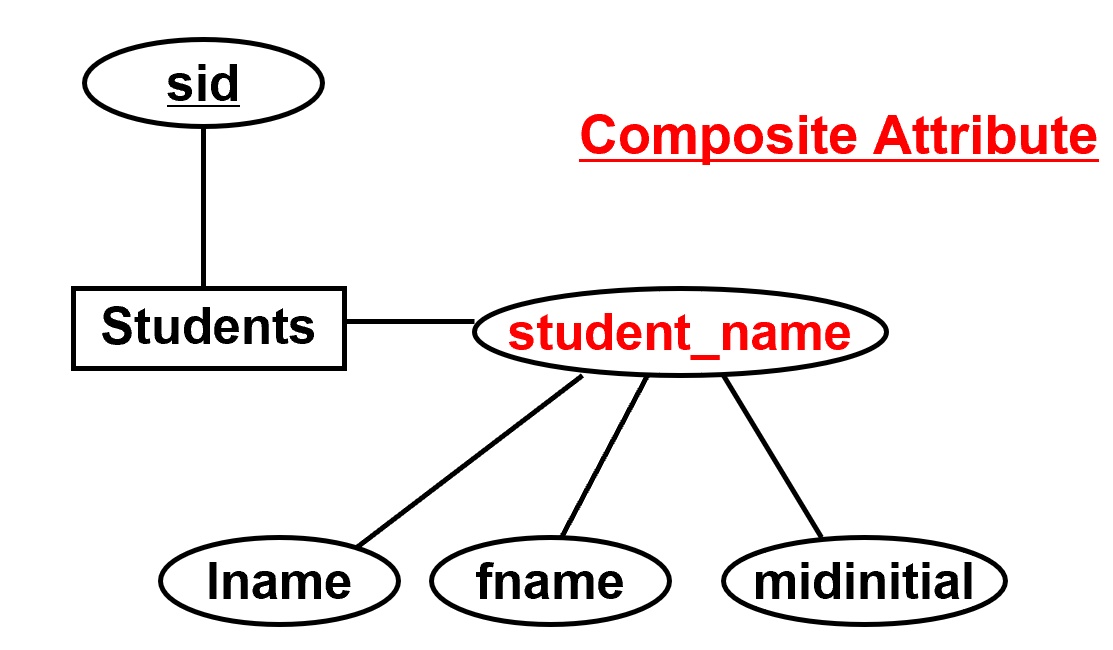
- 复合属性:一组共同描述属性的简单属性,student_name是复合属性,符合属性使用单值和多值属性复合而成
2.2.3. 关系
- 给定m个实体的有序列表,分别为E1,E2,…Em,(同一实体在列表中可能出现多次)
- 关系R定义了这些实体的实例之间的对应规则。
- 具体来说,R代表一组m元组,这是实体实例的笛卡尔积的子集。
- 关系是用菱形表示的
- 关系可以有额外的属性
- 关系可以有环出现
2.3. 实体参与关系的基数
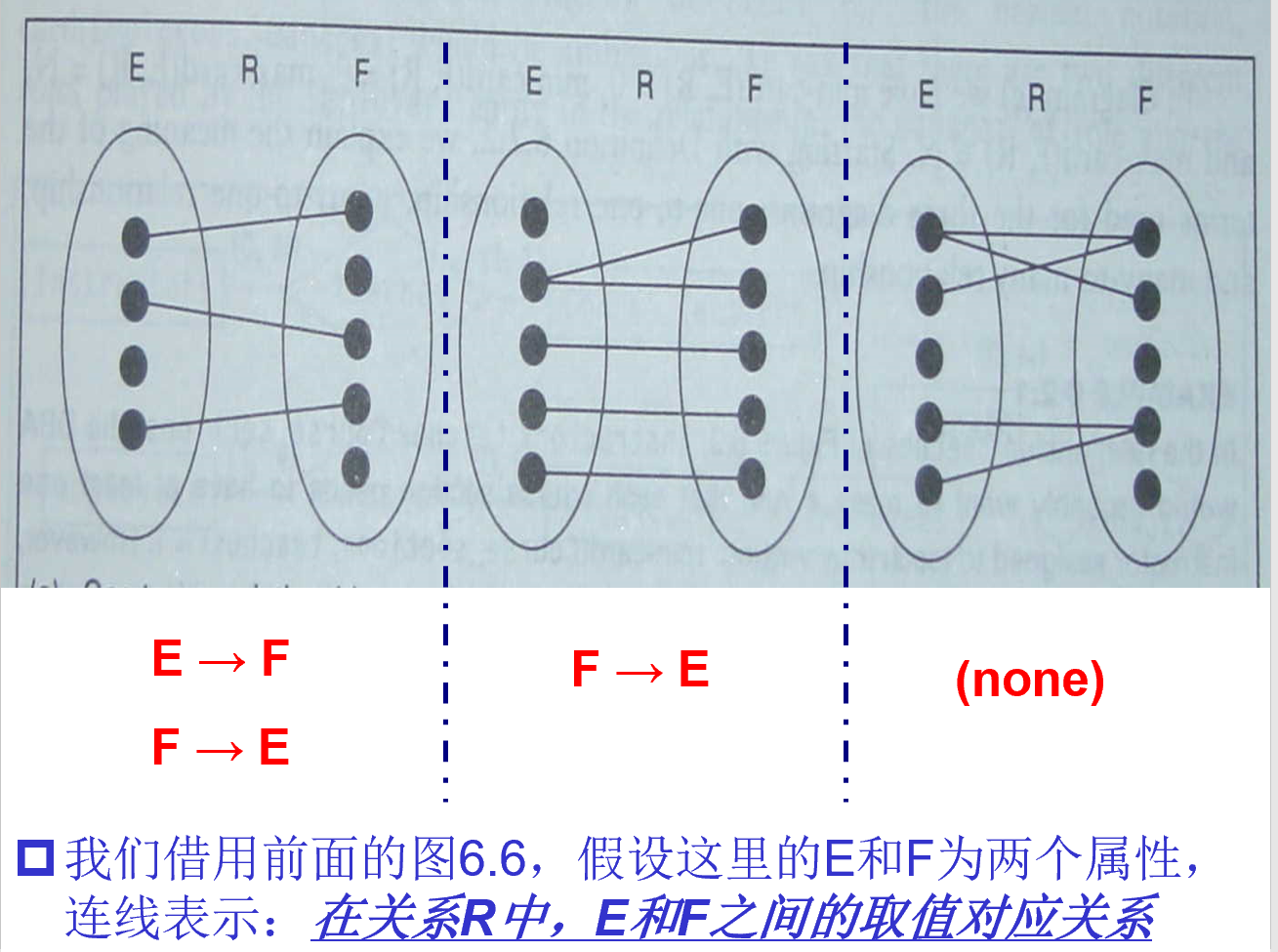
- 实体E和F,关系R,下图中点是实体的实例,线是关系实例
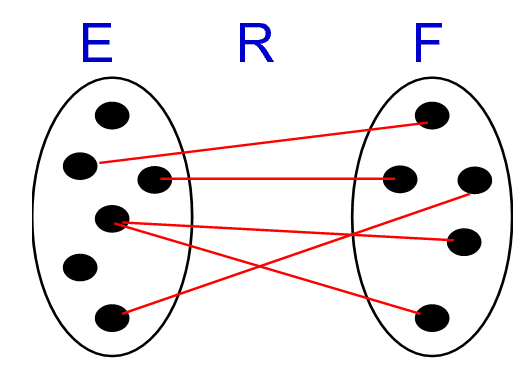
- 如果实体E中的所有实例最多只有一个关系相关,则max-card(E, R) = 1
- 如果实体E中的所有实例有超过一个关系相关,则max-card(E, R) = N
- 如果实体E中所有实例最少只有一个关系相关,则min-card(E, R) = 1
- 如果实体E中所有实例中有没有关系相关的,则min-card(E, R)= 0
- 只有如上这四种情况
2.3.1. card(E, R)
- card(E, R) = (0, N), (min-card(E, R), max-card(E, R))
- 每一个关系都有这样的一组
2.3.2. max-card()
- max-card(X, R) = 1:单值参与
- max-card(X, R) = N:多值参与
2.3.3. min-card()
- min-card(X, R) = 1:强制参与
- min-card(X, R) = 0:可选参与
2.3.4. 多种关系
- 一对一关系
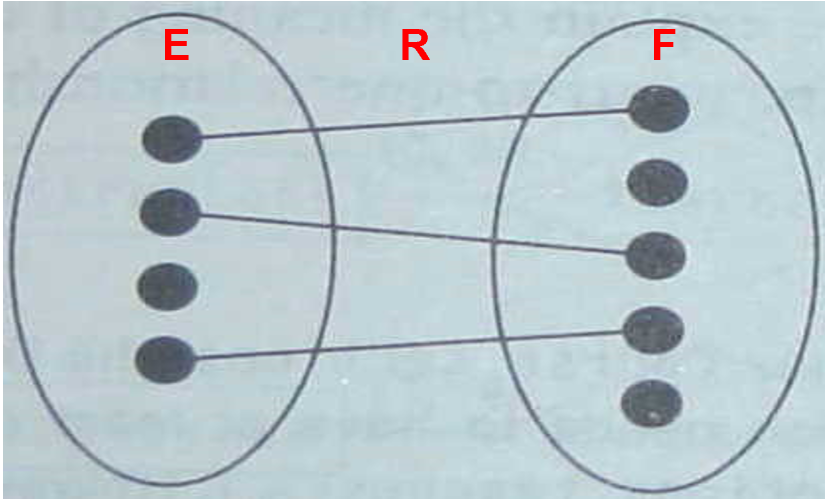
- 多对多关系
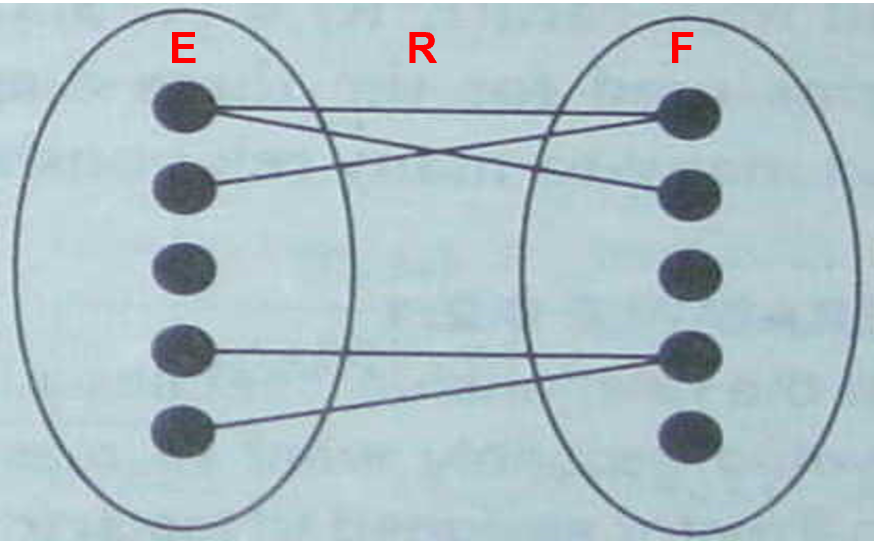
- 一对多关系
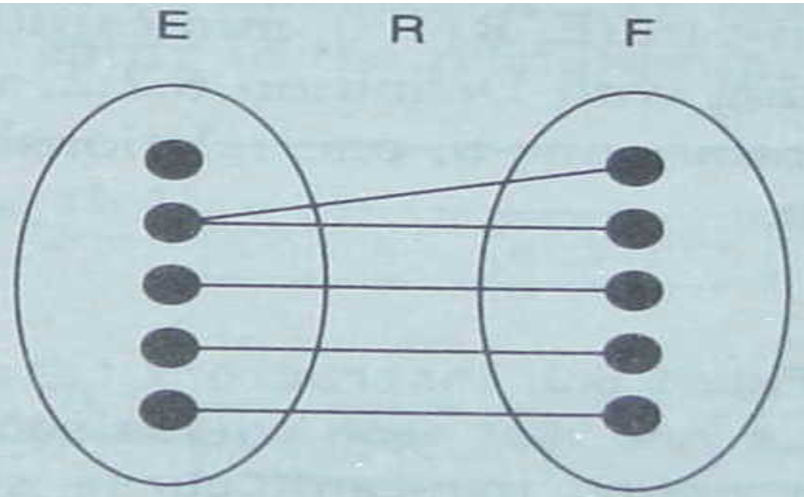
2.4. ER模型的转换规则
2.4.1. 转换规则一
- 实体映射到单个表。实体的单值属性映射到列(复合属性映射到多个简单列)。
- 实体出现成为表的行。
2.4.2. 转换规则二
- 多值属性必须映射到其自己的表。
- 对于ORDBMS并不适用
2.4.3. 转换规则三(多对多关系规则)
- 将二元联系转换为关系(N-N关系):当两个实体E和F参与多对多二进制关系R时,该关系将映射到相关关系数据库设计中的代表表T。
- T还包含附加到关系的所有属性的列。
2.4.4. 转换规则四(多对一关系规则)
- 在具有单值参与的实体(“多面”)中用外键表示。
- 如果max-card(F, R) = 1,每一个对应关系可以用外键来关联。
2.4.5. 转换规则五(一对一关系规则,一侧可选)
- 表示为两个表的外键列在一个具有强制参与的表中:定义为NOT NULL的列。
2.4.6. 转换规则六(一对一关系规则,双侧必选)
- 永远不会分裂。 将其视为单个表中的两个实体是适当的。
2.4.7. ER图绘制和关系模式的模式
- PPT ch06_exp_of_641.pptx
- PPT ch06_exp_of_642.pptx
- PPT ch06_exp_of_643.pptx 注意备注,和帖子
- PPT ch06_exp_of_644.pptx 比较复杂并且综合的一个例子
- 课本253页-255页例子
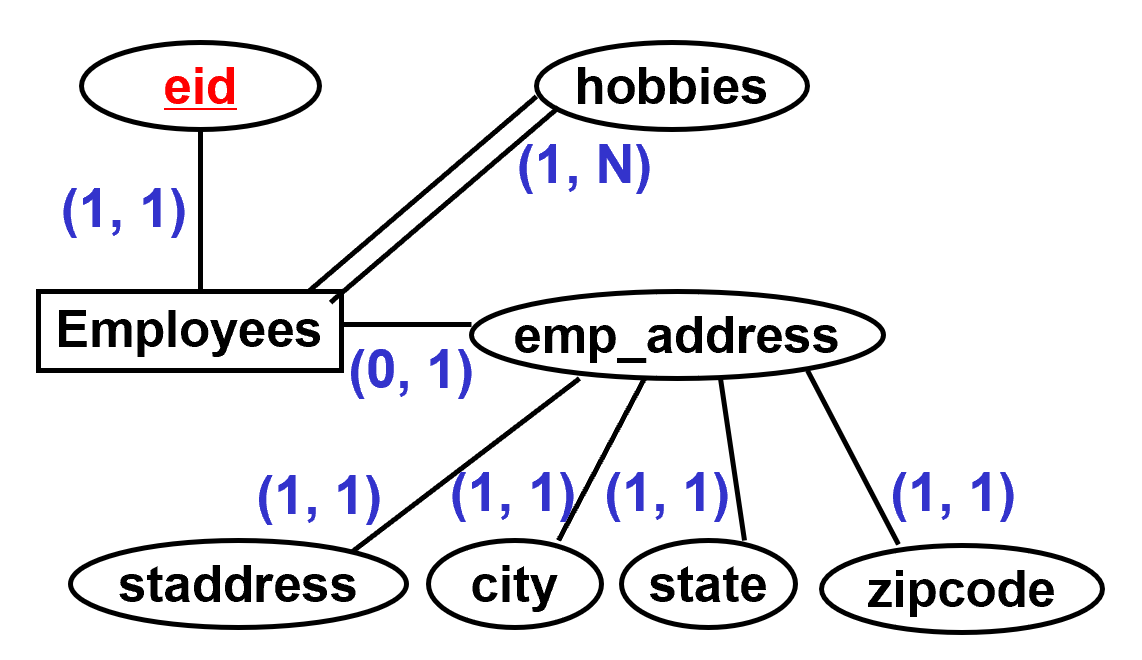
2.5. 一些关系的例子
- (0, ?) means don’t have to say not null (optional)
- midinitial, emp_address
- (1, ?) means do (mandatory)
- sid, student_name, lname, fname, city, …
- (?, 1) single valued attribute
- sid, eid
- (?, N) multi-valued
- hobbies
2.6. 弱实体
- 弱实体是这样一种实体,其出现通过关系R依赖于另一个(强)实体的出现而存在。
2.7. 继承层次
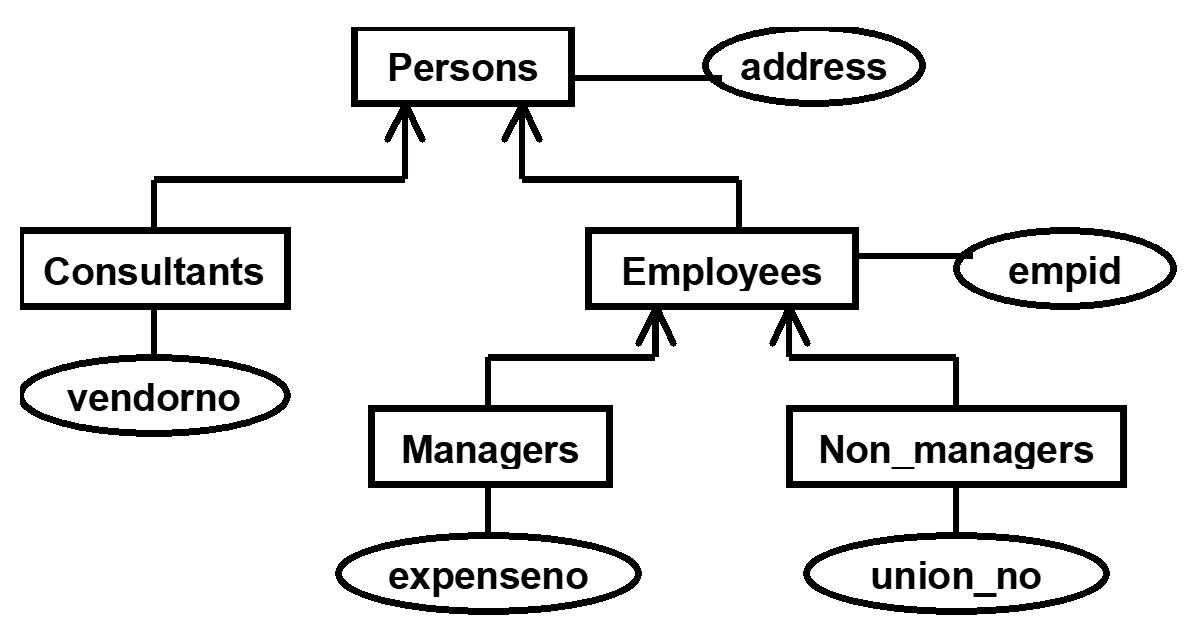
3. 规范化
3.1. NF:Normal Form,范式
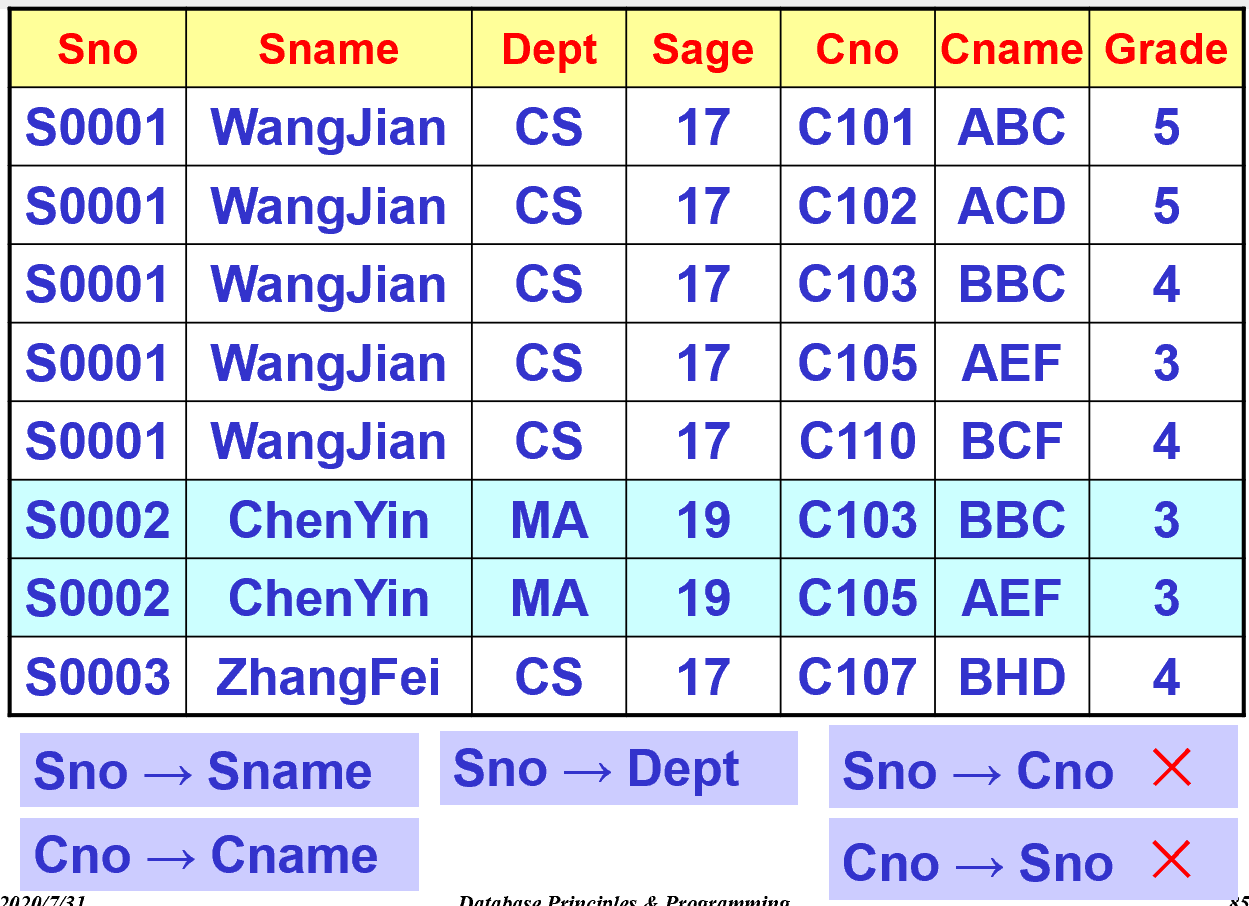
3.2. Functional Dependency (FD, 函数依赖)
- A→B:A在函数上决定B,或者B在功能上取决于A
- 逻辑上的含义
1 | |
- 也就是A的任何一个值都在B中有一个值对应(函数图像关系)
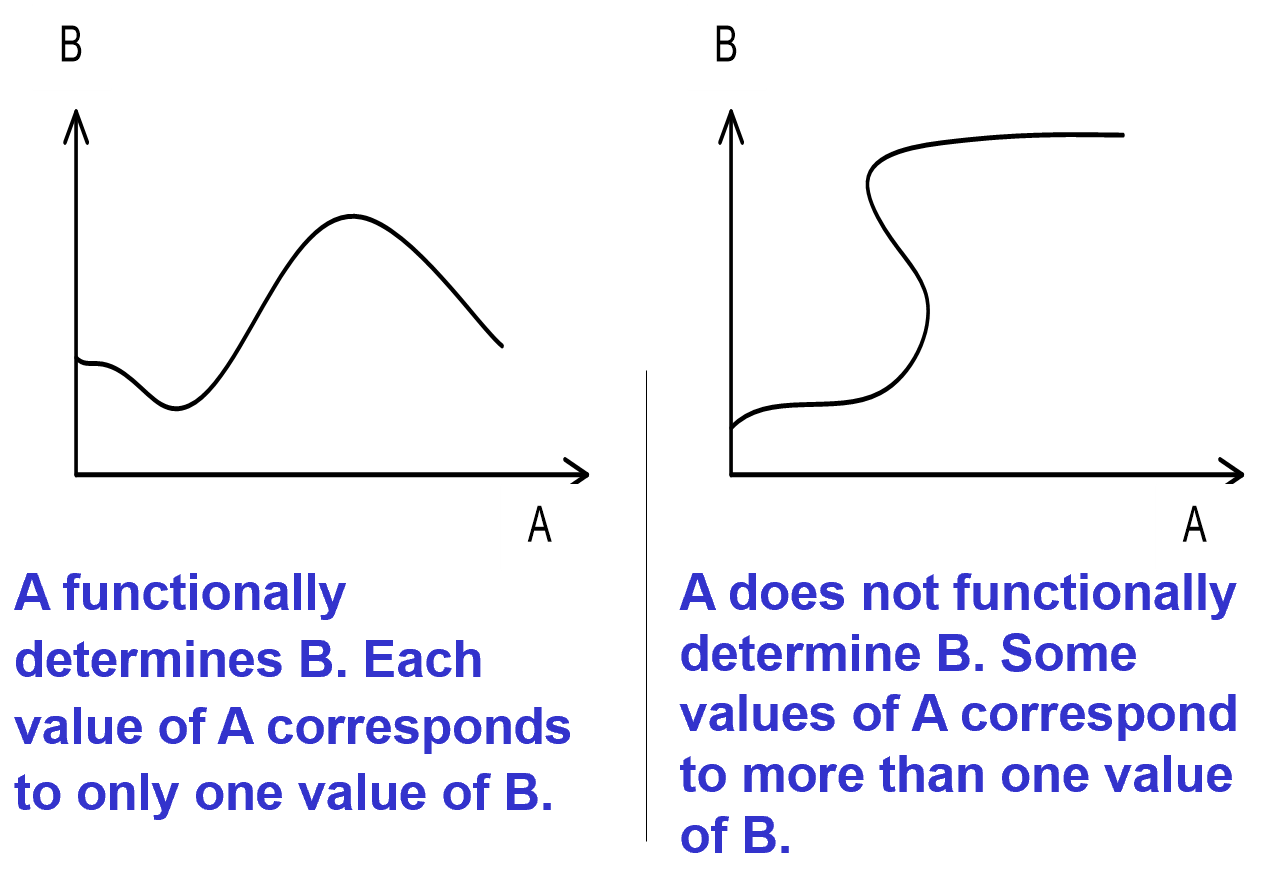
- ER图的关系:可以通过将表转换成ER图,然后快速地了解到函数依赖关系
3.3. Armstrong’s Axioms (Armstrong公理)
- 从已知的一些函数依赖,可以推导出另外一些函数依赖,这就需要一系列推理规则。
- 函数依赖的推理规则最早出现在1974年W.W.Armstrong 的论文里,这些规则常被称作"Armstrong 公理"
- 最基本的推理规则只有3条,由这3条基本规则可以定义出若干条‘扩充规则’
3.3.1. 基本规则
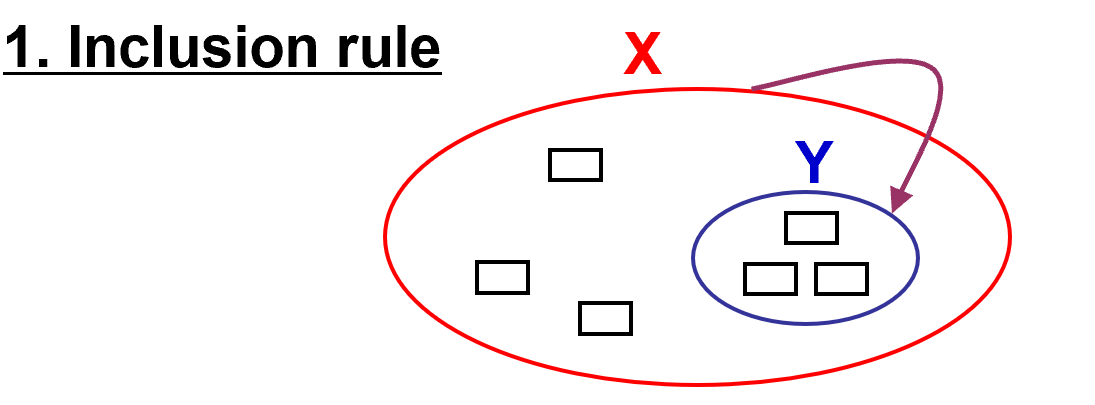
- 规则一:自反规则:If Y 包含于 X,then X -> Y
1 | |
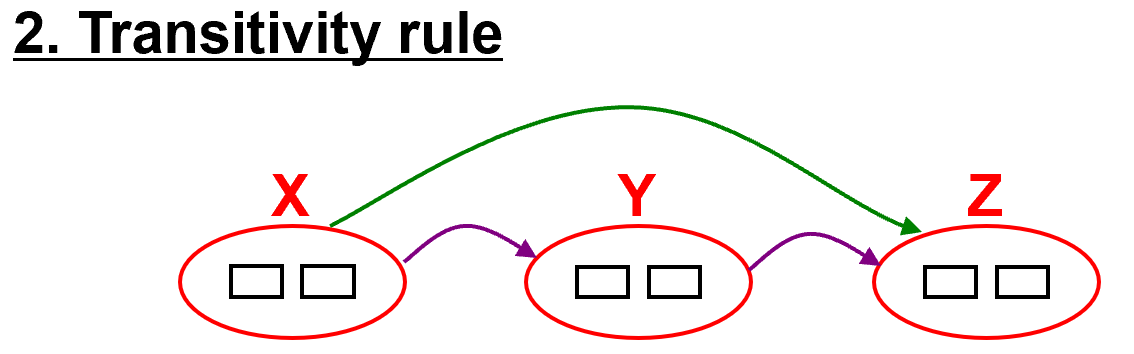
- 规则二:传递规则:If X -> Y, Y -> Z, then X -> Z
1 | |
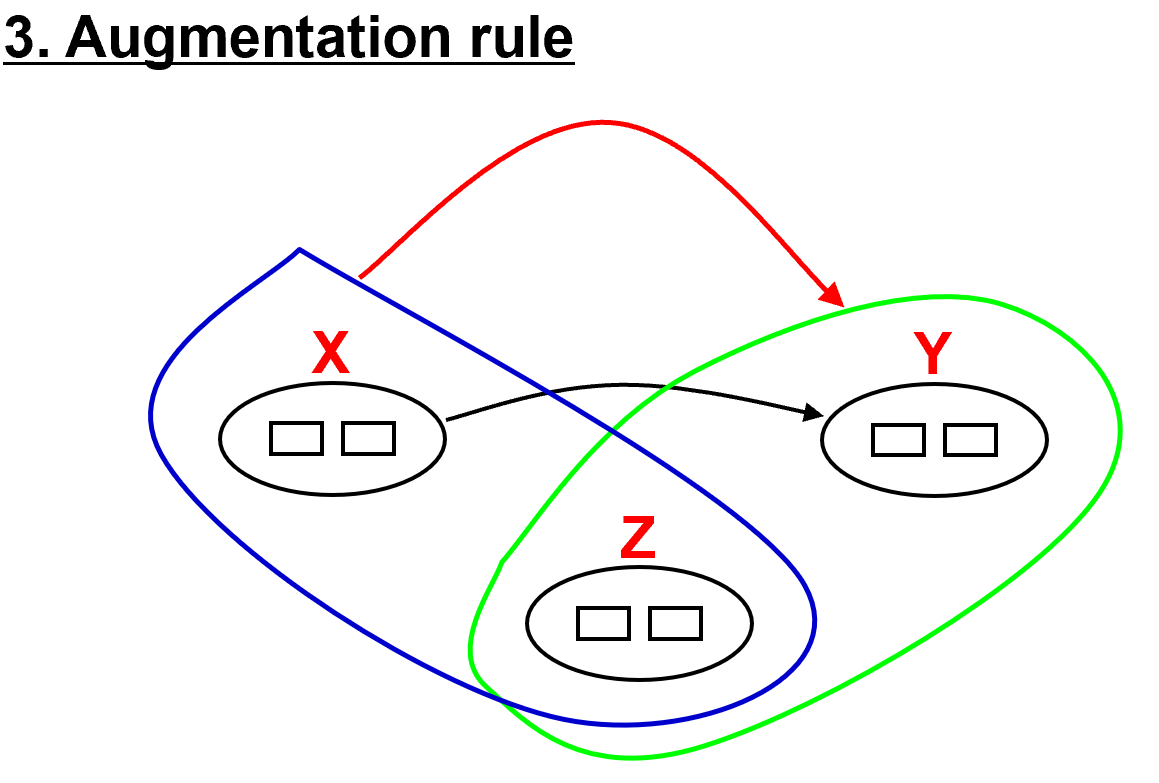
- 规则三:增广规则:If X -> Y, XZ -> YZ
1 | |
3.3.2. 扩展规则
- 合并规则:If X -> Y and X -> Z ,then X -> YZ
1 | |
- 分解规则:If X -> YZ,then X -> Y,and X -> Z
1 | |
- 伪传递规则:If X -> Y,and WY -> Z,then XW -> Z
1 | |
- 聚集规则:If X -> Y,and WY -> Z,then XW -> Z
1 | |
3.3.3. 在表格上寻找最小依赖
- 寻找单个的最小依赖
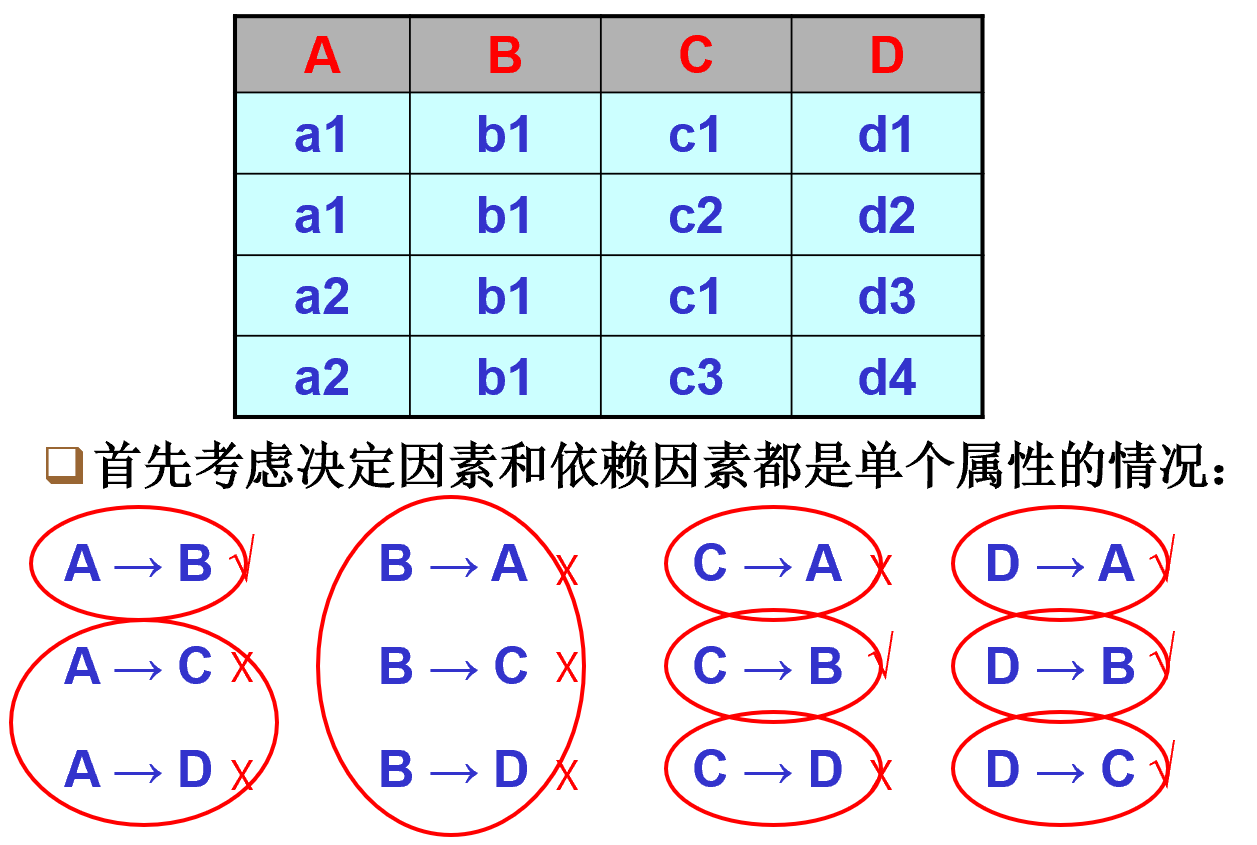
- 将可以合并的依赖进行合并
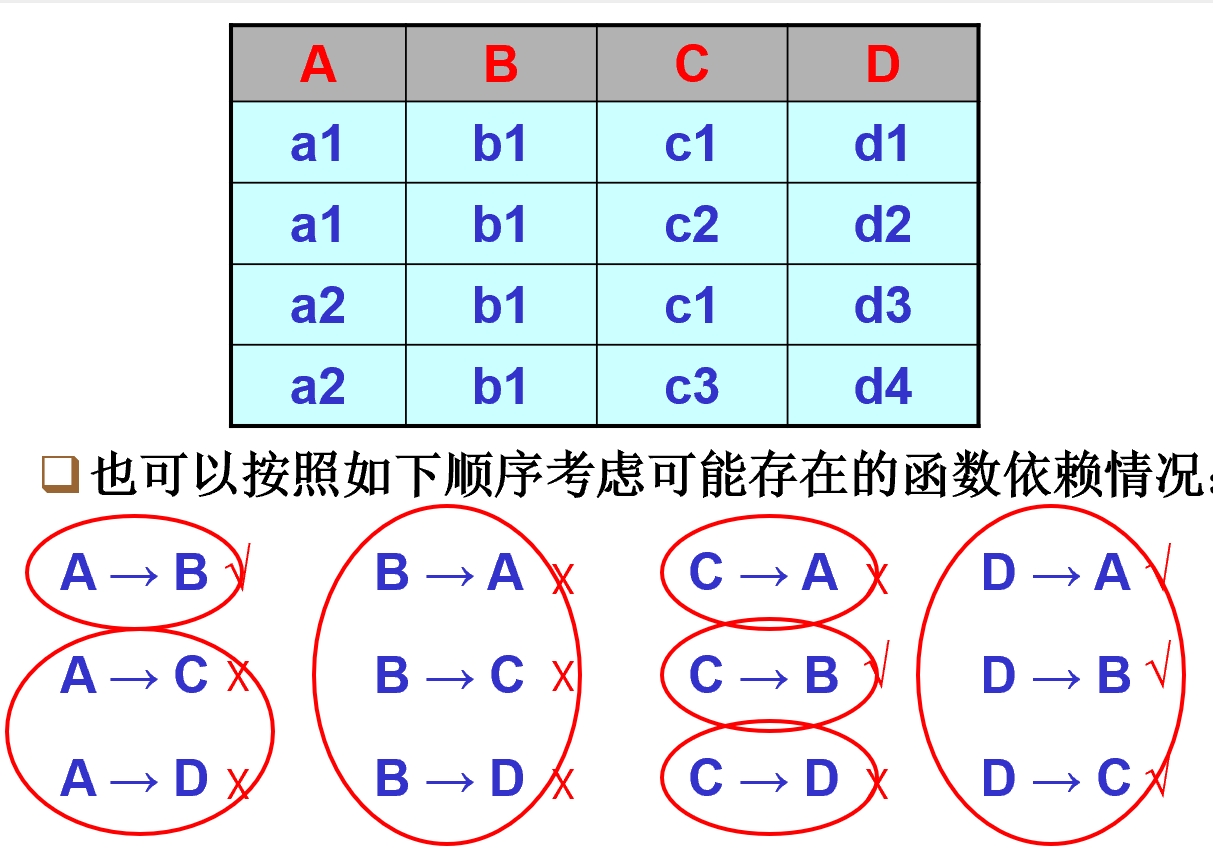
- 考虑需要考虑的多种依赖:D能分别决定其他任何一个,B被其他任何一个决定,B是完全一样的

- 考虑最后一个依赖
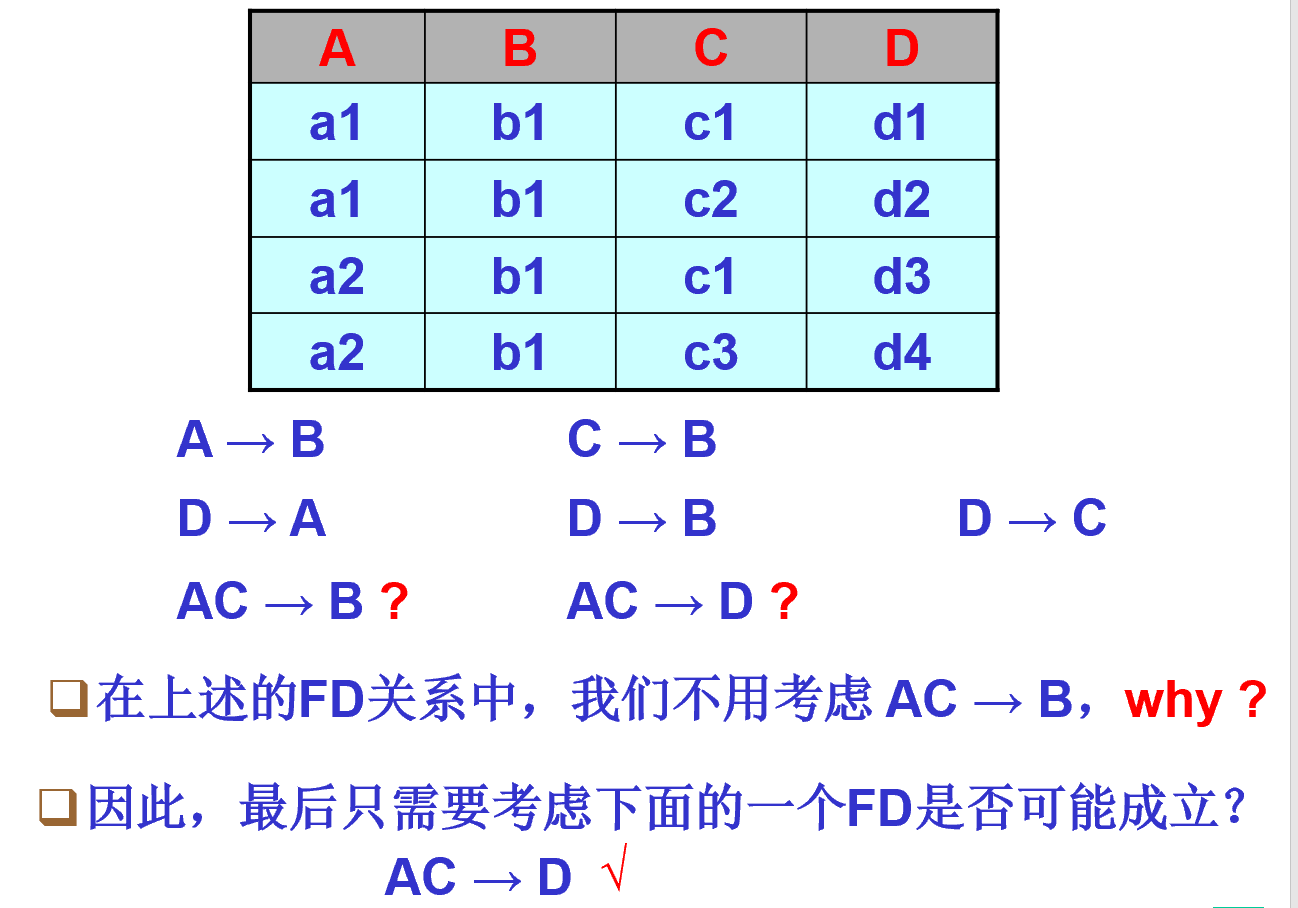
- 最终的结果
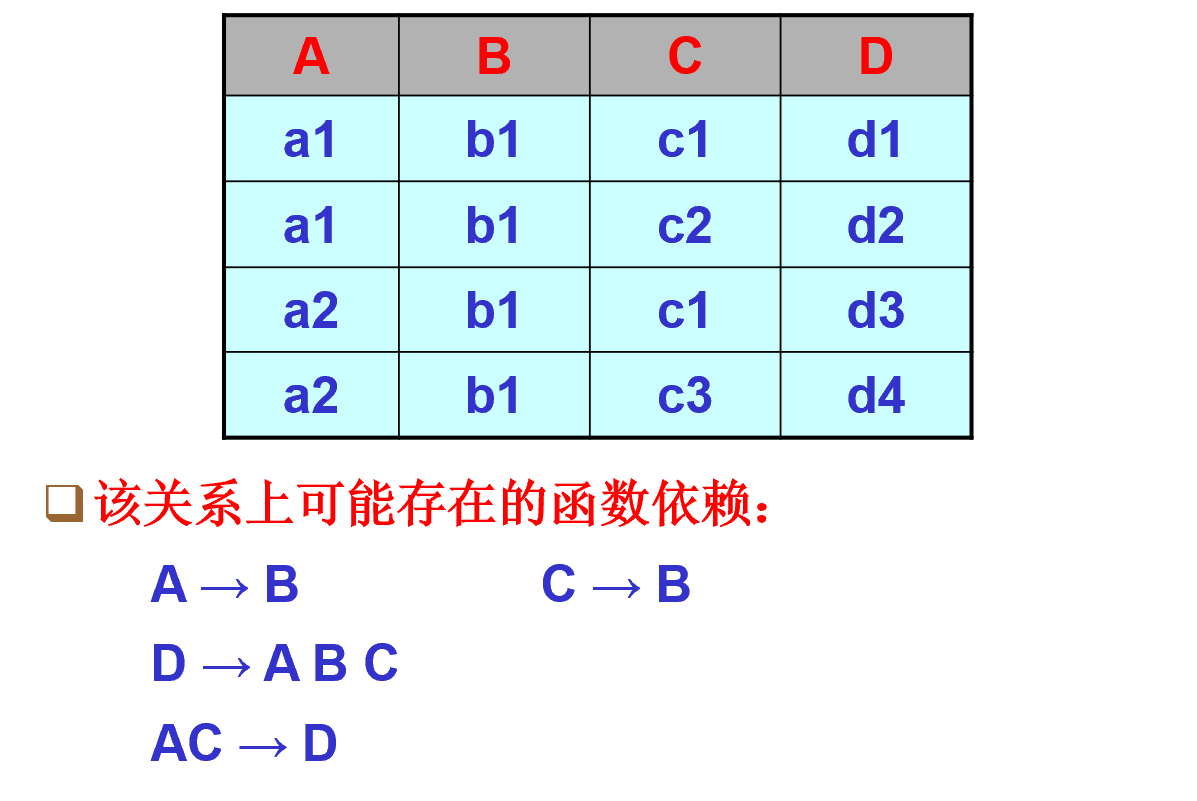
- 一些问题和思考

- 参考课本264-265页
3.4. Closure of a Set of FDs (函数依赖集F的闭包)
- 闭包,记为
- 给定关于表T的属性的FD集合F,我们将F的CLOSURE(用 表示)定义为F隐含的所有FD的集合。
- F中有两个FD(a)和(b)。根据阿姆斯特朗的公理以及(a)和(b),我们可以得到一个新的FD©,然后©是F所隐含的FD。
- 如果FD(d)是琐碎的依存关系(A→A,B→B等),则(d)是F隐含的FD。
- 就是当前集合能扩展出来的所有的函数依赖集

- 例子:PPT ch06_exp_of_FDclo.ppt
3.5. FD Set Cover (函数依赖集的覆盖)
- 表T上的函数依赖集F覆盖了表T上的函数依赖集G当且仅当G可以通过推导关系推导出F,也就是 G 包含于
- 函数依赖集的等价:F 覆盖 G 并且 G 覆盖 F
- PPT 119-124页:详细过程

3.6. Closure of a Set of Attributes (属性集的闭包)
- 我们给定表T上的一个属性集合X,表T上的一个属性集合F,我们定义X在F下的闭包(我们记为 或者是 )是在函数依赖集F的闭包上的X->Y的属性Y的最大集合
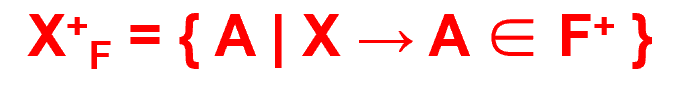

- 例子


- 课本267页的紧凑表示法
3.7. Minimal Cover (最小覆盖)
- 最小覆盖是函数集合M覆盖了函数集合F
- 没有冗余的函数依赖
- 每一个函数依赖的左边都没有多余的属性
3.7.1. 最小覆盖的步骤
- 从函数集合F中,我们创建一个等效的函数集合H,仅在右侧具有单个属性。(直接分解)
- 从函数集合H中,连续删除H中无意义的单个函数集合,无意义是指通过其他的部分我们可以推理出来
- 从函数集合H中,用结果左侧不变的函数连续替换单个函数,只要结果不变H+。(前一个能推导出后一个)
- 开始最小化左侧的集合,从多余一个的左侧集合每次移除一个
- 这里发生变化,需要退回到第2步循环操作
- 从其余的FD集中,收集所有具有相同左手边的FD,并使用并集规则创建一个等效的FD集M,其中所有左手边都是唯一的。简单来说就是把左侧合并
3.7.2. 最小覆盖的例子
- PPT ch06_exp_of_668.ppt
- ABD->A/B/D没有意义
- PPT ch06_exp_of_min_cover.ppt
- 课本268-269页
4. 表格分解
4.1. 规约化的过程
- 分解表:将一个表分解成两个或者更多的小表。
- 但是在分解表的时候并不能经常保证蕴含了原来表的全部信息:有损分解,如下
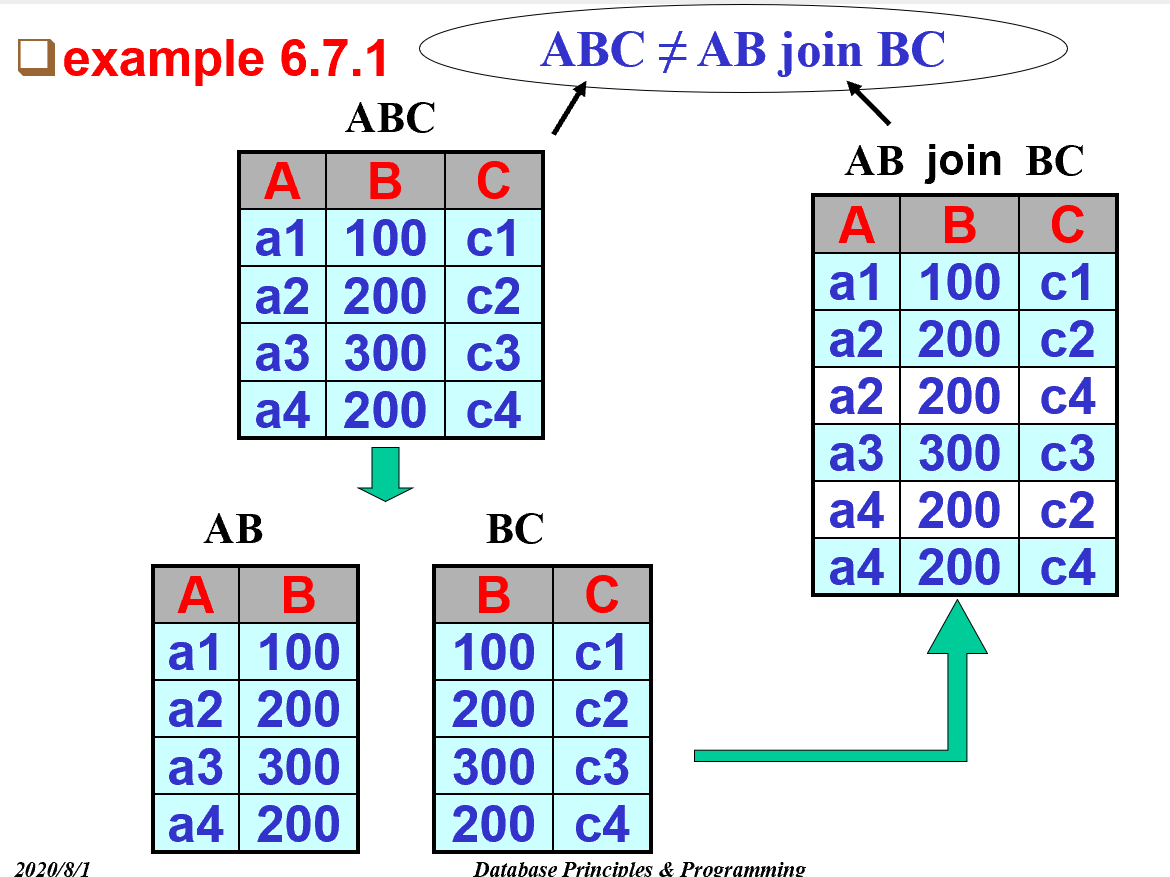
4.2. 无损分解
- 对于具有相关功能依赖集F的任何表T,将T分解为k个表就是具有两个属性的一组表{T1,T2,…,Tk}:
- 在集合中的每一个表Ti,Head(Ti)都是Head(T)的一个子集
- 给定T的任何特定含量,由于分解,T的行将投影到每个Ti的列上。
- 如果对于T的任何将来可能的内容,F中的函数依赖集保证满足以下关系,则将表T与函数依赖集的关联集F的分解称为无损分解:T = T1 join T2 join … join Tk
- 给定一个具有在F上有效的FD集合F的表T,则如果F暗示以下功能依赖性之一,则将T分解为两个表{T1,T2}是无损分解:
- Eg.Head(T) = {X,Y,Z}, Head(T1) = {X,Y}, Head(T2) = {Y, Z}, Head(T1) 交 Head(T2) = {Y} -> Head(T1)/Head(T2)
4.2.1. 无损分解的例子

- T1∩T2 = {A} -> {A, B}(T1)
- T1∩T2 = {A} -> {A, C}(T2)
- T1∩T2 = {B} -> 无
- T1∩T2 = {C} -> 无

- PPT 157-158页
4.3. 有损分解
- 如果对于T的任何将来可能的内容,F中的函数依赖集保证满足以下关系,则将表T与函数依赖集的关联集F的分解称为有损分解:T 包含于 T1 join T2 join … join Tk
4.4. 数据库模式
- 数据库模式是数据库中所有表的标题集,以及设计人员希望保留在这些表的联接上的所有函数依赖的集。
- 所有不满足函数依赖的插入、更新等操作都会被拒绝。
4.5. 依赖保持性(FD Preserved)
- 给定具有通用表T和一组功能依赖项F的数据库模式,令{T1,T2,…,Tk}是T的无损分解。
- 然后,如果分解的某个表Ti为X∪Y包含于Head(Ti),则称F的函数依赖 X→Y被保留在T的分解中,或者T的分解被保存为函数依赖X->Y。
- 在这种情况下,我们认为函数依赖X->Y保留在Ti中或位于Ti或Ti中。
- 如果函数依赖集F和(F1∪F2∪…∪Fk)是相互等价的,即F+= (F1∪F2∪…∪Fk)+,则我们称该分解是具有依赖保持性的
4.6. 超键和超键查找算法
- 我们给出一个有函数依赖集F的表T,以及Head(T)上的属性集合为X:X是表T的超键 当且仅当 X 函数依赖上能够决定T的所有属性(X -> Head(T) or )
4.6.1. 超键查找算法
- 查找算法:每次检验少一个属性的可以不可以(找到没有必要的属性)

4.6.2. 超键查找算法的例子



4.7. 主属性
- 在表T中,一个属性A称为主属性当且仅当属性A存在于这个表的某个键K中。
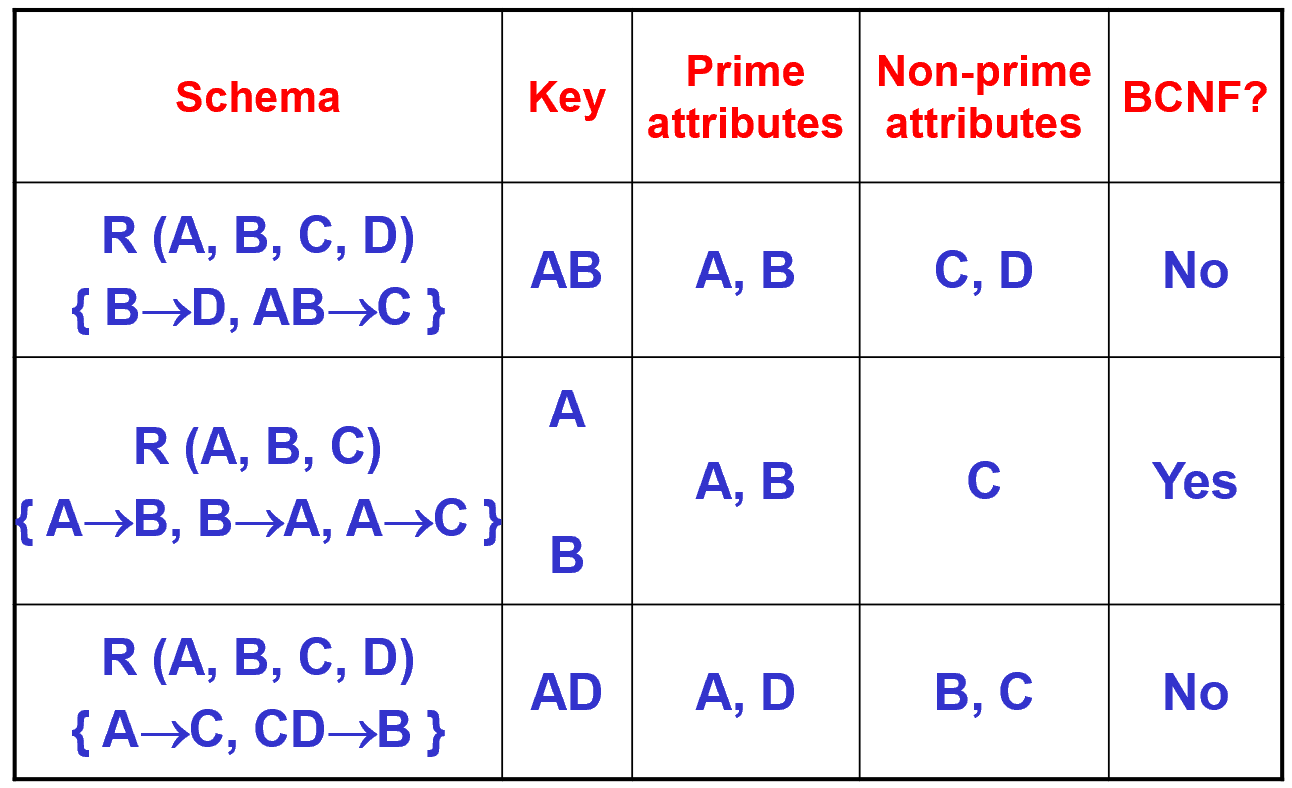
5. 范式
5.1. 范式BCNF
- 在数据库模式上的表T上有一个函数依赖集F满足BCNF 当且仅当 在任何F可推导出的任何一个满足如下两个条件的函数依赖X->A都在T中
- A是一个不在X中的单一属性
- X必须是T的超键。
- 所有表都满足BCNF,则数据库满足BCNF
- BCNF表示这个表没有属性被这个键集合的子集或者任何不包含这个键集合的不同属性集合函数决定。
- 判断BCNF的一种重要的方式,就是当前表上是否有更小可分解的依赖(小于全集)。
- 百度:BCNF条件
- 所有非主属性对每一个候选键都是完全函数依赖;(完全函数依赖(Full functional dependency):在一个关系中,若某个非主属性数据项依赖于全部关键字称之为完全函数依赖。)
- 所有的主属性对每一个不包含它的候选键,也是完全函数依赖;
- 没有任何属性完全函数依赖于非候选键的任何一组属性。

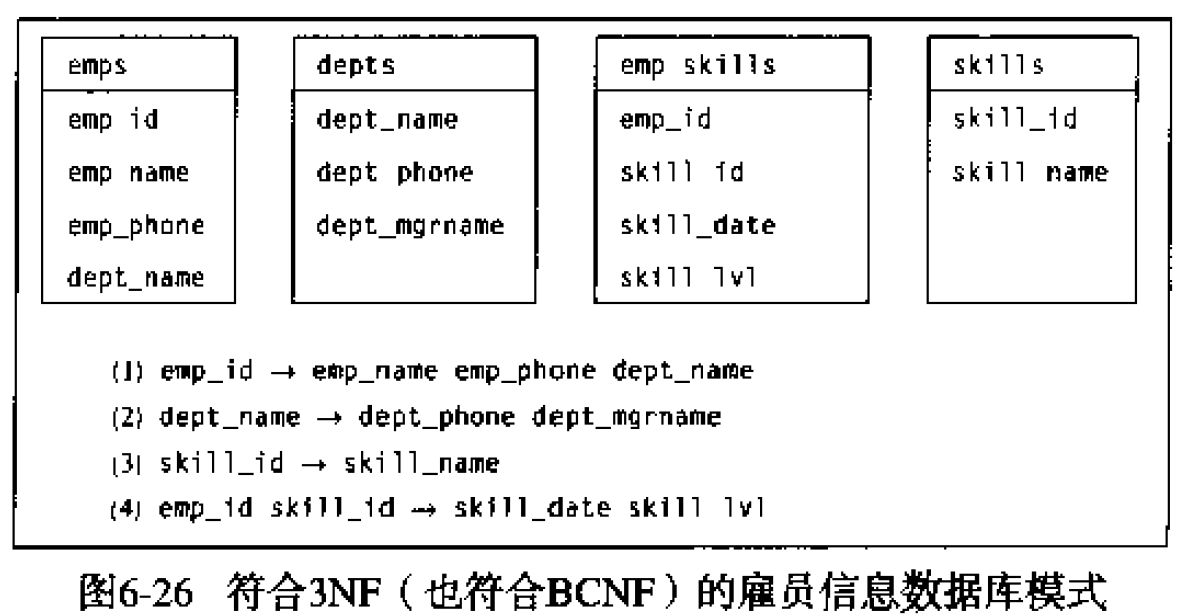
5.1.1. BCNF分解算法
- 首选求出最小依赖集合
- 找到候选键,合并成子集
- 然后检查函数依赖左侧是不是都是候选键

5.1.2. 将3NF分解为BCNF的例子

5.2. 范式3NF
- 在数据库模式上的表T上有一个函数依赖集F满足3NF 当且仅当 在F推导出的的任何一个在T上的函数依赖X->A(A是单个属性且不再X中),都满足如下2个条件之一:
- X是T的一个超键(也就是X->Head(T))
- A是T的一个主属性
- 所有的表都满足3NF,则称数据库满足3NF
- 例子:课本285页
5.2.1. 进行3NF的算法
- 给定通用表T和FD集F的情况下,该算法会生成3NF中的T的无损连接分解,并保留F的所有FD。
- 首先,将F替换成F的最小覆盖。
- S = 空集
- 对F中的所有X->Y
- 如果对全部Z属于S,X并Y不包含于Z,则S = S 并 Head(X 并 Y)
- 如果对T的全部候选键K
- 对Z全部的Z属于S,K不包含于Z
- 选择候选键K,S = S 并 Head(K)
- 输出是最终数据库模式中表的标题集S(属性集)。

- 算法的核心过程:R(ABCDE), F={A ->D,E->D,D->B,BC->D,DC->A},求保持函数依赖的3NF|具有无损连接性及保持函数依赖的3NF连接
- 首先求出最小函数依赖集合:
F={A->D,E->D,D->B,BC->D,DC->A} - 检查有没有没有出现在两侧的元素(如果有需要单独添加一个集合),之后合并得到3NF:
{AD} {ED} {DB} {BCD} {DCA} - 如果想要找到无损连接,我们通过找没有出现在依赖右侧和两侧均未出现的元素求得:
{AD} {ED} {DB} {BCD} {DCA} {CE},候选码是{CE}
- 首先求出最小函数依赖集合:
- 注意范式分解不唯一
5.2.2. 进行3NF分解的例子

5.2.3. 进行3NF分解的例子二



5.3. 范式2NF
- 在数据库模式上的表T上有一个函数依赖集F满足2NF 当且仅当 在F可推导出的任何一个满足如下条件的函数依赖X->A都在T上
- A是一个不在X中的单一非主属性
- X不是T的任何键K的真子集
5.4. 范式1NF
- 指数据库表的每一列都是不可分割的基本数据项,即实体中的某个属性不能有多个值或者不能有重复的属性。
5.5. 其他性质
- BCNF一定是3NF
- 3NF不一定是BCNF
2020-数据管理基础-ch06-数据库设计
https://spricoder.github.io/2020/07/03/2020-Fundamentals-of-Data-Management/2020-Fundamentals-of-Data-Management-ch06-%E6%95%B0%E6%8D%AE%E5%BA%93%E8%AE%BE%E8%AE%A1/