2019-数据结构-数据结构4-Tree
4 Tree
1. Tree 树
- 定义: A tree T is a collection of nodes(element). 树T是结点的集合
- The collection can be empty; otherwise, a tree consists of a distinguished node r, called the root, and zero or more nonempty(sub)trees T1, T2, ……, Tk(这个集合可能为空,否则这个树是由一个特殊的根节点和0个或多个子树组成)
1.1. 树的一些定义
- Degree of an elements(node) 节点的度数:有多少个子节点
- Degree of a tree 树的度:树里面结点的最大的度数。
- Leaf 叶节点:树里面度数为0的节点。
- Branch 分支节点:树里面度数不为0的节点。
- Level 层:各节点的层次为0或1,节点的层次等于其父结点的层次+1
- 树的高度:所有节点的最大层次数。
2. 二叉树
-
二叉树的定义:A binary tree t is a finite (possibly empty) collection of elements.(二叉树 t 是一个有限的节点的集合)
-
二叉树的特点:
- 二叉树的每个结点的度数为2
- 如果有子树,则子树均为二叉树,并且被称为左子树和右子树。
- 二叉树的左右子树是有区别的
2.1. 二叉树的应用
- 运算式的计算:转化成语法树后自带括号(运算次序)
2.2. 二叉树的性质(考前重点)
- n个结点的二叉树之间有n-1条边。
- 第i层的节点数最多是2i个
- 高度为h(从0开始计)的二叉树中结点最少h+1个,最多2h+1-1
- 如果一颗二叉树有n0个树叶,并且结点度数为2的节点有n2个,则n0=n2+1个
- 证明:设度数为1的节点为n1,则n=n0+n1+n2
- n = B + 1,B为分支数(总节点数 = 边数 + 1)
- B = 1 * n1+ 2 * n2
- 不会证明用数学归纳法
- 有n个结点的二叉树的高度最大为n-1,最小为log2(n+1)(向上取整)-1
2.3. 满二叉树
- 将二叉树排满,也就是如果高度为n的树,其节点数为2n+1-1个
2.3.1. 完全二叉树
- 定义:Suppose we number the elements in a full binary tree of height h using the number 1 through 2h+1(假设我们为一个高度为h的满二叉树进行使用1 - 2h+1的数字进行编码)
- We began at level 0 and go down to level h.Within levels the elements are numbered left to right. (我们从0层到h层,从左向右进行编码)
- 从上到下,从左到右进行编码
- 性质六: Let i, 0 <= i <= n-1,be the number assigned to an element of a complete binary tree. The following are true.(假设i,1<=i<=n-1,是一个确定二叉树的一个节点的编号)
-
- if i=0, then this element is the root of the binary tree. if i>0,then the parent of this element has been assigned the number (i-1)/2(向下取整)(如果i=0,则是根节点,不然其父结点的编号为 (i-1)/2(向下取整))
-
- if 2i+1 >= n,then this element has no left child. Otherwise,its left child has been assigned the number **2i+1**.(如果2*i+1>=n,那么这个元素没有左子女,不然左子女的编号就是这个数字)
-
- if 2i+2>=n, then this element has no right child, Otherwise its right child has been assigned the number **2i+2**.(如果2*i+2>=n,那么这个元素没有右子女,不然右子女的编号就是这个数字)
-
- 完全二叉树和满二叉树是不同的,完全二叉树的最后一层可以不全满,但是必须从左开始顺序无空缺。
2.4. 物理实现二叉树
2.4.1. 数组实现二叉树
- 其标记为其在数组中的下标,使用数组来存储。
- 常规二叉树的数组表示的位置上一定有空的。
- 很稀疏的二叉树会导致数组存储二叉树有大量的内存空间被浪费掉。
2.4.2. 链表实现二叉树
- Linked representation( also called L-R linked storage) 也被称为L-R链表存储。

- 二叉树节点
1 | |
- 二叉树
1 | |
- 正常二叉树操作
- In this class ,we employ a linked representation for binary trees.在这个class中我们使用链表来代表二叉树
- The function visit is used as parameter to the traversal methods,so that different operations can be implemented easily 函数visit被用作遍历方法的一个参数所以我们可以实现不同的操作更加简单
2.4.3. 链表具体实现方法细节
- 补充C++知识:
- Class::f()实现Class中的f()方法
1 | |
- 二叉树的应用
1 | |
2.5. 二叉树遍历
- 以下算法中的二叉树是通过链表实现的。
- Each element is visited exactly once
- V-----表示访问一个结点 vertice
- L-----表示访问V的左子树 left tree
- R-----表示访问V的右子树 right tree
- 所有的遍历顺序:VLR\LVR、LRV、VRL、RVL、RLV
- 常用的遍历顺序
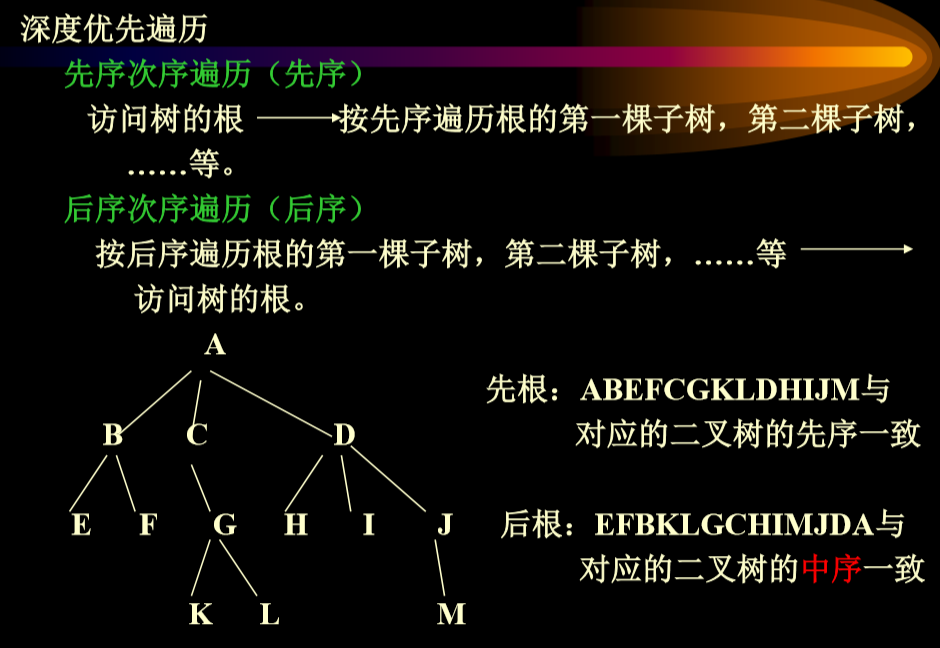
- 先序遍历:VLR
- 中序遍历:LVR
- 后序遍历:LRV
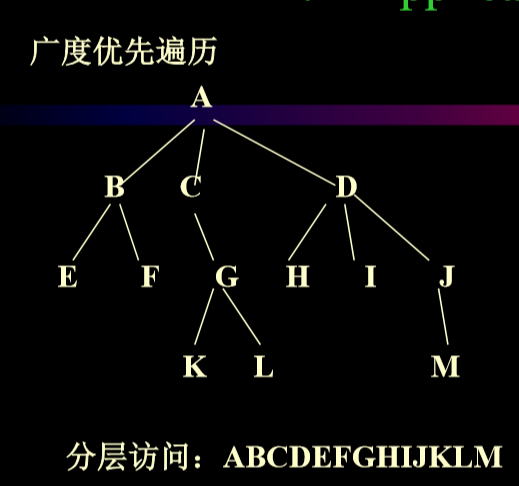
- 广度优先遍历:先处理树根节点,然后处理靠近的第一层的节点
2.5.1. 例子
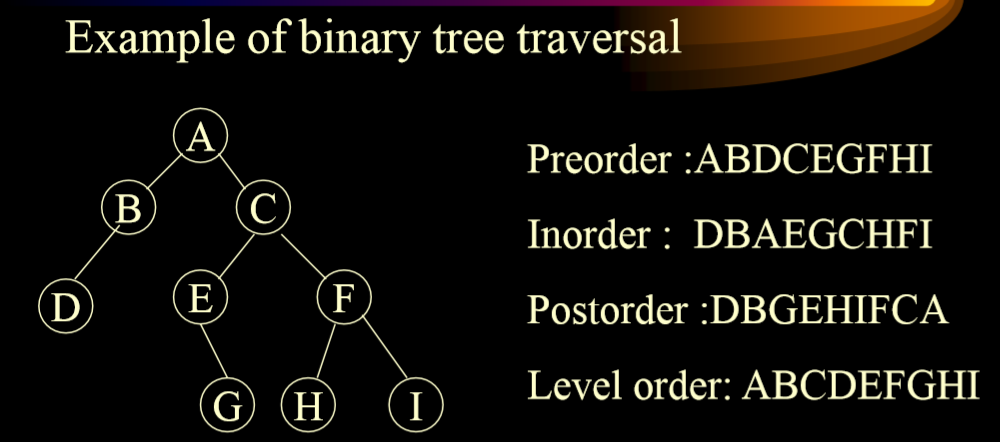
2.5.2. 先序遍历
- VLR
1 | |
2.5.3. 中序遍历
1 | |
2.5.4. 后序遍历
1 | |
2.5.5. 广度优先遍历
- 根据level order(树的层数)
数组实现
- 直接按顺序访问数组即可
链表实现
1 | |
2.6. 建立二叉树
2.6.1. 利用MakeTree函数
2.6.2. 利用先序、中序唯一的构造一颗二叉树
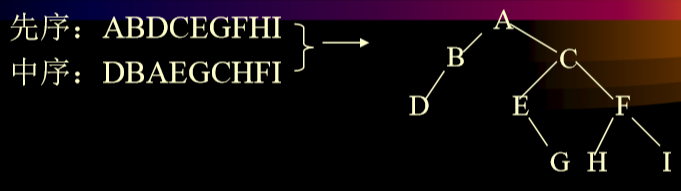
2.6.3. 利用二叉树的中序、后序遍历确定一颗二叉树
后序的最后是根节点,根据中序进行划分
2.6.4. 利用二叉树的广义表来构造一颗二叉树
2.6.5. 利用二叉树的后缀表示来构造一颗二叉树
2.6.6. 利用二叉树的后缀表示来构造一颗二叉树
3. 精讲:利用先序、中序唯一的构造一颗二叉树(string)
- 字符串(简称串)的定义以及一些术语
- 串:是n(n>=0)个字符的一个有限序列,开头结尾用双引号""括起来。
- 串的长度:串中所包含的字符个数n(不包括分界符‘ " ’,也不包括串的结束符‘\0’)
- 空串:长度为0的串。或者说只包含串结束符‘\0’的串,空串不等同于空白串。
- 子串:串中任一连续子序列
3.1. 其他的二叉树的方法
- PreOutput():output the data fields in preorder
- InOutput():output the data fields in inorder
- PostOutput():output the data fields in postorder
- LevelOutput():output the data fields in level order
- Delete():delete a binary tree,freeing up its nodes
- Height():return the tree height
- Size():return the number of nodes in the tree
- The height of the tree is determined as: max{hl, hr}+1
1 | |
3.2. String
1 | |
3.3. String部分方法的实现
1 | |
3.4. 根据先序遍历和中序遍历生成二叉树的思路
- 先序遍历的第一个一定是树根,然后在中序遍历中找树根,然后在中序中树根左边是左子树,右边是右子树
3.5. C++实现
1 | |
3.6. 已知其他的遍历顺序来生成二叉树
3.6.1. 已知后序遍历和中序遍历
- 先序遍历的树根在头部,而后序遍历串的树根在尾部。
3.6.2. 已知先序遍历和后续遍历串
- 先序遍历串的第二个位置是左子树(左右子树分界点),然后我们和后序遍历串结合。
3.7. 二叉树的应用
3.7.1. 二叉树的表示方式
- Binary-Tree Representation of a Tree 树的存储方式:三种
- 广义表表示:a(b(f,g),c,d(h,i,j),e)
- 双亲表示法;记下自己的父结点位置,问题是:找子节点需要遍历一遍。
- 左子女—右兄弟表示法
!(img/cpt5/4.png)
1 | |
3.7.2. 将森林转换成二叉树
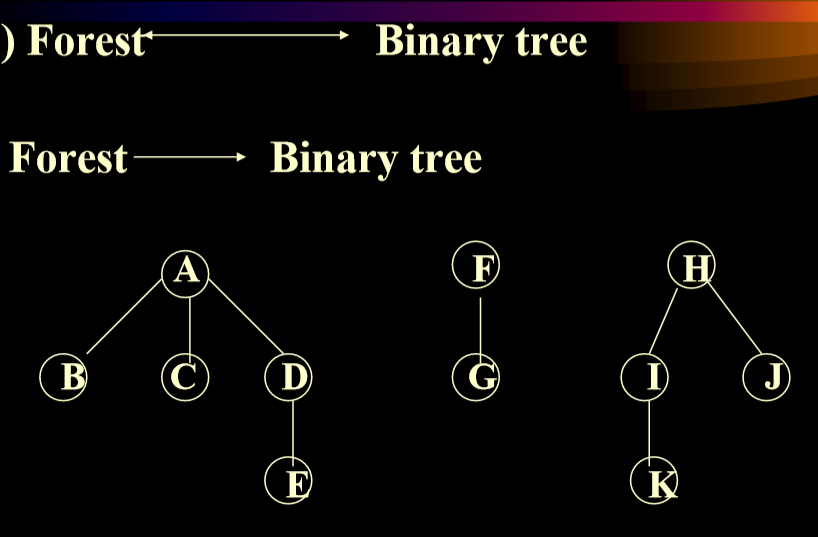
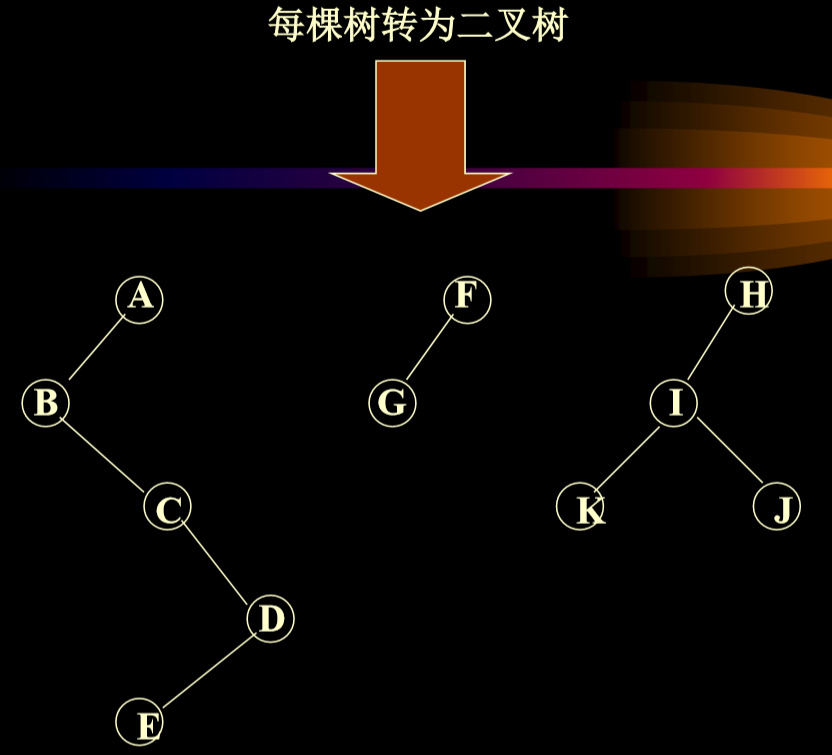
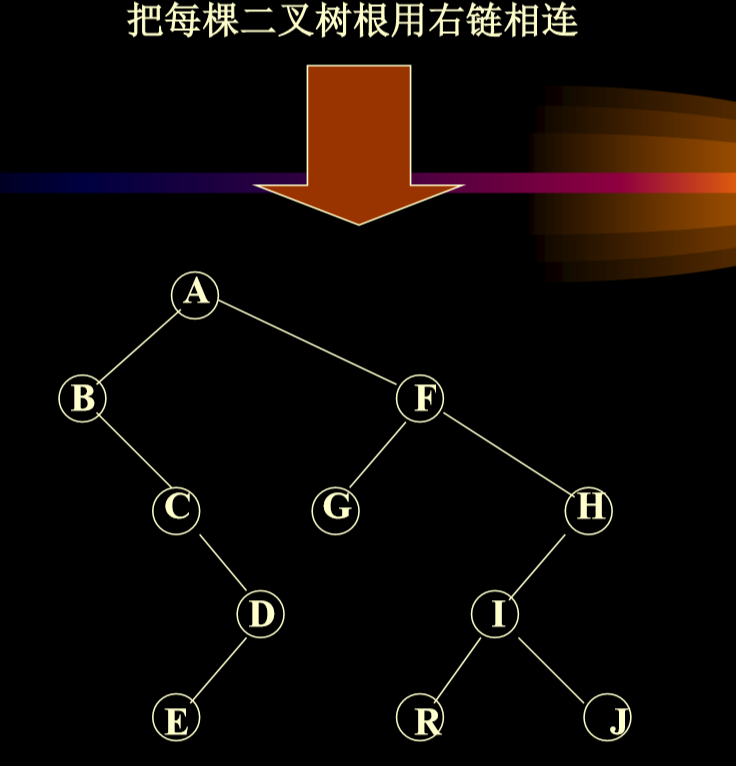
3.8. 树的遍历
3.8.1. 深度优先遍历(DFS)
3.8.2. 广度优先遍历
3.9. 森林的遍历
- 应用左子女-右兄弟的二叉树进行遍历
3.9.1. 深度优先遍历
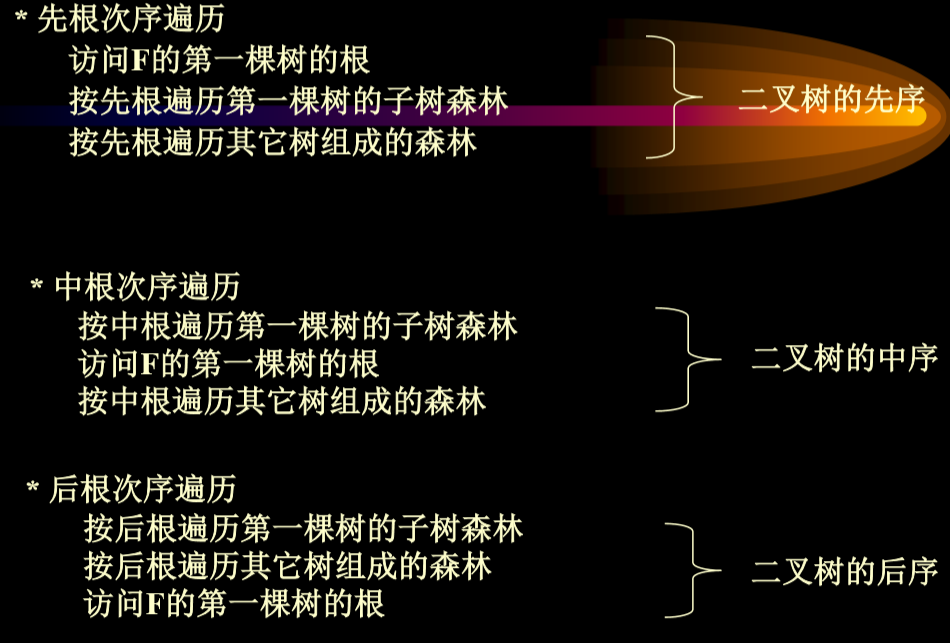
- Eg.
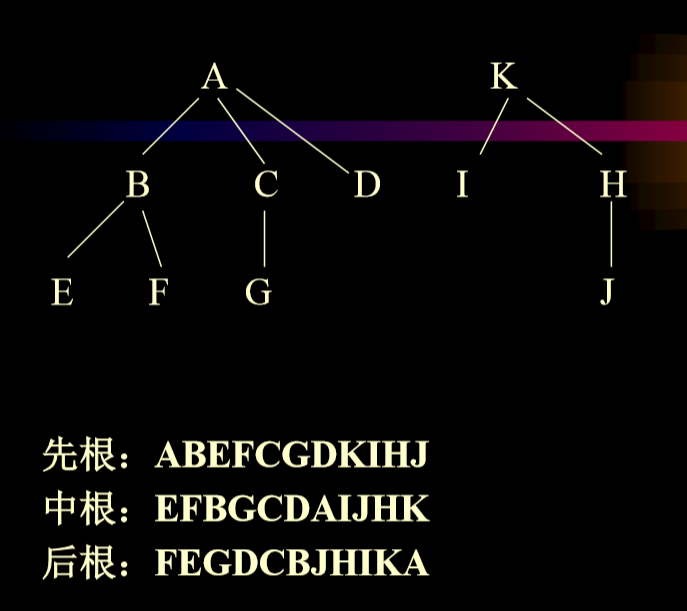
- 生成左子女-右兄弟二叉树后正常遍历即可
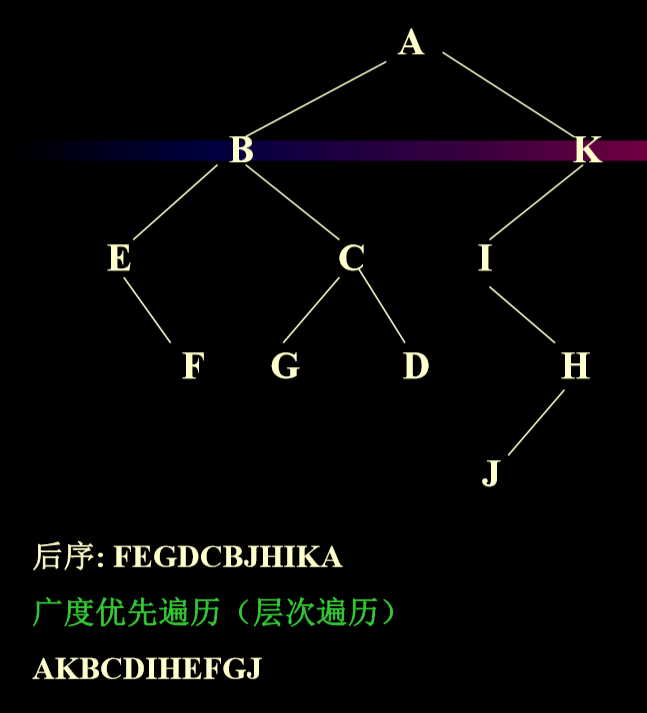
4. 线索二叉树
- 目的:让二叉树遍历的速度更快
- 特点:在树的节点中加入一个指针(比如指向下一个节点)
- n个结点的二叉树有2n个链域,其中真正有用的是n–1个,其它n+1个都是空域(null)。为了充分利用结点中的空域,使得对某些运算更快,如前驱或后继等运算。
4.1. 例子
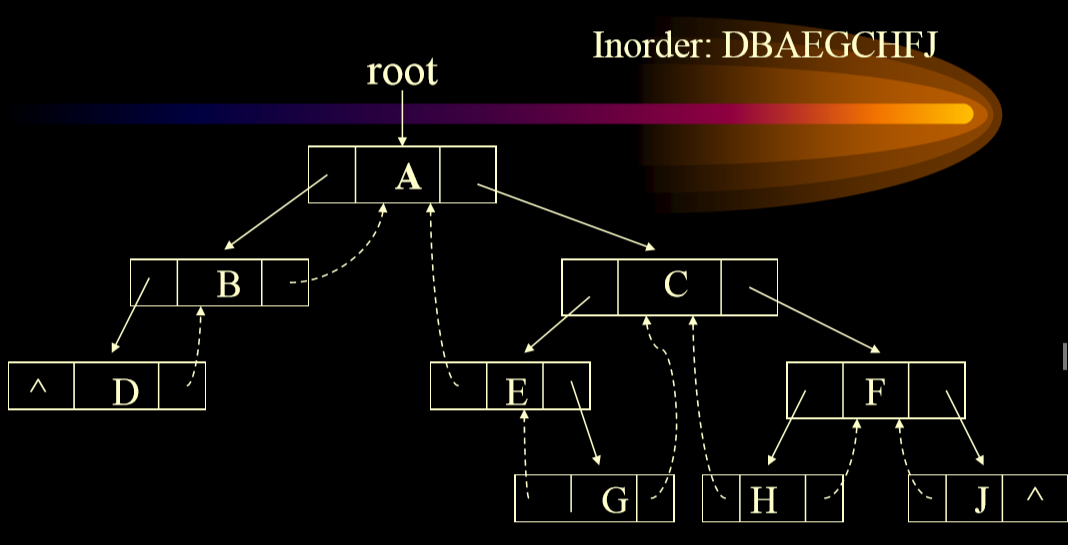
- 虚线是本身被置为NULL的部分
- 使用左指针指向中序遍历前项,使用右指针指向中序遍历的后项。
- 唯二空指针:最左边节点的左指针,最右边节点的右指针
- 整个树只会有两个空指针
4.2. 线索二叉树的结点的数据结构

4.3. 线索二叉树类的实现
1 | |
4.4. 中序遍历已有的中序线索二叉树
-
按中序遍历中序线索树
- 遍历算法(以中序为例):
- 递归, 非递归(需用工作栈)
- 这里前提是中序线索树, 所以既不要递归, 也不要栈。
- 遍历算法:
- 找到中序下的第一个结点(first)
- 不断找后继(Next)
- 如何找后继?
- 遍历算法(以中序为例):
-
情况一:如果p结点没有右子树(p->rightthread == 1)则 p=p->rightchild(右链就是后继)
-
p有右子树(p->rightThread==0) 则
- p=p->rightchild
- while(p->leftThread==0) p=p->leftchild;
1 | |
4.5. 建立中序线索二叉树
- 对已存在的一棵二叉树建立中序线索树
- 分析:与中序遍历算法差不多,但是要填左空域,右空域的前驱、后继指针。所以除了流动指针p外,还要加一个pre指针,它总是指向遍历指针p的中序下的前驱结点。
- pre相当于记录下来整个遍历顺序来完成链接
- Eg.
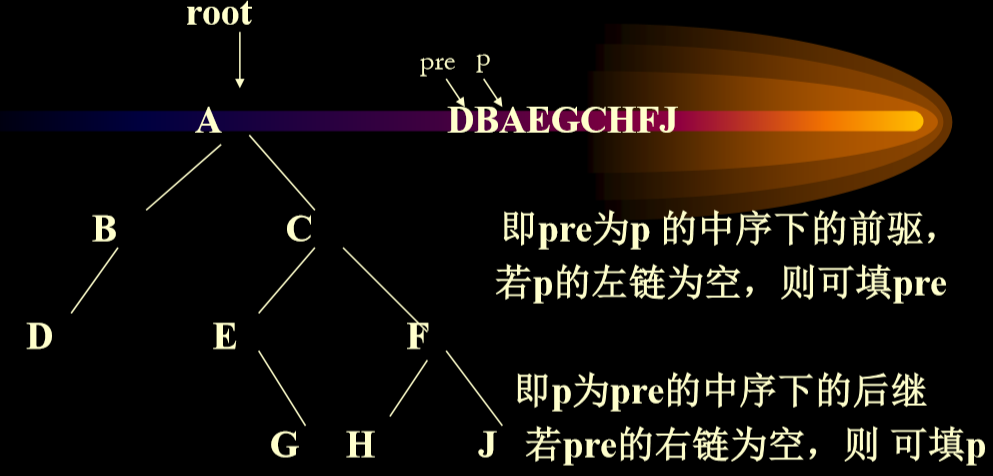
1 | |
5. 树的应用
5.1. 哈夫曼树(Huffman Tree)
5.1.1. 一些概念
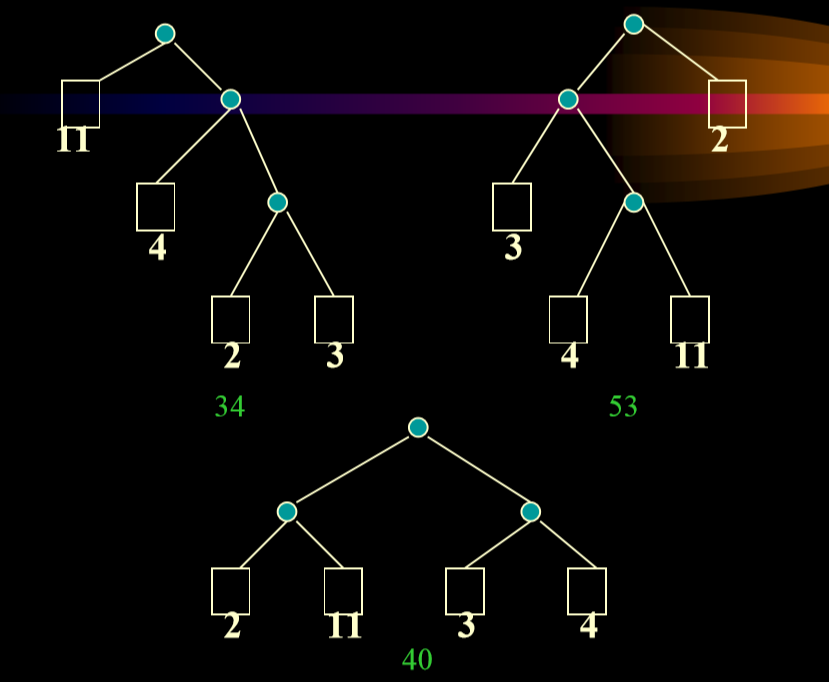
- 增长树(使得原来的树的每一个度数都为2)
- 对原二叉树中度为1的结点,增加一个空树叶
- 对原二叉树中的树叶,增加两个空树叶
- 外通路长度(外路径)E 根到每个外结点(增长树的叶子)的路径长度的总和(边数)
- E = 3+3+2+3+4+4+3+3=25,如右上图例
- 内通路长度(内路径)I:根到每个内结点(非叶子)的路径长度的总和(边数)。原来的树上每一个节点到树根的长度的综合
- I=2+1+0+3+2+2+1=11 如右上图例
- 结点的带权路径长度:一个结点的权值与结点的路径长度的乘积。
- 每个结点的权重占有一定的值
- 带权的外路径长度:各叶结点的带权路径长度之和。
- 带权的内路径长度:各非叶结点的带权路径长度之和。

例子如下
- 从形状上来讲,二叉树有以上三种大致形状。
5.1.2. Huffman算法
- 思想:权大的外结点靠近根,权小的远离根。
- 算法:从m个权值中找出两个最小值W1,W2构成

- 就是把计算结果放进去和其他节点一起选出两个,进行迭代
- 所以我们就是把数字比较大的挂到距离根比较近的地方
- 内节点不会只有一个叶节点。
5.1.3. 霍夫曼编码
- 是霍夫曼树在数据编码中一种应用。具体的讲用于通信的二进制编码中。设一电文出现的字符为D={M,S,T,A,Q, K},每个字符出现的频率为W={10,29,4,8,15,7},如何对上面的诸字符进行二进制编码,使得
- 该电文的总长度最短。
- 为了译码,任一字符的编码不应是另一字符的编码的前缀
- 根据树情况,我们知道编码是不具有二义性的,必然唯一对应,一个叶节点就一个结果
6. 考研例题
6.1. 2019年
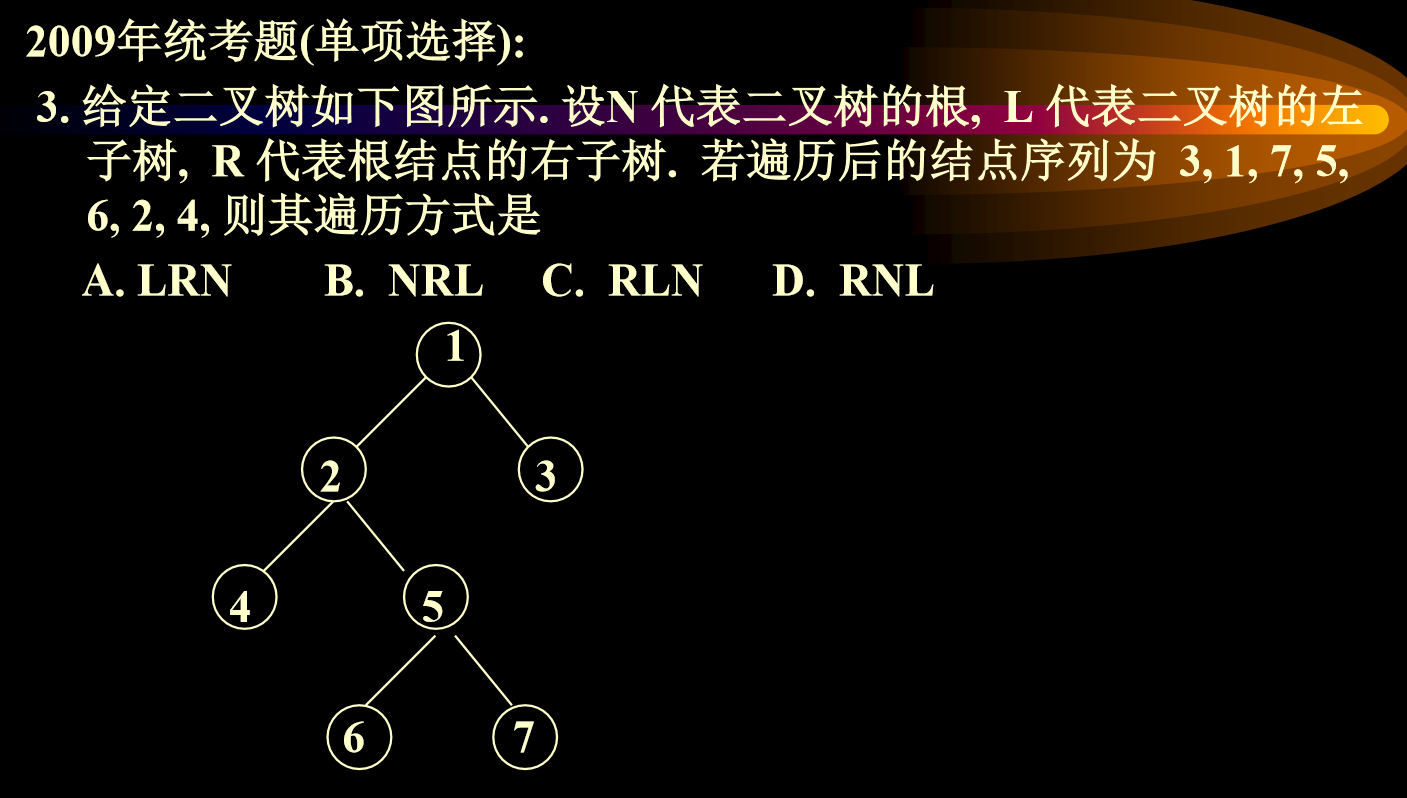
- D

- 4题:C 48+63(第六层:8个叶节点+24个根节点)
- 5题:B 左子女右兄弟,枚举法,v有四种情况,按照左子女右兄弟即可
- 最左边:不是父子也不是兄弟关系
- 第二个:父子
- 第三个:无关系
- 第四个:兄弟
6.2. 2020年
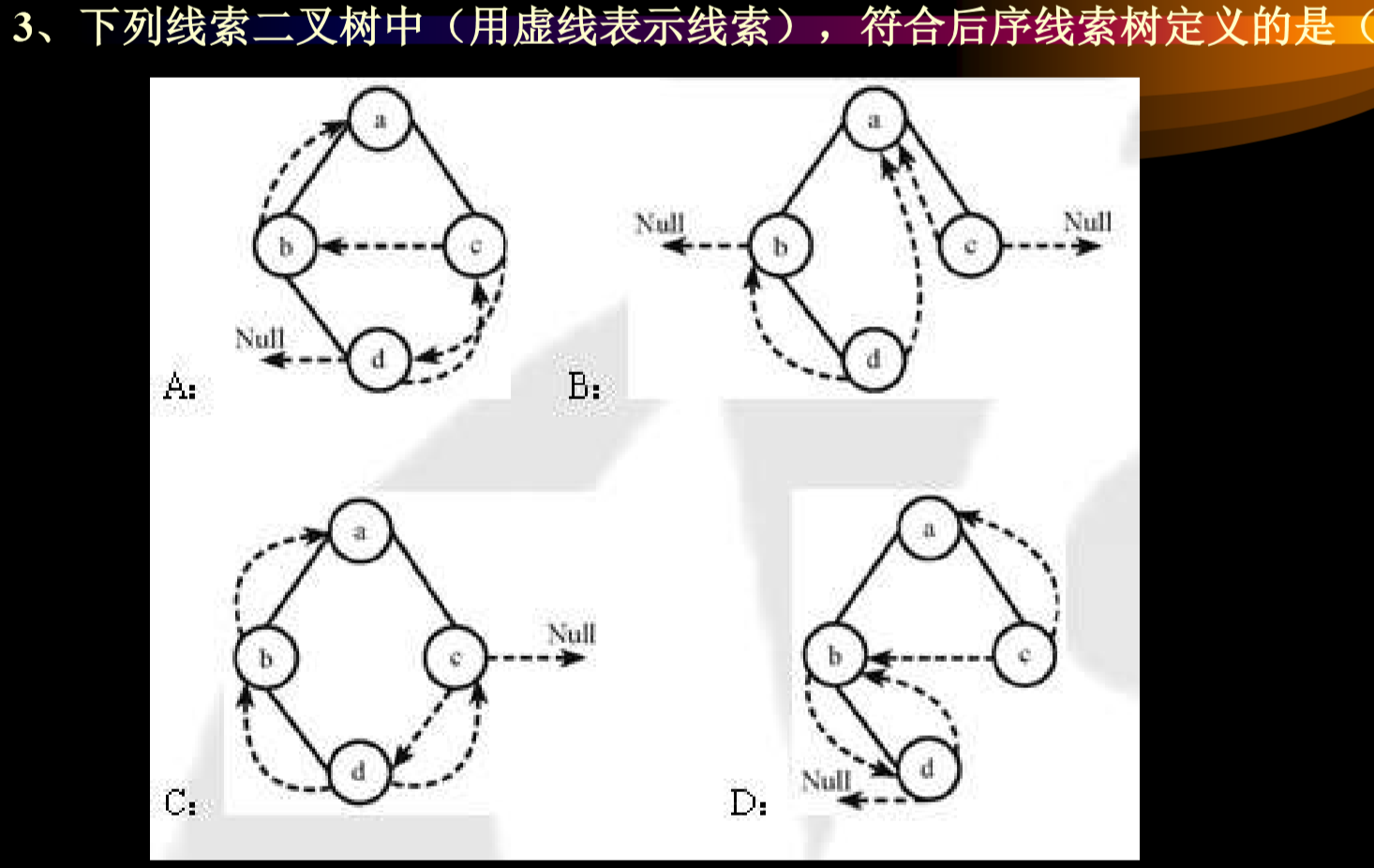
- 3题:D

- 5题:B
- 总结点数:204+103+12+101+1-(20+10+1+10)=82
- 6题:A
- 根节点度数可以为1,树中不含树根
7. 广义表
7.1. 广义表定义
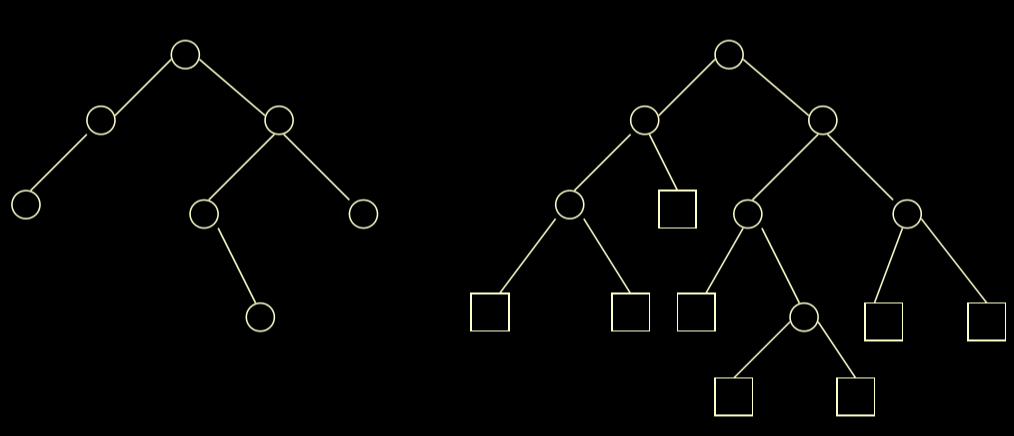
- 定义为n(n>=0)个表元素a0,a1,a2,……an-1组成的有限序列, 记作: LS=(a0,a1,a2,……an-1)
- 其中每个表元素ai可以是原子,也可以是子表.
- 原子: 某种类型的对象,在结构上不可分(用小写字母表示).
- 子表: 有结构的。(用大写字母表示)
- Eg.L = (3,(),(b,c),(((d))))
7.2. 广义表基础概念
- 长度:表中元素的个数
- 广义表的表头,表尾
- head= a0;
- tail= (a1, a2,……an-1)
- C=(a,(5,3,x)) 表头为a,表尾为((5,3,x))
- 广义表的深度:表中所含括号的最大层数
7.3. 广义表的性质
- 有序性
- 有长度,有深度
- 可递归,如上面例6
- 可共享,如E中B为E,D所共享
- 各种广义表都可用一种示意图来表示,用圆表示表元素, 用长方形表示原子

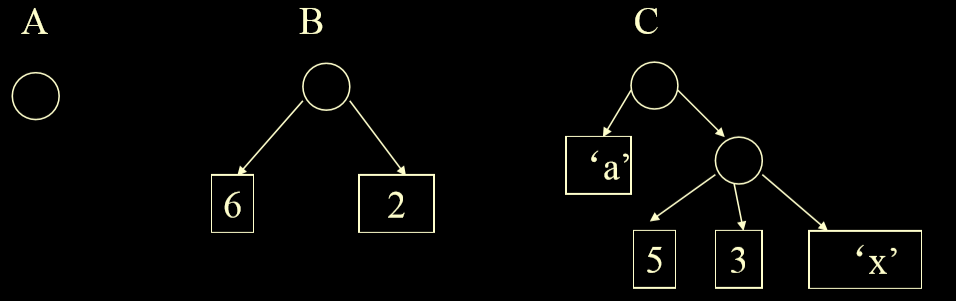
7.4. 广义表的操作

7.5. 广义表的实现

7.6. 广义表的类声明
1 | |
7.7. 广义表的实现

7.7.1. 求解广义表深度
1 | |
7.7.2. 判断两个广义表的相等关系
- 相等的条件: 具有相同的结构,对应的数据元素具有相等的值
1 | |
1 | |
7.7.3. 广义表的复制算法
- 分别复制表头,表尾,然后合成,前提是广义表不可以是共享表或递归表
1 | |
7.7.4. 广义表析构函数
1 | |
2019-数据结构-数据结构4-Tree
https://spricoder.github.io/2020/01/17/2019-Data-Structure/2019-Data-Structure-%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%844-Tree/