2019-数据结构-数据结构2-algrorithm Analysis

Algorithm Analysis(算法分析)
分析一个算法的时间和空间效率

1. 两个方法来进行算法分析

1.1. performance analysis

1.2. performance measurement

2. 空间复杂度(Space complexity)

  1. the amount of memory a program needs to run to completion 运行完成程序所需要的内存空间

2.1. 组件(components)

  1. 一个程序在电脑上运行时存储所需要的内存占用。

2.1.1. instruction space(指令空间)

  1. 这个是指程序编译成的二进制码的空间大小。
  2. 或者称为代码区，代码空间。
  3. 代码空间在某些情况下是不计算的:
    • 为什么:这部分和你的算法内容是无关的，更多的是系统对于二进制码的执行。
    • 同学们的源代码编译而成二进制码在载入内存时越大越大。这个对于不同软件的差异会很大。
    • 在windows里面的动态链接库就是用来处理这个问题，没必要一次性导入全部的二进制码。

2.1.2. data space(数据空间)

  1. space needed for constants,simple variables,component variables 常量、基本变量、成员变量所需的内存空间
  2. 数据区，主要是包括相应的数据等。各种变量常量的空间。

2.1.3. environment stack space(环境栈空间)

  1. to save information needed to resume execution of partially completed functions 保存恢复执行部分完成的函数所需的信息
  2. 栈空间、堆空间等。
    • 恢复执行程序功能而是用的空间。
    • 是一个比较细枝末节的空间。

2.1.4. 不计算的空间

  1. 操作系统的额外保留空间是不算的。(在计算算法复杂度的时候不考虑这个问题)

2.2. 空间复杂度讨论的数据区部分

2.2.1. a fixed part 定长部分

  1. include space for instructions,simple variables,fixed-size component variables,constants 包含指令、简单变量、定长度的成员变量、常量的内存空间
  2. 这部分空间是一定会存在的。
  3. 常数0所占据的空间也会算入。(但是是一个常数级空间)两个0怎么样呢?
    • 影响不大，因为怎么算都是常量级别的

2.2.2. a variable part 变量部分

  1. include space for component variables,dynamical allocated space,recursion stack 包含成员变量、动态分配空间、递归栈空间的内存空间部分
  2. 我们最关心的是这部分，也就是随着数据量的增长而带来的问题。

2.3. 算法例子

2.3.1. 例一

  1. 在调用相应函数之前的空间是不进行计算的，所以数组并没有单独多余输入。
  2. a是一个指针。

结果

  1. 例子机器是16个字节
  2. S(n):S表示space
  3. S(n) = 0:的含义是指占用空间是常数级的。
不同机器位数 每个int占据的大小 S(n)
16位 2 bytes 12 bytes
32位 4 bytes 24 bytes
64位 8 bytes 64 bytes

2.3.2. 例二

结果

  1. 只要你写了局部变量，局部变量静态分布，在执行局部之前就已经分配好了而不是等到执行的时候才分配地址。
  2. 返回值地址需要被存储(不然无法进行返回)

2.4. 为什么不是用空间增长率来表示空间复杂度

注意:S(n)并不是空间增长的导数。

3. 时间复杂度(Time complexity)

  1. the amount of time a program needs to run to completion 程序运行完成所需要的时间
  2. 编译时间是不计算近时间复杂度，一般来说我们的编译次数是远远小于运行时间，一般只消耗一次。

3.1. 计算程序的时间复杂度

  1. 关键的是计数中间的关键的操作个数。
    • 格外重要的是在循环中的操作个数
  2. 第一个例子:

  1. 先假设所有的操作都进行计算
    • 1(pos)+1(i)+(n-1)(for): 包含赋值语句，还包括for循环中每次都必须要做的语句。
    • 在循环中:首先进行条件判断，然后有一个可能做也可能不做的操作，然后是做i++，所以一个循环中最少是3倍，最多是4倍操作。
    • 所以操作数在(1+1+3(n-1)+1)-(1+1+4(n-1)+1)之间。
    • 不要太纠结这个非这个层次的操作个数
  2. 为什么计算时间复杂度比较模糊、很难精准表示?
    • 因为很多操作可能不止一个操作。
    • CPU执行不同指令的速度是不同的。

3.1.1. 补充：CPU和GPU的区别

  1. 在GPU中计算条件指令的速度很慢，但计算图形界面指令很快。而CPU则相反。
  2. GPU擅长负责图形(三维)、矩阵运算。
  3. CPU擅长运算数理逻辑。

3.1.2. 问题:我们需要计算到多么精细是合适的？

  1. 我们只需要做到时间复杂度的数量级即可。

3.2. 不同情况下的时间复杂度的情况

3.2.1. 最好情况

3.2.2. 平均情况

  1. 这个计算起来时很复杂的。
    • 其前提是所有情况的概率是一致的。
  2. 使用算术平均值来代替平均情况是一个简化的运算，在考试中是可以这么进行计算，但是并不能完全代表平均情况。

3.2.3. 最差情况

3.2.4. 例子

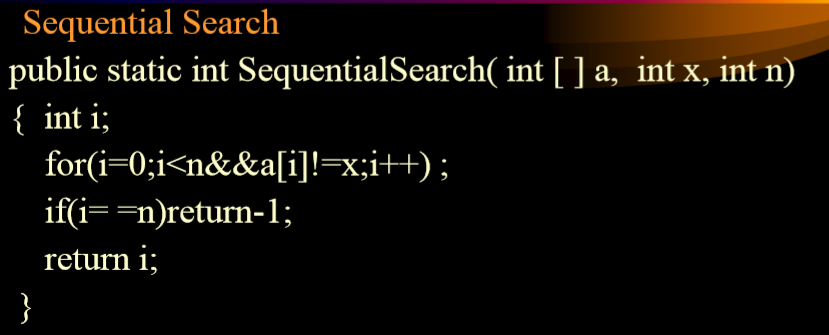
  1. 最好情况下:一次性结束，第一次找到
  2. 最坏情况下:n次结束，最后一次找到
  3. 平均情况下:(n+1)/2，使用算术平均值

  1. 不等概率下如何进行计算?
    • 将对应的位置上的概率加权进行计算。

4. 如何统计大规模的算法步数

  1. 使用整形变量count，并且加入到相应的必要的地方进行计数。
  2. 为程序加入计数器
  3. 第四个count是表示跳出的条件判断

5. 渐进性时间分析方法

  1. 我们更加关心的是文件规模比较大的情况下的算法时间复杂度问题。

5.1. 大O表示法

  1. provide a upper bound for the function f.表示函数 f 的上界
  2. 定义:f(n)=O(g(n)) iff positive constant c and n0 exist such that f(n) <=c * g(n) for all n, n>=n0
  3. 例子:

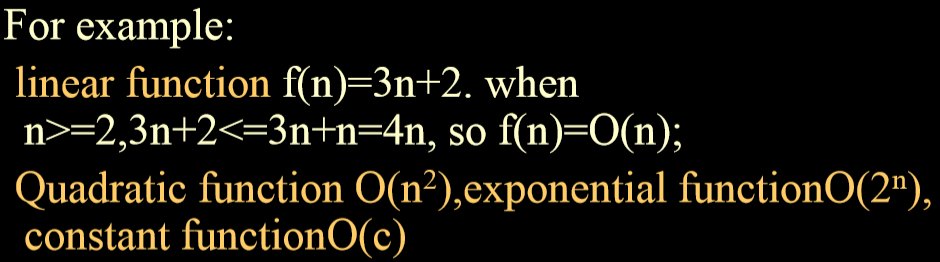
  1. 复杂度排序:从小到大
    1. O(1)
    2. O(log n)
    3. O(n)
    4. O(nlogn)
    5. O(n2)
    6. O(n3)
    7. O(2n)
    8. O(3n)
    9. O(n!)
    10. O(nn)
    11. O(nn...n)

5.1.1. 最大子序列的和

  1. MAXIMUM SUBSEQUNCE SUM PROBLEM 给定整数a1,a2,…,an (可能有负数)，求∑ak的最大值。
    • 求最大子序列和
  2. 算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
public static int maxSubSum1( int [] a ) {   
    int maxSum = 0; 
    for ( int i = 0; i < a.length; i++ )
        //双指针i和j卡两边，全遍历
        for ( int j = i; j < a.length; j++ ) {
            int thisSum = 0;
            for ( int k = i; k <= j; k++ ) 
                thisSum += a[k];
            if ( thisSum > maxSum )
                maxSum = thisSum;
        }
    return maxSum;
}
  1. 时间复杂度:O(n3)

算法优化

  1. 例子:通过前一个子序列加上之后的一个元素的和即为结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
public static int maxSubSum2( int [] a ) {   
    int maxSum = 0; 
    for( int i = 0; i < a.length; i++ ) {   
        int thisSum = 0; 
        for ( int j = i; j < a.length; j++ ) {
            //不从头加，进行累加
            thisSum += a[j]; 
            if ( thisSum > maxSum ) 
            maxSum = thisSum; 
        } 
    } 
    return maxSum; 
}

进一步的优化

  1. 我们使用分治法:将一个问题分为两个部分来解决。
  2. 分阶段:把问题分成两个大致相等的子问题，然后递归地对它们求解。
  3. 治阶段:将两个子问题的解合并到一起，可能在做些少量的附加工作，最后得到整个问题的解
  4. key:什么时候是两边都不是含有最大子序列的情况。
    • 如果是这样子的情况，那么左边的最右边和右边的最左边必定在这个序列中，通过生成法生成一个最大子序列。
    • 如果含有那么完成了优化。
  5. 优化代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
private static int maxSumRec( int [] a, int left, int right ) {   
    if ( left == right ) 
        if ( a[left] > 0 ) 
            return a[left];
        else  return 0;
    int center = ( left + right ) / 2;
    int maxLeftSum = maxSumRec( a, left, center );
    int maxRightSum = maxSumRec( a, center + 1, right );
    //向左生成局部最大子序列
    int maxLeftBorderSum = 0, leftBorderSum = 0;
    for ( int i = center; i >= left; i-- ) {
        leftBorderSum += a[i];
        if ( leftBordersum > maxLeftBorderSum )
            maxLeftBorderSum = leftBorderSum;
    }
    // 向右生成局部最大子序列
    int maxRightBorderSum = 0,rightBorderSum = 0; 
    for ( int i = center + 1; i <= right; i++ ) {
        rightBorderSum += a[i] ;
        if ( rightBorderSum > maxRightBorderSum )
            maxRightBorderSum =  rightBorderSum;
    }
    return max3( maxLeftSum, maxRightSun, maxLeftBorderSum + maxRightBorderSum );
    // 返回三者的最大值。
}
  1. 算法复杂度:O(nlog2n)
    • 先跳过去递归部分
    • for循环:两个for循环相当于遍历数组整整一遍。

算法复杂度 = 左递归 + 右递归 + O(n)
= 左左递归 + 左右递归 + 右左递归 + 右右递归 + 2 * O(n)
= …一共切(log2n)次
= O(log2n)*O(n)
= O(nlog2n)

5.1.2. 求最大公因数(GCD)

  1. 辗转相除法，用来求最大公因数。
1
2
3
4
5
6
7
8
public static long gcd( long m, long n ) {   
    while( n != 0 ) {    
        long rem = m % n; 
        m = n; 
        n = rem; 
    }
    return m;
}
  1. 分析最大公因数的算法复杂度
    1. 从逆向进推断:m1、m2、…、mn
    2. 前一个值等于后面一个值乘以商加上余数。也就是mi = p * mi+1 + mi+2
    3. 最坏情况下:p=1，p不可能为0。
      • 除了在一开始的情况下，p可能为0。
      • 最坏情况下是斐波那契数列。
      • 比如第一个数是一个亿，那么在最坏情况下我们就可以认为是斐波那契数列的第几项是一个亿。
    4. 复杂度是O(log N)，在1884年有一个精确的证明(By Lame)，也就是这个问题复杂度不会比斐波那契数列更差，转言之，斐波那契数列的算法复杂度是O(log N)

5.2. Omega Ω表示法

  1. 表示的是一个算法的复杂度在数量级上的下界。
  2. 定义:is the lower bound analog of the big Oh notation,permits us to bound the value f from below.

  1. 表示的是下限。

5.3. Theta θ表示法

  1. 不能向大了写，也不能向小了写。
  2. 考试中我们使用的表示法。
2019-数据结构
#课程笔记 #数据结构 #算法复杂度
2019-数据结构-数据结构2-algrorithm Analysis
https://spricoder.github.io/2020/01/17/2019-Data-Structure/2019-Data-Structure-%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%842-algrorithm%20Analysis/
作者
SpriCoder
发布于
2020年1月17日
许可协议