2019-计算机组织与结构-lecture10

lecture10 Error Correction

1. 错误(Error)

1. A semiconductor memory system is subject to errors(半导体系统容易导致错误)
2. Type(类型)
   1. Hard failure(硬件错误)
      • A permanent physical defect so that the memory cell or cells become stuck at 0 or 1 or switch erratically between 0 and 1(一种永久性的物理损坏，导致一个或多个存储单元卡在0或1上，或在0和1之间不稳定地切换)
      • Caused by harsh environmental abuse and manufacturing defects(由恶劣的环境滥用和制造缺陷造成硬件损坏)
   2. Soft failure(软件错误)
      • A random, nondestructive event that alters the contents of one or more memory cells without damaging the memory(一个随机的、非破坏性的事件可能改变一个或者更多的存储单元，而并不是破坏这些存储单元)
      • Caused by power supply problems or alpha particles(可能是由于电脑的电量问题或者alpha粒子等导致的问题)
3. 是发现哪一位错误更加困难，还是改正一个错误困难?
   • 发现错误更难，因为改正错误取反即可(因为只有0和1这两种状态)。

2. 错误修正(Error Correction)

1. Basic idea(基本观点)
   • Add some bits to store additional information for correction(添加一些位的数据来存储一些用于判断数据正误的额外信息)
2. Process(过程)
   • Data in(输入): produce a 𝐾 bits code 𝐶 on the 𝑀 bits data 𝐷 with a function 𝑓(原始数据D，其长度M，对其应用方法f生成额外信息C,其长度为K位，然后我们存储D和C)
   • Data out(输出): produce a new 𝐾 bits code 𝐶′′ on the data 𝐷′ with function 𝑓, and compare with the obtained 𝐾 bits code 𝐶′(根据新的取出来的D’，再次对其应用方法f得到新的额外信息C’’，和拿出来的C’进行比较。)
     • No error detected: send 𝐷′
     • An error detected which can be corrected: correct it and send 𝐷’’
     • An error detected which cannot be corrected: report
   • 注:我们可以认为方法f是不会出错的，为什么?因为如果f出错，作为一个程序，是无法正常运行的。
3. 额外信息C作为一个信息也可能是有可能出错的。
   • 存储的额外的信息不能够太大，不然成本太高。
4. 一旦存入C，拿出来的数据就是C’，而原来的C已经永远的消失了
   • 为什么？因为如果能拿到原来的C，那么以上所有的事情都没有意义。
5. 一切的假设前提:数据出错的频率是很低的
   • 也就是C和D同时出错是极小概率的。

2.1. 过程

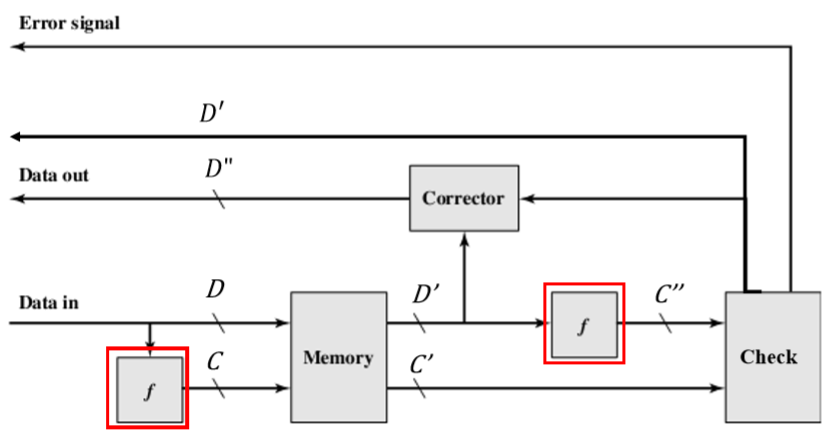
1. 一旦进入Memory中，C和D已经永远的消失了(再次强调)

2.2. Parity Checking(奇偶校验检查)

1. Basic idea(基本思想)
   • Add one bit to denote whether the number of 1 in data is odd or even(用一位的额外位来表示这个数据是奇数还是偶数)
2. Procedure(过程)
   1. Assume the data is 𝐷 = 𝐷_𝑀…𝐷₂𝐷₁
   2. Data in
      • Odd parity: 𝐶 = 𝐷_𝑀 ⊕ ⋯⊕ 𝐷₂⊕ 𝐷₁ ⊕ 1
      • Even parity: 𝐶 = 𝐷_𝑀 ⊕ ⋯⊕ 𝐷₂⊕ 𝐷₁
   3. Data out
      • Odd parity: 𝐶′′ = 𝐷′_𝑀 ⊕ ⋯⊕ 𝐷′₂⊕ 𝐷′₁⊕ 1
      • Even parity: 𝐶′′ = 𝐷′_𝑀 ⊕ ⋯⊕ 𝐷′₂⊕ 𝐷′₁
   • Check: S = 𝐶′′⊕ 𝐶′
     • 𝑆 = 1: the number of error bits is odd(有奇数个位置是错误的)
     • 𝑆 = 0: correct or the number of error bits is even(有偶数个位置是错误(正确)的，ps.也有可能本身没有出错)
     • 上面的位置错误的数字是C’’(D’)和C’中错误的位数的综合。
3. 对于偶校验:将新生成的C加入到原来的D的序列中,则其中的1的个数是偶数。
   • 如果原来的所有的D中有奇数个1，最后C为1，则添加C这一项之后的结果中有偶数个1。
   • 如果原来的所有的D中有偶数个1，最后C为0，则添加C这一项之后的结果中有偶数个1。
4. 对于奇校验:将新生成的C加入到原来的D的序列中，则其中的1的个数是奇数。
5. 对于错误信息的校验:前后的奇偶校验的类型必须一样
6. Advantage(奇偶校验法的优点):Low cost
7. Disadvantage(奇偶校验法的缺点)
   • Cannot find the errors when the number of error bits is even(如果错误的位数是偶数的话，我们是无法发现错误的)
   • Cannot be used for correction(只能检验出来哪里有错误，不能确定具体错误的是哪一位)
   • Suitable to check one byte data(相对比较适合检验一字节的数据)
8. 就校验比较适合用于比较短的01串。

2.3. 汉明码(Hamming Code)

1. Basic idea(基本思想)
   • Divide the bits into several groups, and use parity check code on each group for error correction(我们将数据分成很多组，对于每一组使用检查正误的奇偶校验码)
2. Procedure
   1. Divide the 𝑀 bits into 𝐾 groups(将M位数据划分成K个组)
   2. Data in: produce one bit for each group, and get a 𝐾 bits code(对于每一个分组生成一个奇偶校验码，一共获得了K个奇偶校验码)
   3. Data out: produce one bit for each group, and get a new 𝐾 bits code(根据当前每一组的数据获得新的一位奇偶校验码，获得一个新的K位的奇偶校验码)
   4. Check: produce 𝐾 bits code for fetched data, take the exclusive-OR of each bit of the produced code and fetched code, and produce 𝐾 bits syndrome word(根据取得的数据生成的K位的奇偶校验码，我们对取出来的奇偶校验码和刚生成的奇偶校验码进行异或操作，生成一个K位的故障字)
3. 优点:既可以见检查错误，也可以定位错误位置。

2.3.1. 汉明码的检查

1. Check code length(检查字的长度)
   • Assume at most one bit error occurs(假设大多数的情况下只会发生一位的错误)
   • Possible errors
     • One bit error in data: 𝑀种情况
     • One bit error in check code: 𝐾种情况
     • No error: 1种情况
2. Length of check code
   • 2^K ≥ 𝑀 + 𝐾 + 1
   • 满足上述式子:保证每一种情况可以被定位出来,这被用来求K位最小值

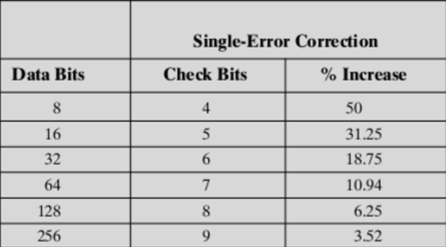
3. 为什么我们不能让汉明码特别长?
   • 因为一旦太长了，数据两位出错的概率会增加，二者就不符合之前的假设了。

2.3.2. 故障字的意义

1. Map each value of syndrome word to one possible situation(每一个故障字的值对应着一种情况)
2. Rule(规则)
   • All 0s: no error has been detected(如果故障字全是0:我们认为没有发生错误)
   • One bit is 1: an error has occurred in one of the check bits, and no correction is needed(如果故障字有一位为1:我们认为大概率是因为校验码出问题，并且我们不需要进行修改数据，为什么？因为数据出现问题影响的不止一位)
   • More than one bit is 1: the numerical value of the syndrome indicates the position of the data bit in error, and invert this data bit for correction(如果故障字超过1位为1:我们认为数据出现了问题，需要修正)
3. C’和C’'生成故障字。

2.3.3. 数据划分

1. Dada bits division(数据位数的划分)
   • Assume the 8 bits data is 𝐷 = 𝐷₈…𝐷₂𝐷₁, the 4 bits check code is 𝐶 = 𝐶₄𝐶₃𝐶₂𝐶₁(我们假设数据一共8位，根据之前我们可以知道故障字的长度为4)
   • Relationship of data bit / check code and syndrome word(数据/检查字和故障字之间的关系)

2. 生成的故障字为一个，我们认为是C’(检查字)有问题，而生成超过一个，我们认为是D’(数据)有问题
3. 对于故障字1011，假设C’和C是一致的，一开始D₇ 需要参与C_4,2,1 的计算，而不能参与C₃ 的计算
4. 故障字，按照其二进制值的大小排列，先写出来检查字的错误，再写出数据的错误，然后根据表格写出如何计算检查位。
   • 这个是在干什么？是根据和故障字之间的关系，推理出f的计算方法
5. Set the bit in the position with the same value of its syndrome word(所以我们把数据设置到和故障字的值相同的位置上)

2.3.4. 汉明码的例子

1. Assume the 8 bits data is 𝐷=01101010, and use even parity in producing hamming code(我们假设有一个8位数据为01101010，我们使用偶校验生成汉明码)
2. The code is(额外信息的码值如下)(根据其二进制有无这一位决定)
   • 𝐶1 = 𝐷1 ⊕ 𝐷2 ⊕ 𝐷4 ⊕ 𝐷5 ⊕ 𝐷7 = 0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 1 = 1
   • 𝐶2 = 𝐷1 ⊕ 𝐷3 ⊕ 𝐷4 ⊕ 𝐷6 ⊕ 𝐷7 = 0 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 1 = 1
   • 𝐶3 = 𝐷2 ⊕ 𝐷3 ⊕ 𝐷4 ⊕ 𝐷8 = 1 ⊕ 0 ⊕ 1 ⊕ 0 = 0
   • 𝐶4 = 𝐷5 ⊕ 𝐷6 ⊕ 𝐷7 ⊕ 𝐷8 = 0 ⊕ 1 ⊕ 1 ⊕ 0 = 0
3. The 12 bits content when store 01100101001****1
   • 所以我们的额外信息并不是随意加入到校验信息的后面的，而是加入到之前的对应表上的对应位置上，从而有力的保证了确定问题位置
   • 注意插入的应该是指定的位置

1. case1:正常情况下的S的值为0000
2. case2:第九位(1为基)出错，那么我们算得S为1001
3. case3:第八位(1为基)出错，那么我们算得S为1000

2.3.5. 汉明码的扩展

1. SEC
   • Single-Error-Correcting
   • Can find and correct one bit error(可以发现一位的错误，并且确定一位的错误的位置)
2. SEC-DED
   • Single-Error-Correcting, Double-Error-Detecting
   • Can find two bits error and check one bit error(我们可以发现两位的错误，并且确定一位的错误位置)
   • Add one additional bit
     • 𝐶5 = 𝐷1 ⊕ 𝐷2 ⊕ 𝐷3 ⊕ 𝐷5 ⊕ 𝐷6 ⊕ 𝐷8
   • If an error occurs in one bit data, three bits check code will be changed(如果一个错误出现在一位的数据中，那么三位的检查码会被改变)
   • 理论上不要求

SEC-DED的判断

1. All 0s: no error has been detected(如果故障字全为0，那么我们没有发现错误)
2. One bit is 1: an error has occurred in one of the 5 check bits, and no correction is needed(如果错误发生在5个检查位之一，那么我们认为是故障字出错，而并不是数据出现问题)
3. Two bits are 1: errors have occurred in two of data and check bits, but the positions of errors cannot be found(如果故障字中出现两个1，那么我们知道有两个位置发生了错误，但是无法定位)
4. Three bits are 1: an error has occurred in one of the 8 data bits, and the error can be corrected(如果故障字有三个1，那么我们知道在8位数据中出现了错误，并且我们可以获得错误的位置)
5. More than three bits are 1: serious situation, examine the hardware(如果有超过3个1，那么我们认为发生了很严重的情况，检查硬件状况)
6. 本部分中所有的位置均值数据和检查位的错误位之和。

SEC-DED的特点

1. An error-correcting code enhances the reliability of the memory at the cost of added complexity(纠错码以增加复杂度为代价提高了存储器的可靠性。)
2. The size of main memory is actually larger than is apparent to the user(主存储器的大小实际上比用户看到的要大得多)

3. CRC(Cyclic Redundancy Check循环冗余校验码)

3.1. 目前面临的问题

Problem of parity checking(奇偶校验法的问题)

• Additional cost is large(额外的代价比较大)
• Require to divide data into bytes(需要把数据切割到每一位)

3.2. 解决方案CRC

3.2.1. CRC的特点

1. Suitable for storing and transmitting large size data in stream format(适合以流格式存储和传输大数据)
2. Generate the relationship between data and check code with mathematic function(用数学函数生成数据与校验码之间的关系)

3.2.2. CRC的基本思想

1. Assume the data has 𝑛 bits, left shift the data(k位), and divide it (mod 2 operation) with a 𝑘 + 1 bits generator polynomial(生成多项式)(我们假设数据一共n位，左移数据k位，然后我们用之后的结果除以k+1位的生成多项式)
2. Use the 𝑘 bits remainder as the check code(使用k位余数作为校验码)
3. Put the check code behind the data(将校验码放到数据的后面，然后作为整个数据传入到存储器中去)

3.2.3. CRC的Check

1. If the 𝑛 + 𝑘 bits content can be divide by generator polynomial, no error occurs(如果我们用(n+k)位的存储的值除以生成多项式，那么没有问题产生)
2. Otherwise, errors occur

3.2.4. CRC的部分具体操作

1. 生成多项式有两种方法:
   1. 10010
   2. X⁴ + X
2. 将数据逻辑左移3(4-1)位
3. 做除法算校验码:摩尔除法
   • 摩尔除法的原理:使用异或,即保持目前的被除数的最高位和除数的最高位进行异或，得到的结果作为结果的高位。

CRC的例子

1. Assume the data is 100011, the generation polynomial is 1001(我们假设数据为100011，我们的生成多项式为1001(x³+1))
2. The check code is 111(结果校验码为111)

3. 最后存储的结果为100011 + 111